
Question and Answers Forum
Question Number 73649 by aliesam last updated on 14/Nov/19
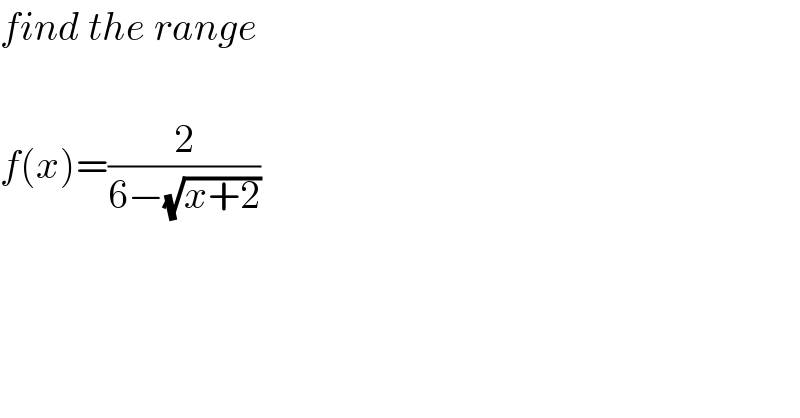
Commented by mathmax by abdo last updated on 14/Nov/19
![x ∈D_f ⇔ x≥−2 and (√(x+2))≠6 ⇔x≥−2 and x+2 ≠36 ⇔x≥−2 and x≠34 ⇒D_f =[−2,34[∪]34,+∞[ f^′ (x)=2(−((−(1/(2(√(x+2)))))/((6−(√(x+2)))^2 ))) =(1/((√(x+2))(6−(√(x+2)))^2 ))>0 ⇒f is increazing on D_(f ) we have f(−2)=(1/3) and lim_(x→34^− ) f(x) =+∞ lim_(x→34^+ ) f(x)=−∞ ⇒f([−2,34[)=[(1/3),+∞[ and f(]34,+∞[) =]−∞,0[ variation of f x −2 34 +∞ f^′ + ∣∣ + f (1/3) inc +∞∣∣−∞ inc 0](Q73691.png)
Commented by malwaan last updated on 14/Nov/19
![x≥−2 and x≠ 34 ⇒−2≤ x < 34 ∨ x > 34 −2≤ x < 34⇒0≤x+2<36 ⇒0≤(√(x+2)) <6⇒0≥−(√(x+2)) >−6 ⇒6≥6−(√(x+2)) >0 ⇒(1/3)≤ (2/(6−(√(x+2)))) < ∞ ⇒(1/3) ≤ y < ∞ ....(1) x > 34⇒34<x<∞ ⇒36< x+2 < ∞ ⇒6<(√(x+2)) <∞ ⇒−6>−(√(x+2)) >−∞ ⇒0>6−(√(x+2)) >−∞ ⇒−∞<(2/(6−(√(x+2)))) < 0 ⇒−∞<y<0 ....(2) from(1);(2) ⇒the range = [1 ╱ 3 ; ∞[ ∪ ]−∞ ; 0 [](Q73693.png)
Answered by MJS last updated on 14/Nov/19
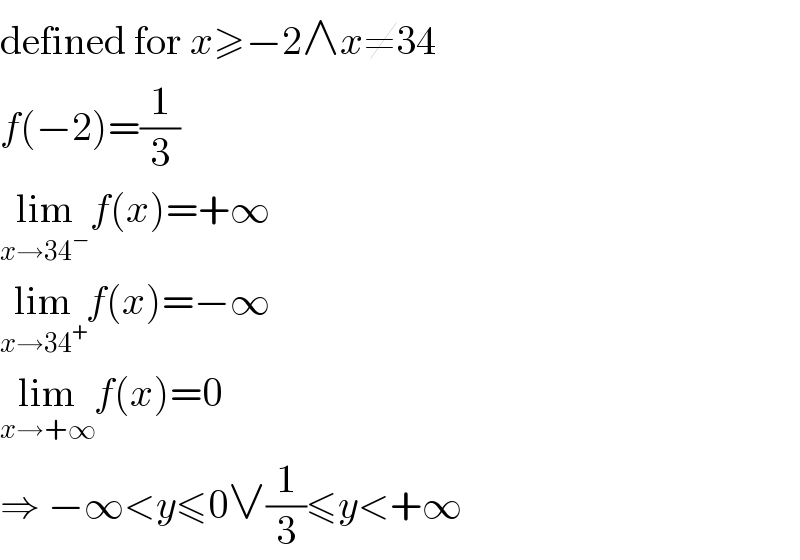
Commented by aliesam last updated on 14/Nov/19

Commented by aliesam last updated on 14/Nov/19

Commented by MJS last updated on 14/Nov/19

