Question Number 73751 by ~blr237~ last updated on 15/Nov/19
$${Find}\:\:{out}\:{the}\:{value}\:{of}\:\:\: \\ $$$$\:\:{J}=\int_{\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{2}{e}^{−\mathrm{2}{xy}} −{e}^{−{xy}} \right){dxdy}\: \\ $$
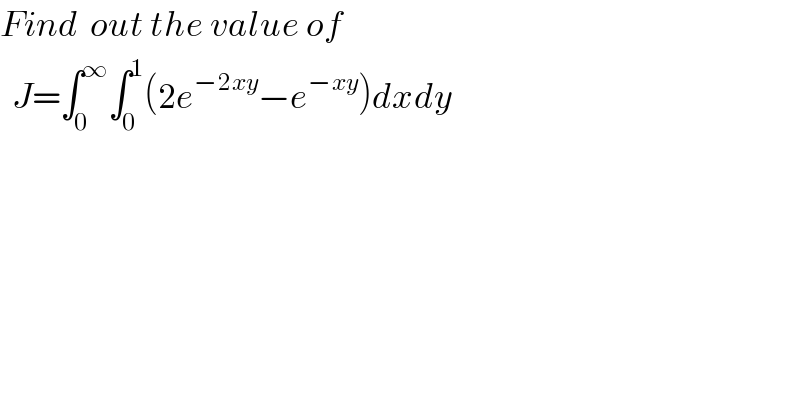
Commented by mathmax by abdo last updated on 15/Nov/19
![J =∫_0 ^∞ A(y)dy with A(y)=∫_0 ^1 (2 e^(−2xy) −e^(−xy) )dx ⇒ A(y)=[−(1/y)e^(−2xy) ]_(x=0) ^(x=1) −[−(1/y)e^(−xy) ]_(x=0) ^(x=1) =(1/y)(1−e^(−2y) )+(1/y)(e^(−y) −1) =(1/y)(1−e^(−2y) +e^(−y) −1)=((e^(−x) −e^(−2y) )/y) ⇒ J =∫_0 ^∞ ((e^(−y) −e^(−2y) )/y)dy let f(u)=∫_0 ^∞ ((e^(−y) −e^(−2y) )/y) e^(−yu) dy with u≥0 we have f^′ (u) =−∫_0 ^∞ (e^(−y) −e^(−2y) )e^(−yu) dy =∫_0 ^∞ (e^(−(u+2)y) −e^(−(u+1)y) )dy =[((−1)/(u+2))e^(−(u+2)y) +(1/(u+1))e^(−(u+1)y) ]_0 ^∞ =(1/(u+2))−(1/(u+1)) ⇒f(u) =ln∣((u+2)/(u+1))∣ +c due to the continuity ∃m>0 /∣f(u)∣≤m ∫_0 ^∞ e^(−yu) dy =(m/u) →0(u→+∞) ⇒c=0 ⇒f(u)=ln∣((u+2)/(u+1))∣ J=f(0) =ln∣(2/1)∣ =ln(2)](Q73799.png)
$${J}\:=\int_{\mathrm{0}} ^{\infty} {A}\left({y}\right){dy}\:\:{with}\:{A}\left({y}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{2}\:{e}^{−\mathrm{2}{xy}} −{e}^{−{xy}} \right){dx}\:\Rightarrow \\ $$$${A}\left({y}\right)=\left[−\frac{\mathrm{1}}{{y}}{e}^{−\mathrm{2}{xy}} \right]_{{x}=\mathrm{0}} ^{{x}=\mathrm{1}} \:−\left[−\frac{\mathrm{1}}{{y}}{e}^{−{xy}} \right]_{{x}=\mathrm{0}} ^{{x}=\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{{y}}\left(\mathrm{1}−{e}^{−\mathrm{2}{y}} \right)+\frac{\mathrm{1}}{{y}}\left({e}^{−{y}} −\mathrm{1}\right)\:=\frac{\mathrm{1}}{{y}}\left(\mathrm{1}−{e}^{−\mathrm{2}{y}} \:+{e}^{−{y}} −\mathrm{1}\right)=\frac{{e}^{−{x}} −{e}^{−\mathrm{2}{y}} }{{y}}\:\Rightarrow \\ $$$${J}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−{y}} \:−{e}^{−\mathrm{2}{y}} }{{y}}{dy}\:\:{let}\:{f}\left({u}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−{y}} −{e}^{−\mathrm{2}{y}} }{{y}}\:{e}^{−{yu}} \:{dy}\:{with}\:{u}\geqslant\mathrm{0} \\ $$$${we}\:{have}\:{f}^{'} \left({u}\right)\:=−\int_{\mathrm{0}} ^{\infty} \:\:\left({e}^{−{y}} −{e}^{−\mathrm{2}{y}} \right){e}^{−{yu}} \:{dy} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \left({e}^{−\left({u}+\mathrm{2}\right){y}} −{e}^{−\left({u}+\mathrm{1}\right){y}} \right){dy}\:=\left[\frac{−\mathrm{1}}{{u}+\mathrm{2}}{e}^{−\left({u}+\mathrm{2}\right){y}} +\frac{\mathrm{1}}{{u}+\mathrm{1}}{e}^{−\left({u}+\mathrm{1}\right){y}} \right]_{\mathrm{0}} ^{\infty} \\ $$$$=\frac{\mathrm{1}}{{u}+\mathrm{2}}−\frac{\mathrm{1}}{{u}+\mathrm{1}}\:\Rightarrow{f}\left({u}\right)\:={ln}\mid\frac{{u}+\mathrm{2}}{{u}+\mathrm{1}}\mid\:+{c} \\ $$$${due}\:{to}\:{the}\:{continuity}\:\:\exists{m}>\mathrm{0}\:/\mid{f}\left({u}\right)\mid\leqslant{m}\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{yu}} {dy}\:=\frac{{m}}{{u}}\:\rightarrow\mathrm{0}\left({u}\rightarrow+\infty\right) \\ $$$$\Rightarrow{c}=\mathrm{0}\:\Rightarrow{f}\left({u}\right)={ln}\mid\frac{{u}+\mathrm{2}}{{u}+\mathrm{1}}\mid \\ $$$${J}={f}\left(\mathrm{0}\right)\:={ln}\mid\frac{\mathrm{2}}{\mathrm{1}}\mid\:={ln}\left(\mathrm{2}\right) \\ $$$$ \\ $$$$ \\ $$
Answered by mind is power last updated on 15/Nov/19
![j=∫_0 ^(+∞) [(e^(−2xy) /(−y))+(e^(−xy) /y)]_0 ^1 dy =∫_0 ^(+∞) {(e^(−2y) /(−y))+(e^(−y) /y)+(1/y)−(1/y)}dy =∫_0 ^(+∞) ((e^(−y) −e^(−2y) )/y)dy ∫_0 ^(+∞) ((f(ax)−f(bx))/x)dx=−f(0)ln((a/b)) if f continus withe limx→∞ f(x)=0 ∫_0 ^(+∞) ∫_b ^a f′(tx)dt.dx=∫_0 ^(+∞) [((f(tx))/x)]_b ^a dx=∫_0 ^(+∞) ((f(ax)−f(bx))/x).dx we use fubini ∫∫f(x,y)dxdy=∫∫f(x,y)dydx⇒ ∫((f(ax)−f(bx))/x)dx=∫_b ^a ∫_0 ^(+∞) f′(tx)dxdt=∫_b ^a [((f(tx))/t)]_0 ^(+∞) dt=∫_b ^a ((−f(0))/t)dt=−f(0)ln(∣(a/b)∣) in our exemple a=−1,b=−2 f(y)=e^(−y) ,f(0)=1,lim_(y→∞) f(y)=0 ⇒∫_0 ^(+∞) ((e^(−y) −e^(−2y) )/y)dy=−1ln(∣((−1)/(−2))∣)=ln(2)](Q73752.png)
$${j}=\int_{\mathrm{0}} ^{+\infty} \left[\frac{{e}^{−\mathrm{2}{xy}} }{−{y}}+\frac{{e}^{−{xy}} }{{y}}\right]_{\mathrm{0}} ^{\mathrm{1}} {dy} \\ $$$$=\int_{\mathrm{0}} ^{+\infty} \left\{\frac{{e}^{−\mathrm{2}{y}} }{−{y}}+\frac{{e}^{−{y}} }{{y}}+\frac{\mathrm{1}}{{y}}−\frac{\mathrm{1}}{{y}}\right\}{dy} \\ $$$$=\int_{\mathrm{0}} ^{+\infty} \frac{{e}^{−{y}} −{e}^{−\mathrm{2}{y}} }{{y}}{dy} \\ $$$$\int_{\mathrm{0}} ^{+\infty} \frac{{f}\left({ax}\right)−{f}\left({bx}\right)}{{x}}{dx}=−{f}\left(\mathrm{0}\right){ln}\left(\frac{{a}}{{b}}\right) \\ $$$${if}\:{f}\:{continus}\:\:{withe}\:{limx}\rightarrow\infty\:{f}\left({x}\right)=\mathrm{0} \\ $$$$\int_{\mathrm{0}} ^{+\infty} \int_{{b}} ^{{a}} {f}'\left({tx}\right){dt}.{dx}=\int_{\mathrm{0}} ^{+\infty} \left[\frac{{f}\left({tx}\right)}{{x}}\right]_{{b}} ^{{a}} {dx}=\int_{\mathrm{0}} ^{+\infty} \frac{{f}\left({ax}\right)−{f}\left({bx}\right)}{{x}}.{dx} \\ $$$${we}\:{use}\:{fubini}\:\int\int{f}\left({x},{y}\right){dxdy}=\int\int{f}\left({x},{y}\right){dydx}\Rightarrow \\ $$$$\int\frac{{f}\left({ax}\right)−{f}\left({bx}\right)}{{x}}{dx}=\int_{{b}} ^{{a}} \int_{\mathrm{0}} ^{+\infty} {f}'\left({tx}\right){dxdt}=\int_{{b}} ^{{a}} \left[\frac{{f}\left({tx}\right)}{{t}}\right]_{\mathrm{0}} ^{+\infty} {dt}=\int_{{b}} ^{{a}} \frac{−{f}\left(\mathrm{0}\right)}{{t}}{dt}=−{f}\left(\mathrm{0}\right){ln}\left(\mid\frac{{a}}{{b}}\mid\right) \\ $$$${in}\:{our}\:{exemple}\:{a}=−\mathrm{1},{b}=−\mathrm{2} \\ $$$${f}\left({y}\right)={e}^{−{y}} ,{f}\left(\mathrm{0}\right)=\mathrm{1},\underset{{y}\rightarrow\infty} {\mathrm{lim}}\:{f}\left({y}\right)=\mathrm{0}\:\:\: \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{+\infty} \frac{{e}^{−{y}} −{e}^{−\mathrm{2}{y}} }{{y}}{dy}=−\mathrm{1}{ln}\left(\mid\frac{−\mathrm{1}}{−\mathrm{2}}\mid\right)={ln}\left(\mathrm{2}\right) \\ $$
Commented by ~blr237~ last updated on 15/Nov/19
$${Thanks}\:{sir} \\ $$
Commented by mind is power last updated on 15/Nov/19
$${y}'{re}\:{welcom} \\ $$