
Question and Answers Forum
Question Number 73832 by FCB last updated on 16/Nov/19

Commented by FCB last updated on 16/Nov/19

Commented by MJS last updated on 16/Nov/19
Commented by peter frank last updated on 16/Nov/19
Commented by MJS last updated on 16/Nov/19
Commented by peter frank last updated on 16/Nov/19
Commented by FCB last updated on 16/Nov/19

Commented by MJS last updated on 16/Nov/19
Answered by peter frank last updated on 16/Nov/19
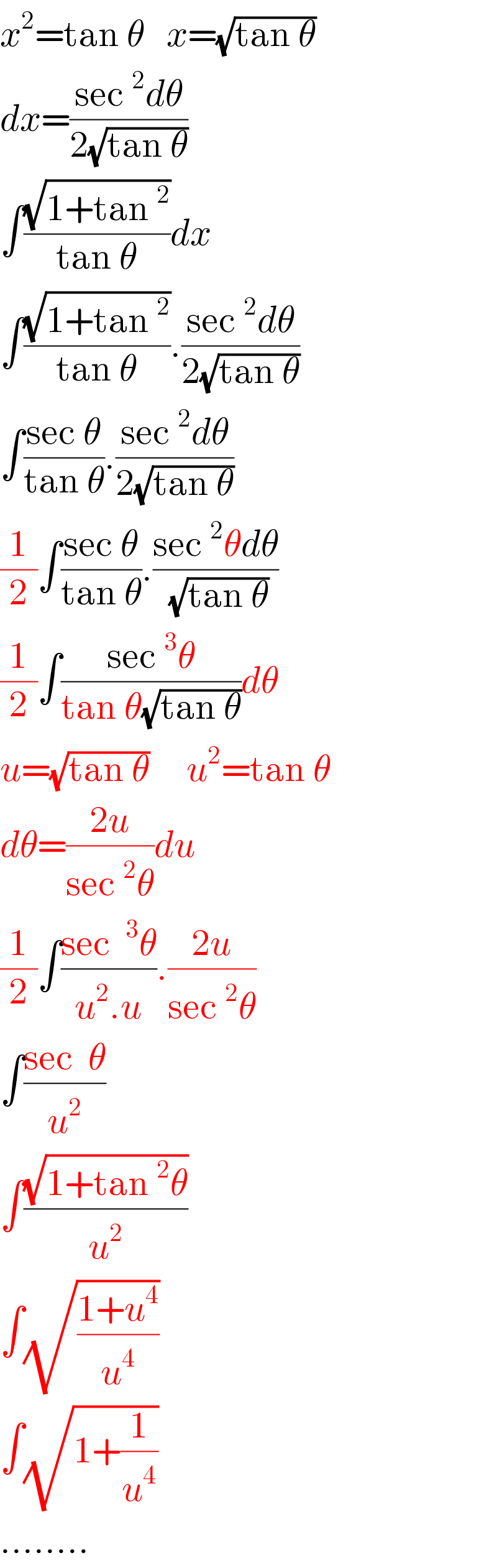
Commented by FCB last updated on 16/Nov/19

Commented by FCB last updated on 16/Nov/19

Commented by FCB last updated on 16/Nov/19

Commented by FCB last updated on 16/Nov/19

Commented by peter frank last updated on 16/Nov/19
Commented by mind is power last updated on 16/Nov/19
![∫((√(1+x^4 ))/x^2 )dx=((−(√(1+x^4 )))/x)+∫((2x^3 )/(x(√(1+x^4 ))))dx we devloppe ∫((2x^2 )/(√(1+x^4 )))dx x=e^(i(π/4)) .sh(t)⇒dx=e^(i(π/4)) ch(t) ⇒∫_0 ^x ((2x^2 dx)/(√(1+x^4 )))=2e^(i(π/4)) ∫_0 ^(sh^− (xe^(−((iπ)/4)) )) .((ish^2 (t)ch(t))/(√(1−sh^4 (t)))) =2ie^(i(π/4)) ∫_0 ^(sh^− (xe^(−((iπ)/4)) )) ((sh^2 (t)ch(t))/(√((1−sh^2 (t))(1+sh^2 (t)))))dt =2ie^(i(π/4)) ∫_0 ^(sh^− (xe^(−((iπ)/4)) )) ((sh^2 (t)ch(t))/((√(1−sh^2 (t))).ch(t)))dt 2ie^(i(π/4)) ∫_0 ^(sh^− (xe^(−((iπ)/4)) )) ((sh^2 (t))/((√(1−sh^2 (t))).))dt t=is sh(is)=isin(s) ⇔−2e^(i(π/4)) ∫_0 ^(−ish^− (xe^(−((iπ)/4)) )) ((sin^2 (t))/(√(1+sin^2 (t)))) ⇔−2e^(i(π/4)) ∫_0 ^(−ish^− (xe^(−((iπ)/4)) )) ((sin^2 (t)+1−1)/(√(1+sin^2 (t)))) ⇔−2e^(i(π/4)) ∫_0 ^(−ish^− (xe^(−((iπ)/4)) )) (√(1−(i)^2 sin^2 (t)))−2(−e^(i(π/4)) )∫_0 ^(−ish^− (xe^(−((iπ)/4)) )) (dt/(√(1−(i)^2 sin^2 (t)))) E(θ⌋k^2 )=∫_0 ^θ (dϕ/(√(1−k^2 sin^2 (ϕ)))),2nd eleptic function F(θ]k^2 )=∫_0 ^θ (√(1−(k^2 )sin^2 (ϕ)))dϕ so we get −2e^(i(π/4)) F(−ish^− (xe^(i(π/4)) )∣−1)−(−2e^(i(π/4)) )E(−ish(xe^(i(π/4)) )∣−1) to finish e^(i(π/4)) =(−1)^(1/4) ∫((√(1+x^4 ))/x^2 )dx=((−(√(1+x^4 )))/x)+∫((2x^3 )/(x(√(1+x^4 ))))dx −((√(1+x^4 ))/x)=−(1/(x(√(1+x^4 ))))−(x^3 /(√(1+x^4 ))) we get the answer](Q73947.png)
Commented by MJS last updated on 17/Nov/19

Commented by mind is power last updated on 17/Nov/19

Commented by FCB last updated on 17/Nov/19

Answered by Tanmay chaudhury last updated on 17/Nov/19

