Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 73838 by liki last updated on 16/Nov/19

Commented by liki last updated on 16/Nov/19

.. I need help plz ;Qn 4(a) ii, (d) i and ii

$$..\:{I}\:{need}\:{help}\:{plz}\:;{Qn}\:\mathrm{4}\left({a}\right)\:{ii},\:\left({d}\right)\:{i}\:{and}\:{ii}\: \\ $$

Commented by mathmax by abdo last updated on 16/Nov/19

4 ii) let S=2×3 +3×4 +4×5+...(nterms) ⇒ S=Σ_(k=2) ^(n+1) k(k+1) =Σ_(k=2) ^(n+1) k^2 +Σ_(k=2) ^(n+1) k =Σ_(k=1) ^(n+1) k^2 +Σ_(k=1) ^(n+1) k −2 =(((n+1)(n+2)(2(n+1)+1))/6) +(((n+1)(n+2)/2)−2 =(((n+1)(n+2)(2n+3))/6) +((3(n+1)(n+2))/6) =(((n+1)(n+2))/6){ 2n+3 +3} =(((n+1)(n+2)(2n+6))/6) S=(((n+1)(n+2)(n+3))/3) .

$$\left.\mathrm{4}\:{ii}\right)\:\:{let}\:{S}=\mathrm{2}×\mathrm{3}\:+\mathrm{3}×\mathrm{4}\:+\mathrm{4}×\mathrm{5}+...\left({nterms}\right)\:\Rightarrow \\ $$$${S}=\sum_{{k}=\mathrm{2}} ^{{n}+\mathrm{1}} {k}\left({k}+\mathrm{1}\right)\:=\sum_{{k}=\mathrm{2}} ^{{n}+\mathrm{1}} {k}^{\mathrm{2}} \:+\sum_{{k}=\mathrm{2}} ^{{n}+\mathrm{1}} {k} \\ $$$$=\sum_{{k}=\mathrm{1}} ^{{n}+\mathrm{1}} {k}^{\mathrm{2}} \:+\sum_{{k}=\mathrm{1}} ^{{n}+\mathrm{1}} {k}\:−\mathrm{2}\:=\frac{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\left(\mathrm{2}\left({n}+\mathrm{1}\right)+\mathrm{1}\right)}{\mathrm{6}}\:+\frac{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right.}{\mathrm{2}}−\mathrm{2} \\ $$$$=\frac{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\left(\mathrm{2}{n}+\mathrm{3}\right)}{\mathrm{6}}\:+\frac{\mathrm{3}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}{\mathrm{6}} \\ $$$$=\frac{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}{\mathrm{6}}\left\{\:\mathrm{2}{n}+\mathrm{3}\:+\mathrm{3}\right\}\:=\frac{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\left(\mathrm{2}{n}+\mathrm{6}\right)}{\mathrm{6}} \\ $$$${S}=\frac{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)}{\mathrm{3}}\:. \\ $$

Commented by mathmax by abdo last updated on 16/Nov/19

forgive S=(((n+1)(n+2)(n+3))/3) −2.

$${forgive}\:{S}=\frac{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)}{\mathrm{3}}\:−\mathrm{2}. \\ $$

Commented by mathmax by abdo last updated on 16/Nov/19

4)b) F(x)=((2x^2 +8x +7)/((x+2)(x+3))) =((2x^2 +8x +7)/(x^2 +5x +6)) =((2(x^2 +5x +6)−10x −12+8x+7)/(x^2 +5x +6))=2 −((2x+5)/(x^2 +5x +6)) let f(x)=((2x+5)/(x^2 +5x +6)) =((2x+5)/((x+2)(x+3))) =(a/(x+2)) +(b/(x+3)) a=(x+2)f(x)∣_(x=−2) =(1/1) =1 b=(x+3)f(x)∣_(x=−3) =((−1)/(−1)) =1 ⇒ F(x)=2−(1/(x+2))−(1/(x+3))

$$\left.\mathrm{4}\left.\right){b}\right)\:\:{F}\left({x}\right)=\frac{\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{8}{x}\:+\mathrm{7}}{\left({x}+\mathrm{2}\right)\left({x}+\mathrm{3}\right)}\:=\frac{\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{8}{x}\:+\mathrm{7}}{{x}^{\mathrm{2}} +\mathrm{5}{x}\:+\mathrm{6}} \\ $$$$=\frac{\mathrm{2}\left({x}^{\mathrm{2}} \:+\mathrm{5}{x}\:+\mathrm{6}\right)−\mathrm{10}{x}\:−\mathrm{12}+\mathrm{8}{x}+\mathrm{7}}{{x}^{\mathrm{2}} +\mathrm{5}{x}\:+\mathrm{6}}=\mathrm{2}\:−\frac{\mathrm{2}{x}+\mathrm{5}}{{x}^{\mathrm{2}} \:+\mathrm{5}{x}\:+\mathrm{6}}\:{let} \\ $$$${f}\left({x}\right)=\frac{\mathrm{2}{x}+\mathrm{5}}{{x}^{\mathrm{2}} \:+\mathrm{5}{x}\:+\mathrm{6}}\:=\frac{\mathrm{2}{x}+\mathrm{5}}{\left({x}+\mathrm{2}\right)\left({x}+\mathrm{3}\right)}\:=\frac{{a}}{{x}+\mathrm{2}}\:+\frac{{b}}{{x}+\mathrm{3}} \\ $$$${a}=\left({x}+\mathrm{2}\right){f}\left({x}\right)\mid_{{x}=−\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{1}}\:=\mathrm{1} \\ $$$${b}=\left({x}+\mathrm{3}\right){f}\left({x}\right)\mid_{{x}=−\mathrm{3}} \:\:=\frac{−\mathrm{1}}{−\mathrm{1}}\:=\mathrm{1}\:\Rightarrow \\ $$$${F}\left({x}\right)=\mathrm{2}−\frac{\mathrm{1}}{{x}+\mathrm{2}}−\frac{\mathrm{1}}{{x}+\mathrm{3}} \\ $$

Commented by mathmax by abdo last updated on 16/Nov/19

4di) we have (3x−(2/x^2 ))^(18) =(((3x^3 −2)^(18) )/x^(36) ) =(1/x^(36) )Σ_(k=0) ^(18) C_(18) ^k (3x^3 )^k (−2)^(18−k) =(1/x^(36) )Σ_(k=0) ^(18) C_(18) ^k 3^k x^(3k) (−2)^(18−k) =Σ_(k=0) ^(18) (−2)^(18−k) 3^k C_(18) ^k x^(3k−36) we get the independent term if 3k−36=0 ⇒k=12 ⇒ a_0 =(−2)^(18−12) 3^(12) C_(18) ^(12) =(−2)^6 ×3^(12) × C_(18) ^(12)

$$\left.\mathrm{4}{di}\right)\:\:{we}\:{have}\:\left(\mathrm{3}{x}−\frac{\mathrm{2}}{{x}^{\mathrm{2}} }\right)^{\mathrm{18}} \:=\frac{\left(\mathrm{3}{x}^{\mathrm{3}} −\mathrm{2}\right)^{\mathrm{18}} }{{x}^{\mathrm{36}} } \\ $$$$=\frac{\mathrm{1}}{{x}^{\mathrm{36}} }\sum_{{k}=\mathrm{0}} ^{\mathrm{18}} \:{C}_{\mathrm{18}} ^{{k}} \left(\mathrm{3}{x}^{\mathrm{3}} \right)^{{k}} \left(−\mathrm{2}\right)^{\mathrm{18}−{k}} \:\:=\frac{\mathrm{1}}{{x}^{\mathrm{36}} }\sum_{{k}=\mathrm{0}} ^{\mathrm{18}} \:{C}_{\mathrm{18}} ^{{k}} \:\mathrm{3}^{{k}} \:{x}^{\mathrm{3}{k}} \left(−\mathrm{2}\right)^{\mathrm{18}−{k}} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{\mathrm{18}} \:\left(−\mathrm{2}\right)^{\mathrm{18}−{k}} \:\mathrm{3}^{{k}} \:{C}_{\mathrm{18}} ^{{k}} \:{x}^{\mathrm{3}{k}−\mathrm{36}} \:\:\:\:{we}\:{get}\:{the}\:{independent}\:{term}\:{if} \\ $$$$\mathrm{3}{k}−\mathrm{36}=\mathrm{0}\:\Rightarrow{k}=\mathrm{12}\:\Rightarrow\:{a}_{\mathrm{0}} =\left(−\mathrm{2}\right)^{\mathrm{18}−\mathrm{12}} \:\mathrm{3}^{\mathrm{12}} \:{C}_{\mathrm{18}} ^{\mathrm{12}} \\ $$$$=\left(−\mathrm{2}\right)^{\mathrm{6}} \:×\mathrm{3}^{\mathrm{12}} ×\:{C}_{\mathrm{18}} ^{\mathrm{12}} \\ $$

Commented by liki last updated on 16/Nov/19

...Thanks sir

$$...{Thanks}\:{sir} \\ $$

Commented by abdomathmax last updated on 16/Nov/19

you are welcome.

$${you}\:{are}\:{welcome}. \\ $$

Commented by mathmax by abdo last updated on 16/Nov/19

M = (((1 0 0)),((x 2 0)) ) (3 1 1) the caracteristic polynom of M is det (M−αI) = determinant (((1−α 0 0)),((x 2−α 0))) ∣3 1 1−α∣ =(1−α) determinant (((2−α 0)),((1 1−α)))−x determinant (((0 0)),((1 1−α)))+3 determinant (((0 0)),((2−α 0))) =(1−α)(2−α)(1−α) =(α−1)^2 (2−α) =(α^2 −2α +1)(2−α) =2α^2 −4α +2−α^3 +2α^2 −α =−α^3 +4α^2 −5α +2 Cayler hamilton theorem give −M^3 +4M^2 −5M +2I =0 ⇒ 2I =M^3 −4M^2 +5M ⇒(1/2)M(M^2 −4M +5I) =I ⇒ M^(−1) =(1/2)(M^2 −4M +5I) rest to finish the calculus....

$${M}\:=\:\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{0}}\\{{x}\:\:\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\mathrm{0}}\end{pmatrix} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{3}\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\mathrm{1}\right) \\ $$$${the}\:{caracteristic}\:{polynom}\:{of}\:{M}\:{is} \\ $$$${det}\:\left({M}−\alpha{I}\right)\:=\begin{vmatrix}{\mathrm{1}−\alpha\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{{x}\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}−\alpha\:\:\:\:\:\:\:\:\mathrm{0}}\end{vmatrix} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\mathrm{1}−\alpha\mid \\ $$$$=\left(\mathrm{1}−\alpha\right)\begin{vmatrix}{\mathrm{2}−\alpha\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}−\alpha}\end{vmatrix}−{x}\begin{vmatrix}{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{1}\:\:\:\:\:\:\:\:\:\mathrm{1}−\alpha}\end{vmatrix}+\mathrm{3}\:\begin{vmatrix}{\mathrm{0}\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{2}−\alpha\:\mathrm{0}}\end{vmatrix} \\ $$$$=\left(\mathrm{1}−\alpha\right)\left(\mathrm{2}−\alpha\right)\left(\mathrm{1}−\alpha\right) \\ $$$$=\left(\alpha−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{2}−\alpha\right)\:=\left(\alpha^{\mathrm{2}} −\mathrm{2}\alpha\:+\mathrm{1}\right)\left(\mathrm{2}−\alpha\right) \\ $$$$=\mathrm{2}\alpha^{\mathrm{2}} −\mathrm{4}\alpha\:+\mathrm{2}−\alpha^{\mathrm{3}} +\mathrm{2}\alpha^{\mathrm{2}} \:−\alpha\:=−\alpha^{\mathrm{3}} +\mathrm{4}\alpha^{\mathrm{2}} \:−\mathrm{5}\alpha\:+\mathrm{2} \\ $$$${Cayler}\:{hamilton}\:{theorem}\:\:\:{give} \\ $$$$−{M}^{\mathrm{3}} \:+\mathrm{4}{M}^{\mathrm{2}} −\mathrm{5}{M}\:+\mathrm{2}{I}\:=\mathrm{0}\:\:\Rightarrow \\ $$$$\mathrm{2}{I}\:={M}^{\mathrm{3}} −\mathrm{4}{M}^{\mathrm{2}} +\mathrm{5}{M}\:\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}{M}\left({M}^{\mathrm{2}} −\mathrm{4}{M}\:+\mathrm{5}{I}\right)\:={I}\:\Rightarrow \\ $$$${M}^{−\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\left({M}^{\mathrm{2}} −\mathrm{4}{M}\:+\mathrm{5}{I}\right)\:\:{rest}\:{to}\:{finish}\:{the}\:{calculus}.... \\ $$

Commented by mathmax by abdo last updated on 16/Nov/19

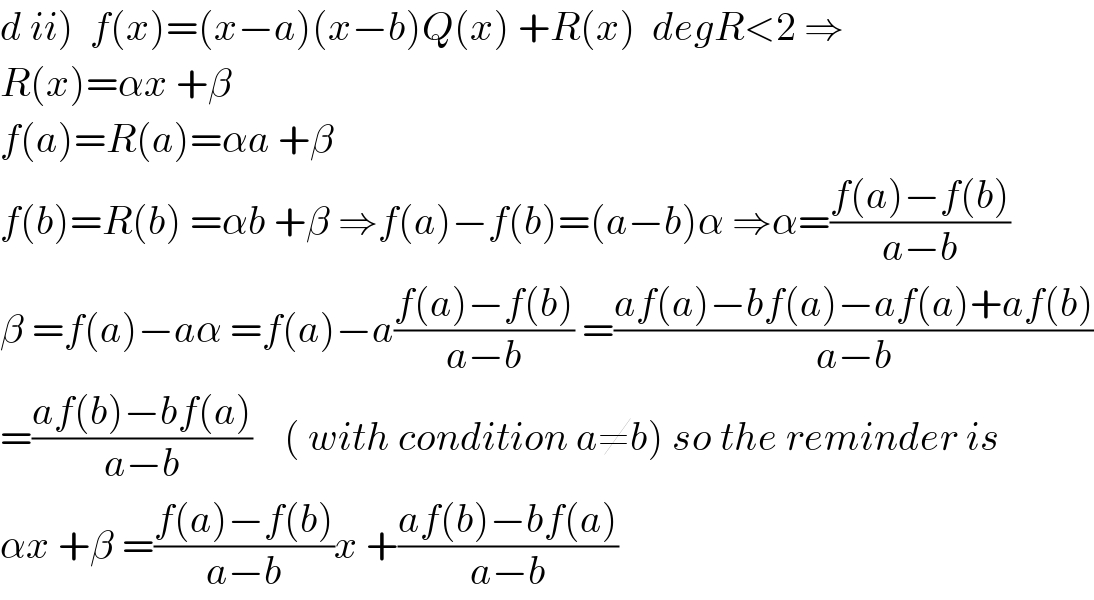
d ii) f(x)=(x−a)(x−b)Q(x) +R(x) degR<2 ⇒ R(x)=αx +β f(a)=R(a)=αa +β f(b)=R(b) =αb +β ⇒f(a)−f(b)=(a−b)α ⇒α=((f(a)−f(b))/(a−b)) β =f(a)−aα =f(a)−a((f(a)−f(b))/(a−b)) =((af(a)−bf(a)−af(a)+af(b))/(a−b)) =((af(b)−bf(a))/(a−b)) ( with condition a≠b) so the reminder is αx +β =((f(a)−f(b))/(a−b))x +((af(b)−bf(a))/(a−b))

$$\left.{d}\:{ii}\right)\:\:{f}\left({x}\right)=\left({x}−{a}\right)\left({x}−{b}\right){Q}\left({x}\right)\:+{R}\left({x}\right)\:\:{degR}<\mathrm{2}\:\Rightarrow \\ $$$${R}\left({x}\right)=\alpha{x}\:+\beta \\ $$$${f}\left({a}\right)={R}\left({a}\right)=\alpha{a}\:+\beta \\ $$$${f}\left({b}\right)={R}\left({b}\right)\:=\alpha{b}\:+\beta\:\Rightarrow{f}\left({a}\right)−{f}\left({b}\right)=\left({a}−{b}\right)\alpha\:\Rightarrow\alpha=\frac{{f}\left({a}\right)−{f}\left({b}\right)}{{a}−{b}} \\ $$$$\beta\:={f}\left({a}\right)−{a}\alpha\:={f}\left({a}\right)−{a}\frac{{f}\left({a}\right)−{f}\left({b}\right)}{{a}−{b}}\:=\frac{{af}\left({a}\right)−{bf}\left({a}\right)−{af}\left({a}\right)+{af}\left({b}\right)}{{a}−{b}} \\ $$$$=\frac{{af}\left({b}\right)−{bf}\left({a}\right)}{{a}−{b}}\:\:\:\:\left(\:{with}\:{condition}\:{a}\neq{b}\right)\:{so}\:{the}\:{reminder}\:{is} \\ $$$$\alpha{x}\:+\beta\:=\frac{{f}\left({a}\right)−{f}\left({b}\right)}{{a}−{b}}{x}\:+\frac{{af}\left({b}\right)−{bf}\left({a}\right)}{{a}−{b}} \\ $$

Answered by Tanmay chaudhury last updated on 16/Nov/19

S=2×3+3×4×4×5+... T_n =[2+(n−1)×1]×[3+(n−1)×1] =(n+1)(n+2)=n^2 +3n+2 S_n =ΣT_n =Σ_(n=1) ^n n^2 +3Σ_(n=1) ^n n+2Σ_(n=1) ^n 1 S_n =((n(n+1)(2n+1))/6)+3×((n(n+1))/2)+2n

$${S}=\mathrm{2}×\mathrm{3}+\mathrm{3}×\mathrm{4}×\mathrm{4}×\mathrm{5}+... \\ $$$${T}_{{n}} =\left[\mathrm{2}+\left({n}−\mathrm{1}\right)×\mathrm{1}\right]×\left[\mathrm{3}+\left({n}−\mathrm{1}\right)×\mathrm{1}\right] \\ $$$$=\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)={n}^{\mathrm{2}} +\mathrm{3}{n}+\mathrm{2} \\ $$$${S}_{{n}} =\Sigma{T}_{{n}} =\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}{n}^{\mathrm{2}} +\mathrm{3}\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}{n}+\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{1} \\ $$$${S}_{{n}} =\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}+\mathrm{3}×\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}+\mathrm{2}{n} \\ $$

Answered by Tanmay chaudhury last updated on 16/Nov/19

d(i) let (r+1)th term is indepdndent of x (x^0 ) 18_C_r (3x)^(18−r) ×(((−2)/x^2 ))^r 18_(C_r ) ×3^(18−r) ×x^(18−r) ×(−1)^r ×2^r ×(1/x^(2r) ) 18_C_r ×3^(18−r) ×x^(18−3r) ×(−1)^r ×2^r so x^(18−3r) =x^0 →3r=18 r=6 18_C_6 ×3^(18−6) ×(−1)^6 ×2^6 ((18!)/(6!12!))×3^(12) ×2^6

$${d}\left({i}\right)\:\:{let}\:\left({r}+\mathrm{1}\right){th}\:{term}\:{is}\:{indepdndent}\:{of}\:{x}\:\left({x}^{\mathrm{0}} \right) \\ $$$$\mathrm{18}_{{C}_{{r}} } \left(\mathrm{3}{x}\right)^{\mathrm{18}−{r}} ×\left(\frac{−\mathrm{2}}{{x}^{\mathrm{2}} }\right)^{{r}} \\ $$$$\mathrm{18}_{{C}_{{r}} \:} ×\mathrm{3}^{\mathrm{18}−{r}} ×{x}^{\mathrm{18}−{r}} ×\left(−\mathrm{1}\right)^{{r}} ×\mathrm{2}^{{r}} ×\frac{\mathrm{1}}{{x}^{\mathrm{2}{r}} } \\ $$$$\mathrm{18}_{{C}_{{r}} } ×\mathrm{3}^{\mathrm{18}−{r}} ×{x}^{\mathrm{18}−\mathrm{3}{r}} ×\left(−\mathrm{1}\right)^{{r}} ×\mathrm{2}^{{r}} \\ $$$${so}\:\:{x}^{\mathrm{18}−\mathrm{3}{r}} ={x}^{\mathrm{0}} \:\:\:\rightarrow\mathrm{3}{r}=\mathrm{18}\:\:\:\:{r}=\mathrm{6} \\ $$$$\mathrm{18}_{{C}_{\mathrm{6}} } ×\mathrm{3}^{\mathrm{18}−\mathrm{6}} ×\left(−\mathrm{1}\right)^{\mathrm{6}} ×\mathrm{2}^{\mathrm{6}} \\ $$$$\frac{\mathrm{18}!}{\mathrm{6}!\mathrm{12}!}×\mathrm{3}^{\mathrm{12}} ×\mathrm{2}^{\mathrm{6}} \\ $$

Commented by liki last updated on 16/Nov/19

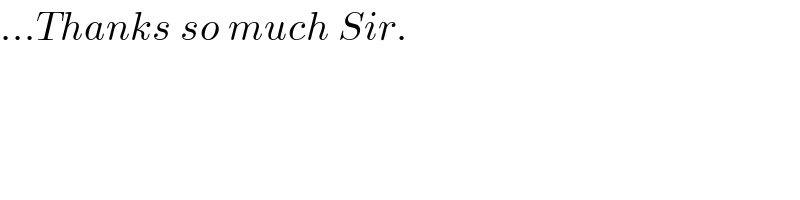
...Thanks so much Sir.

$$...{Thanks}\:{so}\:{much}\:{Sir}. \\ $$

Commented by Tanmay chaudhury last updated on 16/Nov/19

most welcome...

$${most}\:{welcome}... \\ $$

Answered by Tanmay chaudhury last updated on 16/Nov/19

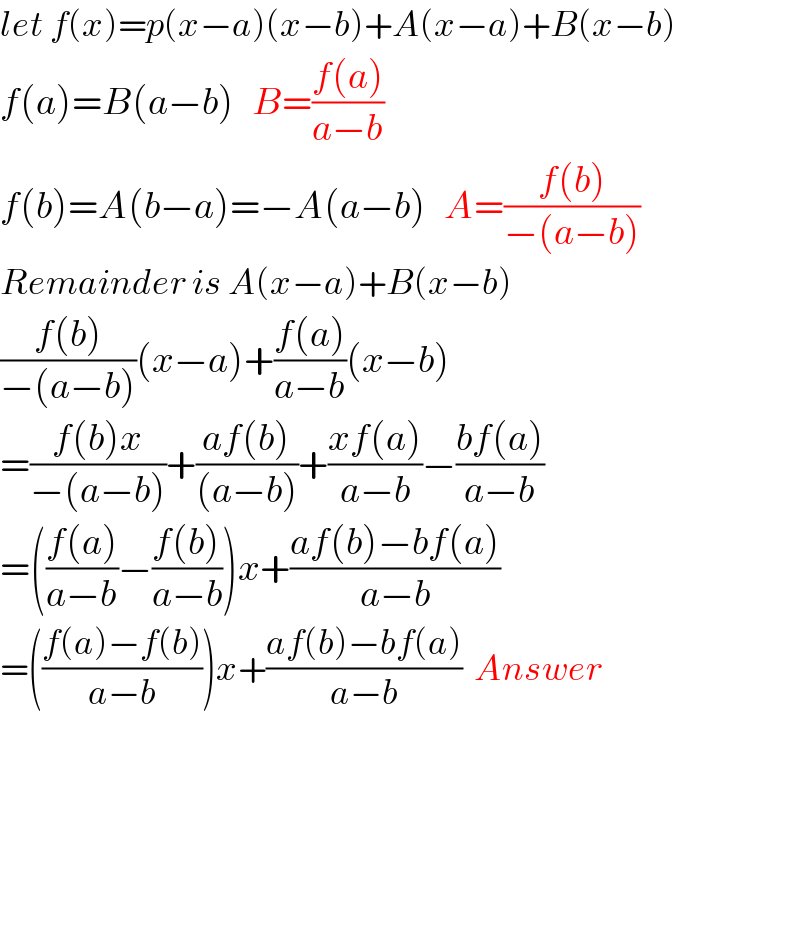
let f(x)=p(x−a)(x−b)+A(x−a)+B(x−b) f(a)=B(a−b) B=((f(a))/(a−b)) f(b)=A(b−a)=−A(a−b) A=((f(b))/(−(a−b))) Remainder is A(x−a)+B(x−b) ((f(b))/(−(a−b)))(x−a)+((f(a))/(a−b))(x−b) =((f(b)x)/(−(a−b)))+((af(b))/((a−b)))+((xf(a))/(a−b))−((bf(a))/(a−b)) =(((f(a))/(a−b))−((f(b))/(a−b)))x+((af(b)−bf(a))/(a−b)) =(((f(a)−f(b))/(a−b)))x+((af(b)−bf(a))/(a−b)) Answer

$${let}\:{f}\left({x}\right)={p}\left({x}−{a}\right)\left({x}−{b}\right)+{A}\left({x}−{a}\right)+{B}\left({x}−{b}\right) \\ $$$${f}\left({a}\right)={B}\left({a}−{b}\right)\:\:\:{B}=\frac{{f}\left({a}\right)}{{a}−{b}} \\ $$$${f}\left({b}\right)={A}\left({b}−{a}\right)=−{A}\left({a}−{b}\right)\:\:\:{A}=\frac{{f}\left({b}\right)}{−\left({a}−{b}\right)} \\ $$$${Remainder}\:{is}\:{A}\left({x}−{a}\right)+{B}\left({x}−{b}\right) \\ $$$$\frac{{f}\left({b}\right)}{−\left({a}−{b}\right)}\left({x}−{a}\right)+\frac{{f}\left({a}\right)}{{a}−{b}}\left({x}−{b}\right) \\ $$$$=\frac{{f}\left({b}\right){x}}{−\left({a}−{b}\right)}+\frac{{af}\left({b}\right)}{\left({a}−{b}\right)}+\frac{{xf}\left({a}\right)}{{a}−{b}}−\frac{{bf}\left({a}\right)}{{a}−{b}} \\ $$$$=\left(\frac{{f}\left({a}\right)}{{a}−{b}}−\frac{{f}\left({b}\right)}{{a}−{b}}\right){x}+\frac{{af}\left({b}\right)−{bf}\left({a}\right)}{{a}−{b}} \\ $$$$=\left(\frac{{f}\left({a}\right)−{f}\left({b}\right)}{{a}−{b}}\right){x}+\frac{{af}\left({b}\right)−{bf}\left({a}\right)}{{a}−{b}}\:\:{Answer} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by liki last updated on 16/Nov/19

God bless you sir.

$${God}\:{bless}\:{you}\:{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com