
Question Number 7399 by Tawakalitu. last updated on 27/Aug/16
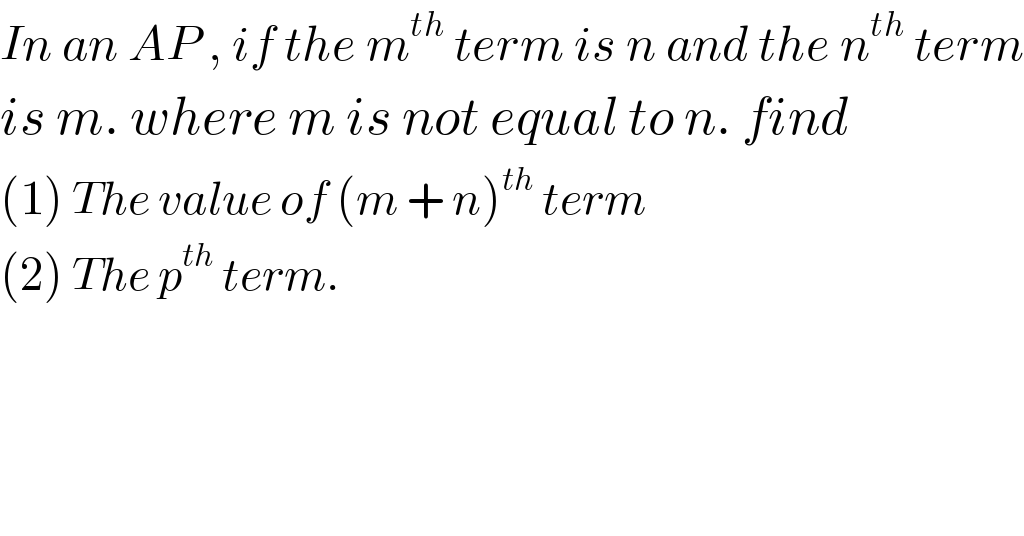
$${In}\:{an}\:{AP}\:,\:{if}\:{the}\:{m}^{{th}} \:{term}\:{is}\:{n}\:{and}\:{the}\:{n}^{{th}} \:{term} \\ $$$${is}\:{m}.\:{where}\:{m}\:{is}\:{not}\:{equal}\:{to}\:{n}.\:{find} \\ $$$$\left(\mathrm{1}\right)\:{The}\:{value}\:{of}\:\left({m}\:+\:{n}\right)^{{th}} \:{term} \\ $$$$\left(\mathrm{2}\right)\:{The}\:{p}^{{th}} \:{term}. \\ $$
Answered by Yozzia last updated on 27/Aug/16

$${For}\:{an}\:{AP},\:{the}\:{k}^{{th}} \:{term}\:{u}\left({k}\right)\:{is}\:{given}\:{by} \\ $$$${u}\left({k}\right)={u}\left(\mathrm{1}\right)+\left({k}−\mathrm{1}\right){d}\:{where}\:{d}\:{is}\:{a}\:{constant}. \\ $$$$\therefore\:{k}={m}\Rightarrow{u}\left({m}\right)={u}\left(\mathrm{1}\right)+\left({m}−\mathrm{1}\right){d}={n} \\ $$$${and}\:{k}={n}\Rightarrow{u}\left({n}\right)={u}\left(\mathrm{1}\right)+\left({n}−\mathrm{1}\right){d}={m} \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:{k}={m}+{n}\Rightarrow{u}\left({m}+{n}\right)={u}\left(\mathrm{1}\right)+\left({m}+{n}−\mathrm{1}\right){d} \\ $$$${But},\:{n}−{m}=\left({m}−{n}\right){d}\:\:{and}\:{m}\neq{n}\Rightarrow{d}=−\mathrm{1} \\ $$$$\therefore{u}\left({m}+{n}\right)={u}\left(\mathrm{1}\right)+\left({m}+{n}−\mathrm{1}\right)\left(−\mathrm{1}\right) \\ $$$${but},\:{n}+{m}=\mathrm{2}{u}\left(\mathrm{1}\right)+\left(−\mathrm{1}\right)\left({m}+{n}−\mathrm{2}\right) \\ $$$$\mathrm{2}\left({m}+{n}\right)=\mathrm{2}{u}\left(\mathrm{1}\right)+\mathrm{2} \\ $$$${u}\left(\mathrm{1}\right)={m}+{n}−\mathrm{1} \\ $$$$\therefore\:{u}\left({m}+{n}\right)={m}+{n}−\mathrm{1}+\left(−\mathrm{1}\right)\left({m}+{n}−\mathrm{1}\right)=\mathrm{0} \\ $$$$ \\ $$$$\left(\mathrm{2}\right)\:{k}={p}\Rightarrow\:{u}\left({p}\right)={m}+{n}−\mathrm{1}+\left({p}−\mathrm{1}\right)\left(−\mathrm{1}\right)={m}+{n}−{p} \\ $$
Commented by Rasheed Soomro last updated on 27/Aug/16

$${Another}\:{way} \\ $$$${From}\:{the}\:{above}\:\:{d}=−\mathrm{1} \\ $$$${u}\left(\mathrm{1}\right)+\left({m}−\mathrm{1}\right){d}={n} \\ $$$${adding}\:{nd}\:{to}\:{both}\:{sides} \\ $$$${u}\left(\mathrm{1}\right)+\left({m}−\mathrm{1}\right){d}+{nd}={n}+{nd} \\ $$$${u}\left(\mathrm{1}\right)+\left({m}+{n}−\mathrm{1}\right){d}={n}+{n}\left(−\mathrm{1}\right) \\ $$$${u}\left(\mathrm{1}\right)+\left({m}+{n}−\mathrm{1}\right){d}=\mathrm{0} \\ $$$${u}\left({m}+{n}\right)=\mathrm{0} \\ $$$$ \\ $$$${u}\left(\mathrm{1}\right)+\left({m}−\mathrm{1}\right){d}={n} \\ $$$${Subtracting}\:\left({m}−{p}\right){d}\:{to}\:{both}\:{sides} \\ $$$${u}\left(\mathrm{1}\right)+\left({m}−\mathrm{1}\right){d}−\left({m}−{p}\right){d}={n}−\left({m}−{p}\right){d} \\ $$$${u}\left(\mathrm{1}\right)+\left({m}−\mathrm{1}−{m}+{p}\right){d}={n}−\left({m}−{p}\right)\left(−\mathrm{1}\right) \\ $$$${u}\left(\mathrm{1}\right)+\left({p}−\mathrm{1}\right){d}={n}+{m}−{p} \\ $$$${u}\left({p}\right)={m}+{n}−{p} \\ $$
Commented by Tawakalitu. last updated on 27/Aug/16
$${Thank}\:{you}\:{sir}.\:{i}\:{really}\:{appreciate} \\ $$
