Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 74013 by mathmax by abdo last updated on 17/Nov/19

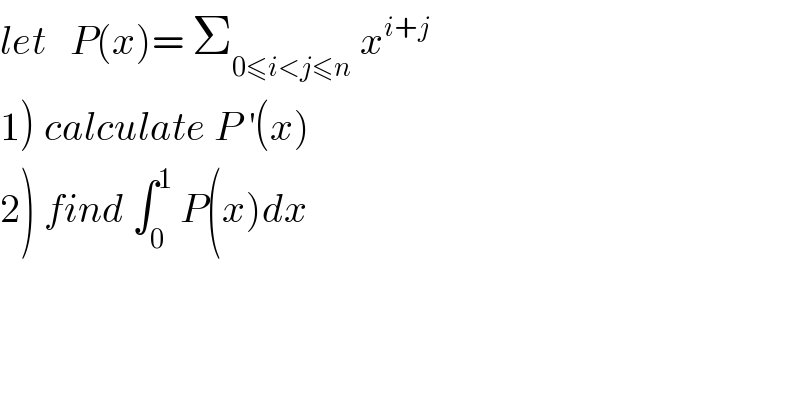
let P(x)= Σ_(0≤i<j≤n) x^(i+j) 1) calculate P^′ (x) 2) find ∫_0 ^1 P(x)dx

$${let}\:\:\:{P}\left({x}\right)=\:\sum_{\mathrm{0}\leqslant{i}<{j}\leqslant{n}} \:{x}^{{i}+{j}} \\ $$ $$\left.\mathrm{1}\right)\:{calculate}\:{P}\:^{'} \left({x}\right) \\ $$ $$\left.\mathrm{2}\right)\:{find}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{P}\left({x}\right){dx} \\ $$

Commented byabdomathmax last updated on 18/Nov/19

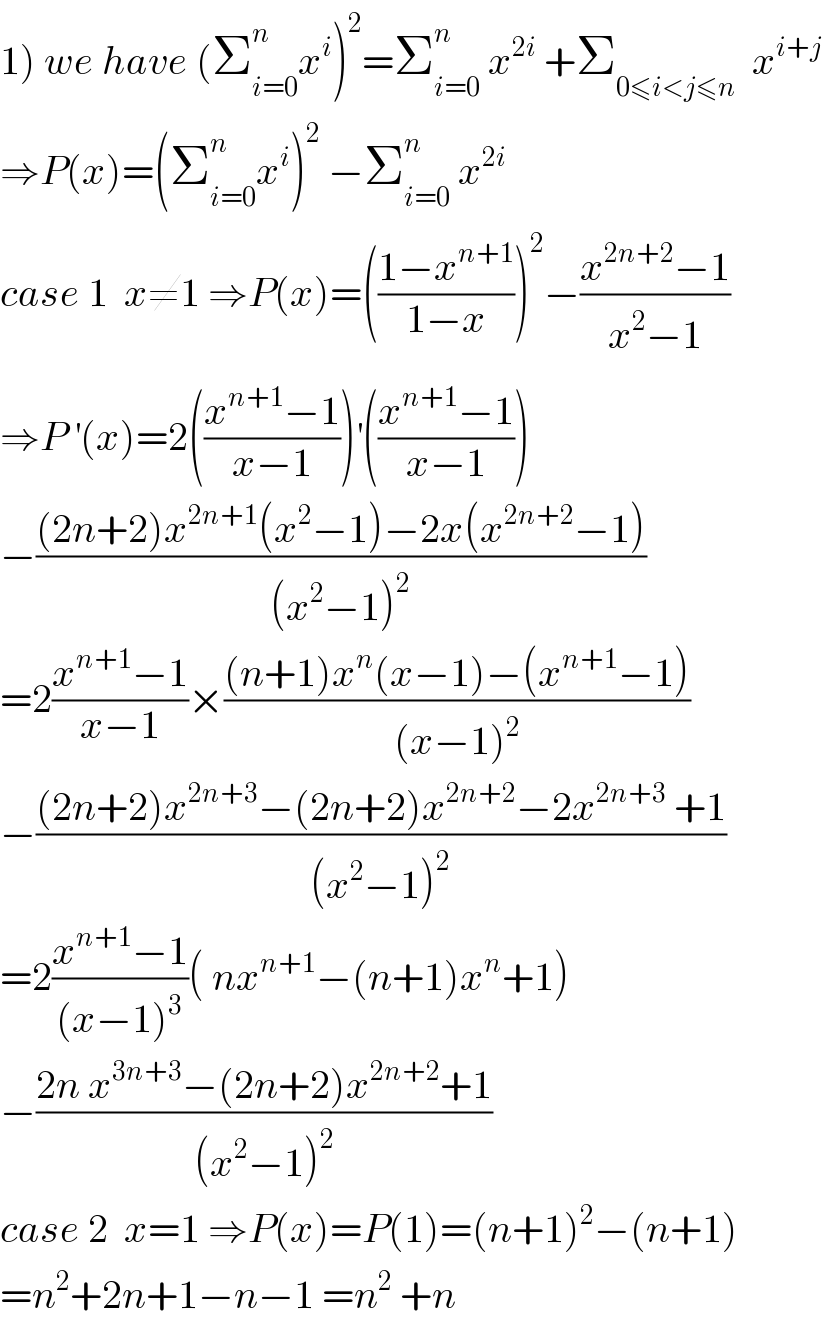
1) we have (Σ_(i=0) ^n x^i )^2 =Σ_(i=0) ^n x^(2i) +Σ_(0≤i<j≤n) x^(i+j) ⇒P(x)=(Σ_(i=0) ^(n ) x^i )^2 −Σ_(i=0) ^n x^(2i) case 1 x≠1 ⇒P(x)=(((1−x^(n+1) )/(1−x)))^2 −((x^(2n+2) −1)/(x^2 −1)) ⇒P^′ (x)=2(((x^(n+1) −1)/(x−1)))^′ (((x^(n+1) −1)/(x−1))) −(((2n+2)x^(2n+1) (x^2 −1)−2x(x^(2n+2) −1))/((x^2 −1)^2 )) =2((x^(n+1) −1)/(x−1))×(((n+1)x^n (x−1)−(x^(n+1) −1))/((x−1)^2 )) −(((2n+2)x^(2n+3) −(2n+2)x^(2n+2) −2x^(2n+3) +1)/((x^2 −1)^2 )) =2((x^(n+1) −1)/((x−1)^3 ))( nx^(n+1) −(n+1)x^n +1) −((2n x^(3n+3) −(2n+2)x^(2n+2) +1)/((x^2 −1)^2 )) case 2 x=1 ⇒P(x)=P(1)=(n+1)^2 −(n+1) =n^2 +2n+1−n−1 =n^2 +n

$$\left.\mathrm{1}\right)\:{we}\:{have}\:\left(\sum_{{i}=\mathrm{0}} ^{{n}} {x}^{{i}} \right)^{\mathrm{2}} =\sum_{{i}=\mathrm{0}} ^{{n}} \:{x}^{\mathrm{2}{i}} \:+\sum_{\mathrm{0}\leqslant{i}<{j}\leqslant{n}} \:\:{x}^{{i}+{j}} \\ $$ $$\Rightarrow{P}\left({x}\right)=\left(\sum_{{i}=\mathrm{0}} ^{{n}\:} {x}^{{i}} \right)^{\mathrm{2}} \:−\sum_{{i}=\mathrm{0}} ^{{n}} \:{x}^{\mathrm{2}{i}} \\ $$ $${case}\:\mathrm{1}\:\:{x}\neq\mathrm{1}\:\Rightarrow{P}\left({x}\right)=\left(\frac{\mathrm{1}−{x}^{{n}+\mathrm{1}} }{\mathrm{1}−{x}}\right)^{\mathrm{2}} −\frac{{x}^{\mathrm{2}{n}+\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{1}} \\ $$ $$\Rightarrow{P}\:^{'} \left({x}\right)=\mathrm{2}\left(\frac{{x}^{{n}+\mathrm{1}} −\mathrm{1}}{{x}−\mathrm{1}}\right)^{'} \left(\frac{{x}^{{n}+\mathrm{1}} −\mathrm{1}}{{x}−\mathrm{1}}\right) \\ $$ $$−\frac{\left(\mathrm{2}{n}+\mathrm{2}\right){x}^{\mathrm{2}{n}+\mathrm{1}} \left({x}^{\mathrm{2}} −\mathrm{1}\right)−\mathrm{2}{x}\left({x}^{\mathrm{2}{n}+\mathrm{2}} −\mathrm{1}\right)}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$ $$=\mathrm{2}\frac{{x}^{{n}+\mathrm{1}} −\mathrm{1}}{{x}−\mathrm{1}}×\frac{\left({n}+\mathrm{1}\right){x}^{{n}} \left({x}−\mathrm{1}\right)−\left({x}^{{n}+\mathrm{1}} −\mathrm{1}\right)}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$ $$−\frac{\left(\mathrm{2}{n}+\mathrm{2}\right){x}^{\mathrm{2}{n}+\mathrm{3}} −\left(\mathrm{2}{n}+\mathrm{2}\right){x}^{\mathrm{2}{n}+\mathrm{2}} −\mathrm{2}{x}^{\mathrm{2}{n}+\mathrm{3}} \:+\mathrm{1}}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$ $$=\mathrm{2}\frac{{x}^{{n}+\mathrm{1}} −\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{3}} }\left(\:{nx}^{{n}+\mathrm{1}} −\left({n}+\mathrm{1}\right){x}^{{n}} +\mathrm{1}\right) \\ $$ $$−\frac{\mathrm{2}{n}\:{x}^{\mathrm{3}{n}+\mathrm{3}} −\left(\mathrm{2}{n}+\mathrm{2}\right){x}^{\mathrm{2}{n}+\mathrm{2}} +\mathrm{1}}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$ $${case}\:\mathrm{2}\:\:{x}=\mathrm{1}\:\Rightarrow{P}\left({x}\right)={P}\left(\mathrm{1}\right)=\left({n}+\mathrm{1}\right)^{\mathrm{2}} −\left({n}+\mathrm{1}\right) \\ $$ $$={n}^{\mathrm{2}} +\mathrm{2}{n}+\mathrm{1}−{n}−\mathrm{1}\:={n}^{\mathrm{2}} \:+{n} \\ $$

Commented byabdomathmax last updated on 18/Nov/19

error of typo for x≠1 P^′ (x)=(((2x^(n+1) −2)(nx^(n+1) −(n+1)x^n +1))/((x−1)^3 )) −((2nx^(2n+3) −(2n+2)x^(2n+2) +1)/((x^2 −1)^2 ))

$${error}\:{of}\:{typo}\:{for}\:{x}\neq\mathrm{1} \\ $$ $${P}\:^{'} \left({x}\right)=\frac{\left(\mathrm{2}{x}^{{n}+\mathrm{1}} −\mathrm{2}\right)\left({nx}^{{n}+\mathrm{1}} −\left({n}+\mathrm{1}\right){x}^{{n}} +\mathrm{1}\right)}{\left({x}−\mathrm{1}\right)^{\mathrm{3}} } \\ $$ $$−\frac{\mathrm{2}{nx}^{\mathrm{2}{n}+\mathrm{3}} \:−\left(\mathrm{2}{n}+\mathrm{2}\right){x}^{\mathrm{2}{n}+\mathrm{2}} +\mathrm{1}}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$

Commented byabdomathmax last updated on 18/Nov/19

2) ∫_0 ^1 P(x)dx =Σ_(0≤i<j≤n) ∫_0 ^1 x^(i+j) dx =Σ_(0≤i<j≤n) (1/(i+j+1)) =Σ_(j=1) ^n (Σ_(i=0) ^(j−1) (1/(i+j+1))) changement of indice i+j+1=k give ∫_0 ^1 P(x)dx =Σ_(j=1) ^n (Σ_(k=j+1) ^(2j) (1/k)) =Σ_(j=1) ^n (Σ_(k=1) ^j (1/k) +Σ_(k=j+1) ^(2j) (1/k) −Σ_(k=1) ^j (1/k)) =Σ_(j=1) ^n ( H_(2j) −H_j ) =Σ_(j=1) ^n H_(2j) −Σ_(n=1) ^n H_j

$$\left.\mathrm{2}\right)\:\int_{\mathrm{0}} ^{\mathrm{1}} {P}\left({x}\right){dx}\:=\sum_{\mathrm{0}\leqslant{i}<{j}\leqslant{n}} \:\:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{i}+{j}} {dx} \\ $$ $$=\sum_{\mathrm{0}\leqslant{i}<{j}\leqslant{n}} \:\:\:\frac{\mathrm{1}}{{i}+{j}+\mathrm{1}} \\ $$ $$=\sum_{{j}=\mathrm{1}} ^{{n}} \left(\sum_{{i}=\mathrm{0}} ^{{j}−\mathrm{1}} \:\:\frac{\mathrm{1}}{{i}+{j}+\mathrm{1}}\right)\:{changement}\:{of}\:{indice} \\ $$ $${i}+{j}+\mathrm{1}={k}\:{give}\: \\ $$ $$\int_{\mathrm{0}} ^{\mathrm{1}} \:{P}\left({x}\right){dx}\:=\sum_{{j}=\mathrm{1}} ^{{n}} \left(\sum_{{k}={j}+\mathrm{1}} ^{\mathrm{2}{j}} \:\frac{\mathrm{1}}{{k}}\right) \\ $$ $$=\sum_{{j}=\mathrm{1}} ^{{n}} \left(\sum_{{k}=\mathrm{1}} ^{{j}} \frac{\mathrm{1}}{{k}}\:+\sum_{{k}={j}+\mathrm{1}} ^{\mathrm{2}{j}} \:\frac{\mathrm{1}}{{k}}\:\:−\sum_{{k}=\mathrm{1}} ^{{j}} \:\frac{\mathrm{1}}{{k}}\right) \\ $$ $$=\sum_{{j}=\mathrm{1}} ^{{n}} \left(\:{H}_{\mathrm{2}{j}} −{H}_{{j}} \right)\:=\sum_{{j}=\mathrm{1}} ^{{n}} \:{H}_{\mathrm{2}{j}} −\sum_{{n}=\mathrm{1}} ^{{n}} \:{H}_{{j}} \\ $$

Answered by mind is power last updated on 18/Nov/19

let Q(x)=(Σ_(i=0) ^n x^i ) Q(x)^2 =2p(x)+Σ_(i=1) ^n x^(2i) =2p(x) Q(x)=(((1−x^(n+1) )/(1−x)))^2 ,∀x∈C−{1} ⇒p(x)=(1/2)[(((1−x^(n+1) )/(1−x)))^2 −((1−x^(2n+2) )/(1−x^2 ))],∀x∈C−{1,−1} =p(x)=(1/2)[(((x^(2n+2) +1−2x^(n+1) )(1+x)−(1−x^(2n+2) )(1−x))/((1−x^2 )(1−x)))] ⇒p(x)=(1/2)[((x^(2n+3) +x−2x^(n+2) +x^(2n+2) +1−2x^(n+1) −1+x+x^(2n+2) −x^(2n+3) )/((1−x^2 )(1−x)))] ⇒p(x)=(1/2)[((2x^(2n+2) −2x^(n+2) −2x^(n+1) +2x)/((1−x^2 )(1−x)))] p(x)=((x^(2n+2) −x^(n+2) −x^(n+1) +x)/((1−x^2 )(1−x))) p′(x)=Σ_(1≤i<j≤n) (i+j)x^(i+j−1) =p′(x),x∈C−{1,−1} if x=1⇒p′(x)=Σ_(1≤i<j≤n) (i+j) =Σ_(2≤j≤n) Σ_(i=1) ^(j−1) (i+j) =Σ_(2≤j≤n) .{(((1+j+2j−1))/2).(j−1) =Σ_(2≤j≤n) (3/2)(j^2 −j)=(3/2).Σ_(2≤j≤n) j^2 −(3/2).((n−1)/2).(((n+2))/) =(3/2)[{.((n(n+1)(2n+1))/6)−(1/6)}−(((n−1)(n+2))/2) 2)∫_0 ^1 P(x)=Σ_(0≤i<j≤n) (1/(i+j+1)) =Σ_(j=1) ^n .Σ_(i=0) ^(j−1) .(1/(i+j+1)) =Σ_(j=1) ^n .Σ_(i=0) ^(j−1) .((1/(i+j+1))+Σ_(k=1) ^(j+i) (1/k)−Σ_(k=1) ^(j+i) (1/k)) =Σ_(j=1) ^n .Σ_(i=0) ^(j−1) {H_(2j) −H_(j+i) } =Σ_(j=1) ^n jH_(2j) −Σ_(j=1) ^n Σ_(i=0) ^(j−1) H_(i+j)

$$\mathrm{let}\:\mathrm{Q}\left(\mathrm{x}\right)=\left(\underset{\mathrm{i}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{x}^{\mathrm{i}} \right) \\ $$ $$\mathrm{Q}\left(\mathrm{x}\right)^{\mathrm{2}} =\mathrm{2p}\left(\mathrm{x}\right)+\underset{\mathrm{i}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{x}^{\mathrm{2i}} =\mathrm{2p}\left(\mathrm{x}\right) \\ $$ $$\mathrm{Q}\left(\mathrm{x}\right)=\left(\frac{\mathrm{1}−\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{1}−\mathrm{x}}\right)^{\mathrm{2}} ,\forall\mathrm{x}\in\mathbb{C}−\left\{\mathrm{1}\right\} \\ $$ $$\Rightarrow\mathrm{p}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left[\left(\frac{\mathrm{1}−\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{1}−\mathrm{x}}\right)^{\mathrm{2}} −\frac{\mathrm{1}−\mathrm{x}^{\mathrm{2n}+\mathrm{2}} }{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\right],\forall\mathrm{x}\in\mathbb{C}−\left\{\mathrm{1},−\mathrm{1}\right\} \\ $$ $$=\mathrm{p}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\left(\mathrm{x}^{\mathrm{2n}+\mathrm{2}} +\mathrm{1}−\mathrm{2x}^{\mathrm{n}+\mathrm{1}} \right)\left(\mathrm{1}+\mathrm{x}\right)−\left(\mathrm{1}−\mathrm{x}^{\mathrm{2n}+\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{x}\right)}{\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{x}\right)}\right] \\ $$ $$\Rightarrow\mathrm{p}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{x}^{\mathrm{2n}+\mathrm{3}} +\mathrm{x}−\mathrm{2x}^{\mathrm{n}+\mathrm{2}} +\mathrm{x}^{\mathrm{2n}+\mathrm{2}} +\mathrm{1}−\mathrm{2x}^{\mathrm{n}+\mathrm{1}} −\mathrm{1}+\mathrm{x}+\mathrm{x}^{\mathrm{2n}+\mathrm{2}} −\mathrm{x}^{\mathrm{2n}+\mathrm{3}} }{\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{x}\right)}\right] \\ $$ $$\Rightarrow\mathrm{p}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{2x}^{\mathrm{2n}+\mathrm{2}} −\mathrm{2x}^{\mathrm{n}+\mathrm{2}} −\mathrm{2x}^{\mathrm{n}+\mathrm{1}} +\mathrm{2x}}{\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{x}\right)}\right] \\ $$ $$\mathrm{p}\left(\mathrm{x}\right)=\frac{\mathrm{x}^{\mathrm{2n}+\mathrm{2}} −\mathrm{x}^{\mathrm{n}+\mathrm{2}} −\mathrm{x}^{\mathrm{n}+\mathrm{1}} +\mathrm{x}}{\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{x}\right)} \\ $$ $$\mathrm{p}'\left(\mathrm{x}\right)=\underset{\mathrm{1}\leqslant\mathrm{i}<\mathrm{j}\leqslant\mathrm{n}} {\sum}\left(\mathrm{i}+\mathrm{j}\right)\mathrm{x}^{\mathrm{i}+\mathrm{j}−\mathrm{1}} =\mathrm{p}'\left(\mathrm{x}\right),\mathrm{x}\in\mathbb{C}−\left\{\mathrm{1},−\mathrm{1}\right\} \\ $$ $$\mathrm{if}\:\mathrm{x}=\mathrm{1}\Rightarrow\mathrm{p}'\left(\mathrm{x}\right)=\underset{\mathrm{1}\leqslant\mathrm{i}<\mathrm{j}\leqslant\mathrm{n}} {\sum}\left(\mathrm{i}+\mathrm{j}\right) \\ $$ $$=\underset{\mathrm{2}\leqslant\mathrm{j}\leqslant\mathrm{n}} {\sum}\underset{\mathrm{i}=\mathrm{1}} {\overset{\mathrm{j}−\mathrm{1}} {\sum}}\left(\mathrm{i}+\mathrm{j}\right) \\ $$ $$=\underset{\mathrm{2}\leqslant\mathrm{j}\leqslant\mathrm{n}} {\sum}.\left\{\frac{\left(\mathrm{1}+\mathrm{j}+\mathrm{2j}−\mathrm{1}\right)}{\mathrm{2}}.\left(\mathrm{j}−\mathrm{1}\right)\right. \\ $$ $$=\underset{\mathrm{2}\leqslant\mathrm{j}\leqslant\mathrm{n}} {\sum}\frac{\mathrm{3}}{\mathrm{2}}\left(\mathrm{j}^{\mathrm{2}} −\mathrm{j}\right)=\frac{\mathrm{3}}{\mathrm{2}}.\underset{\mathrm{2}\leqslant\mathrm{j}\leqslant\mathrm{n}} {\sum}\:\mathrm{j}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{2}}.\frac{\mathrm{n}−\mathrm{1}}{\mathrm{2}}.\frac{\left(\mathrm{n}+\mathrm{2}\right)}{} \\ $$ $$=\frac{\mathrm{3}}{\mathrm{2}}\left[\left\{.\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{2n}+\mathrm{1}\right)}{\mathrm{6}}−\frac{\mathrm{1}}{\mathrm{6}}\right\}−\frac{\left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{n}+\mathrm{2}\right)}{\mathrm{2}}\right. \\ $$ $$\left.\mathrm{2}\right)\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{P}\left(\mathrm{x}\right)=\underset{\mathrm{0}\leqslant\mathrm{i}<\mathrm{j}\leqslant\mathrm{n}} {\sum}\frac{\mathrm{1}}{\mathrm{i}+\mathrm{j}+\mathrm{1}} \\ $$ $$=\underset{\mathrm{j}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}.\underset{\mathrm{i}=\mathrm{0}} {\overset{\mathrm{j}−\mathrm{1}} {\sum}}.\frac{\mathrm{1}}{\mathrm{i}+\mathrm{j}+\mathrm{1}} \\ $$ $$=\underset{\mathrm{j}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}.\underset{\mathrm{i}=\mathrm{0}} {\overset{\mathrm{j}−\mathrm{1}} {\sum}}.\left(\frac{\mathrm{1}}{\mathrm{i}+\mathrm{j}+\mathrm{1}}+\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{j}+\mathrm{i}} {\sum}}\frac{\mathrm{1}}{\mathrm{k}}−\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{j}+\mathrm{i}} {\sum}}\frac{\mathrm{1}}{\mathrm{k}}\right) \\ $$ $$=\underset{\mathrm{j}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}.\underset{\mathrm{i}=\mathrm{0}} {\overset{\mathrm{j}−\mathrm{1}} {\sum}}\left\{\mathrm{H}_{\mathrm{2j}} −\mathrm{H}_{\mathrm{j}+\mathrm{i}} \right\} \\ $$ $$=\underset{\mathrm{j}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{jH}_{\mathrm{2j}} −\underset{\mathrm{j}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\underset{\mathrm{i}=\mathrm{0}} {\overset{\mathrm{j}−\mathrm{1}} {\sum}}\mathrm{H}_{\mathrm{i}+\mathrm{j}} \\ $$ $$ \\ $$

Commented byabdomathmax last updated on 18/Nov/19

thank you sir ...

$${thank}\:{you}\:{sir}\:... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com