Previous in Relation and Functions Next in Relation and Functions
Question Number 74016 by mathmax by abdo last updated on 17/Nov/19
$${let}\:{g}\left({x}\right)\:=\frac{\mathrm{1}}{{x}}\int_{{x}} ^{\mathrm{2}{x}+\mathrm{1}} \:\:{arctan}\left({xt}\right){dt} \\ $$$${find}\:{lim}_{{x}\rightarrow\mathrm{0}} \:{g}\left({x}\right)\:\:{and}\:{lim}_{{x}\rightarrow+\infty} {g}\left({x}\right). \\ $$
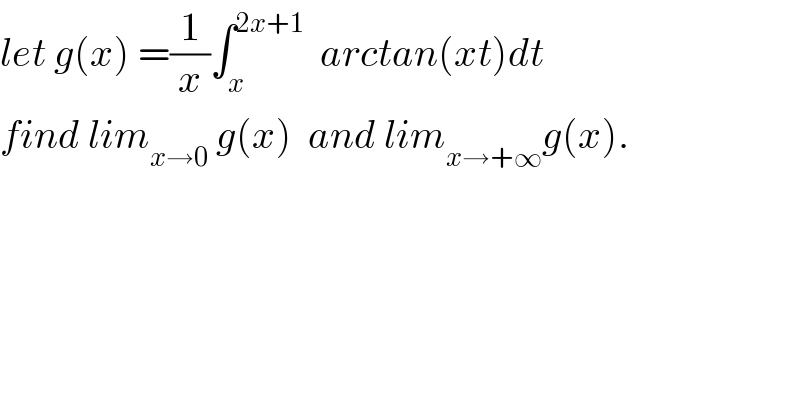
Commented by mathmax by abdo last updated on 18/Nov/19
![we have xg(x)=∫_x ^(2x+1) arctan(xt)dt =_(xt =u) ∫_x^2 ^(x(2x+1)) arctan(u)(du/x) =(1/x)∫_x^2 ^(2x^2 +x) arctan(u)du ⇒x^2 g(x)=_(by parts) [u arctan(u)]_x^2 ^(2x^2 +x) −∫_x^2 ^(2x^2 +x) (u/(1+u^2 ))du =(2x^2 +x)arctan(2x^2 +x)−x^2 arctan(x^2 )−[(1/2)ln(1+u^2 )]_x^2 ^(2x^2 +x) =(2x^2 +x)arctan(2x^2 +x)−x^2 arctan(x^2 ) −(1/2)ln(((1+(2x^2 +x)^2 )/(1+x^4 ))) ⇒ g(x)=(2+(1/x))arctan(2x^2 +x)−arctan(x^2 )−(1/(2x^2 ))ln(((1+4x^4 +4x^3 +x^2 )/(1+x^4 ))) g(x) ∼ (((2x+1)/x))(2x^2 +x)−x^2 −(1/(2x^2 ))ln(((4x^4 +4x^3 +x^2 +1)/(x^4 +1))) (x→0) lim_(x→0) g(x)=−∞ lim_(x→+∞) g(x)=2×(π/2)−(π/2)−0 =(π/2)](Q74047.png)
$${we}\:{have}\:{xg}\left({x}\right)=\int_{{x}} ^{\mathrm{2}{x}+\mathrm{1}} \:{arctan}\left({xt}\right){dt} \\ $$$$=_{{xt}\:={u}} \:\:\:\int_{{x}^{\mathrm{2}} } ^{{x}\left(\mathrm{2}{x}+\mathrm{1}\right)} \:{arctan}\left({u}\right)\frac{{du}}{{x}}\:=\frac{\mathrm{1}}{{x}}\int_{{x}^{\mathrm{2}} } ^{\mathrm{2}{x}^{\mathrm{2}} \:+{x}} \:\:{arctan}\left({u}\right){du} \\ $$$$\Rightarrow{x}^{\mathrm{2}} {g}\left({x}\right)=_{{by}\:{parts}} \:\:\:\left[{u}\:{arctan}\left({u}\right)\right]_{{x}^{\mathrm{2}} } ^{\mathrm{2}{x}^{\mathrm{2}} \:+{x}} −\int_{{x}^{\mathrm{2}} } ^{\mathrm{2}{x}^{\mathrm{2}} \:+{x}} \frac{{u}}{\mathrm{1}+{u}^{\mathrm{2}} }{du} \\ $$$$=\left(\mathrm{2}{x}^{\mathrm{2}} \:+{x}\right){arctan}\left(\mathrm{2}{x}^{\mathrm{2}} \:+{x}\right)−{x}^{\mathrm{2}} {arctan}\left({x}^{\mathrm{2}} \right)−\left[\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\right]_{{x}^{\mathrm{2}} } ^{\mathrm{2}{x}^{\mathrm{2}} \:+{x}} \\ $$$$=\left(\mathrm{2}{x}^{\mathrm{2}} \:+{x}\right){arctan}\left(\mathrm{2}{x}^{\mathrm{2}} \:+{x}\right)−{x}^{\mathrm{2}} \:{arctan}\left({x}^{\mathrm{2}} \right) \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\mathrm{1}+\left(\mathrm{2}{x}^{\mathrm{2}} \:+{x}\right)^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{4}} }\right)\:\Rightarrow \\ $$$${g}\left({x}\right)=\left(\mathrm{2}+\frac{\mathrm{1}}{{x}}\right){arctan}\left(\mathrm{2}{x}^{\mathrm{2}} \:+{x}\right)−{arctan}\left({x}^{\mathrm{2}} \right)−\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }{ln}\left(\frac{\mathrm{1}+\mathrm{4}{x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{3}} +{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{4}} }\right) \\ $$$${g}\left({x}\right)\:\sim\:\:\:\left(\frac{\mathrm{2}{x}+\mathrm{1}}{{x}}\right)\left(\mathrm{2}{x}^{\mathrm{2}} \:+{x}\right)−{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }{ln}\left(\frac{\mathrm{4}{x}^{\mathrm{4}} \:+\mathrm{4}{x}^{\mathrm{3}} \:+{x}^{\mathrm{2}} \:+\mathrm{1}}{{x}^{\mathrm{4}} \:+\mathrm{1}}\right)\:\left({x}\rightarrow\mathrm{0}\right) \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} {g}\left({x}\right)=−\infty \\ $$$${lim}_{{x}\rightarrow+\infty} {g}\left({x}\right)=\mathrm{2}×\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{2}}−\mathrm{0}\:=\frac{\pi}{\mathrm{2}} \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 18/Nov/19
$${g}\left({x}\right)=\left(\mathrm{2}+\frac{\mathrm{1}}{{x}}\right){arctan}\left(\mathrm{2}{x}^{\mathrm{2}} +{x}\right)−\frac{{arctan}\left({x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }{ln}\left(\frac{\mathrm{4}{x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{3}} \:+{x}^{\mathrm{2}} \:+\mathrm{1}}{{x}^{\mathrm{4}} \:+\mathrm{1}}\right) \\ $$
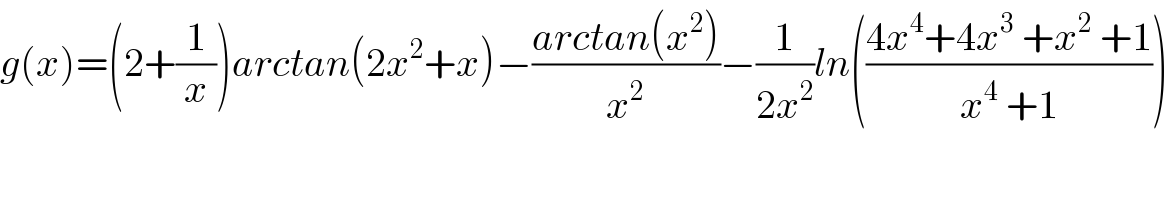
Commented by mind is power last updated on 18/Nov/19
$$\mathrm{ln}\left(\frac{\mathrm{1}+\mathrm{4x}^{\mathrm{4}} +\mathrm{4x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{4}} +\mathrm{1}}\right)=\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} +\mathrm{4x}^{\mathrm{3}} +\mathrm{4x}^{\mathrm{4}} \right)−\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{4}} \right) \\ $$$$\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} +\mathrm{4x}^{\mathrm{3}} +\mathrm{4x}^{\mathrm{4}} \right)−\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{4}} \right) \\ $$$$=\mathrm{x}^{\mathrm{2}} +\mathrm{0}\left(\mathrm{x}^{\mathrm{2}} \right)\:\:\:\mathrm{x}\rightarrow\mathrm{0} \\ $$$$ \\ $$
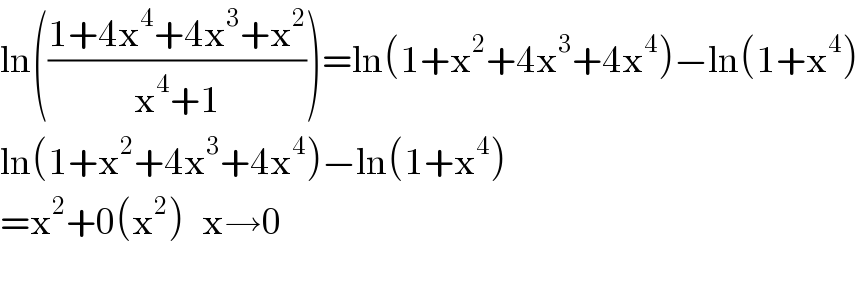
Commented by abdomathmax last updated on 18/Nov/19
$${this}\:{quantity}\:{is}\:{multiplied}\:{by}\:−\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }\:{sir}\:.... \\ $$
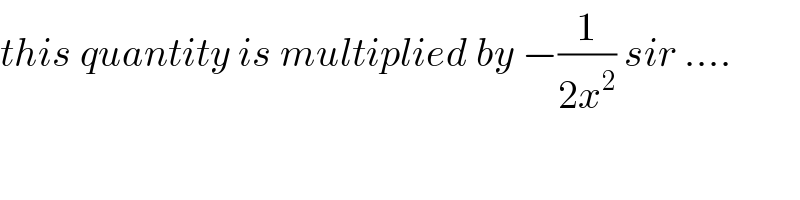
Commented by mind is power last updated on 19/Nov/19
$${yeah}\:{so}\:{lim}−\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }\:\:\:\:\:{ln}\frac{\left(\mathrm{1}+\mathrm{4}{x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{3}} +{x}^{\mathrm{2}} \right)}{{x}^{\mathrm{4}} +\mathrm{1}}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by mind is power last updated on 18/Nov/19
![∫arctan(xt)dt,u=xt =(1/x)∫arctan(u)du =(1/x)[uarctab(u)]−(1/x)∫(u/(1+u^2 ))du =(1/x)[u arcran(u)]−(1/(2x)).ln(1+u^2 ) g(x)=(1/x^2 ).(x(2x+1)arctan(x(2x+1))−((ln(1+x^2 (2x+1)^2 ))/2)−x^2 arctan(x^2 )+((ln(1+x^4 ))/2)} lim_(x→0) g(x)= ln(1+t)=t+o(t) arctan(t)=t+o(t) ⇒lim_(x→0) g(x)=(1−(1/2)−0+0)=(1/2) lim_(x→+∞) g(x)=π−(π/2)=(π/2)](Q74032.png)
$$\int\mathrm{arctan}\left(\mathrm{xt}\right)\mathrm{dt},\mathrm{u}=\mathrm{xt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{x}}\int\mathrm{arctan}\left(\mathrm{u}\right)\mathrm{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{x}}\left[\mathrm{uarctab}\left(\mathrm{u}\right)\right]−\frac{\mathrm{1}}{\mathrm{x}}\int\frac{\mathrm{u}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\mathrm{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{x}}\left[\mathrm{u}\:\mathrm{arcran}\left(\mathrm{u}\right)\right]−\frac{\mathrm{1}}{\mathrm{2x}}.\mathrm{ln}\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right) \\ $$$$\mathrm{g}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }.\left(\mathrm{x}\left(\mathrm{2x}+\mathrm{1}\right)\mathrm{arctan}\left(\mathrm{x}\left(\mathrm{2x}+\mathrm{1}\right)\right)−\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \left(\mathrm{2x}+\mathrm{1}\right)^{\mathrm{2}} \right)}{\mathrm{2}}−\mathrm{x}^{\mathrm{2}} \mathrm{arctan}\left(\mathrm{x}^{\mathrm{2}} \right)+\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{4}} \right)}{\mathrm{2}}\right\} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{g}\left(\mathrm{x}\right)= \\ $$$$\mathrm{ln}\left(\mathrm{1}+\mathrm{t}\right)=\mathrm{t}+\mathrm{o}\left(\mathrm{t}\right) \\ $$$$\mathrm{arctan}\left(\mathrm{t}\right)=\mathrm{t}+\mathrm{o}\left(\mathrm{t}\right) \\ $$$$\Rightarrow\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{g}\left(\mathrm{x}\right)=\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{0}+\mathrm{0}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}g}\left(\mathrm{x}\right)=\pi−\frac{\pi}{\mathrm{2}}=\frac{\pi}{\mathrm{2}} \\ $$$$ \\ $$
Commented by abdomathmax last updated on 18/Nov/19
$${thank}\:{you}\:{sir}. \\ $$
Commented by mind is power last updated on 18/Nov/19
$$\hat {\mathrm{y}}'\mathrm{re}\:\mathrm{welcom} \\ $$