
Question and Answers Forum
Question Number 74322 by naka3546 last updated on 22/Nov/19
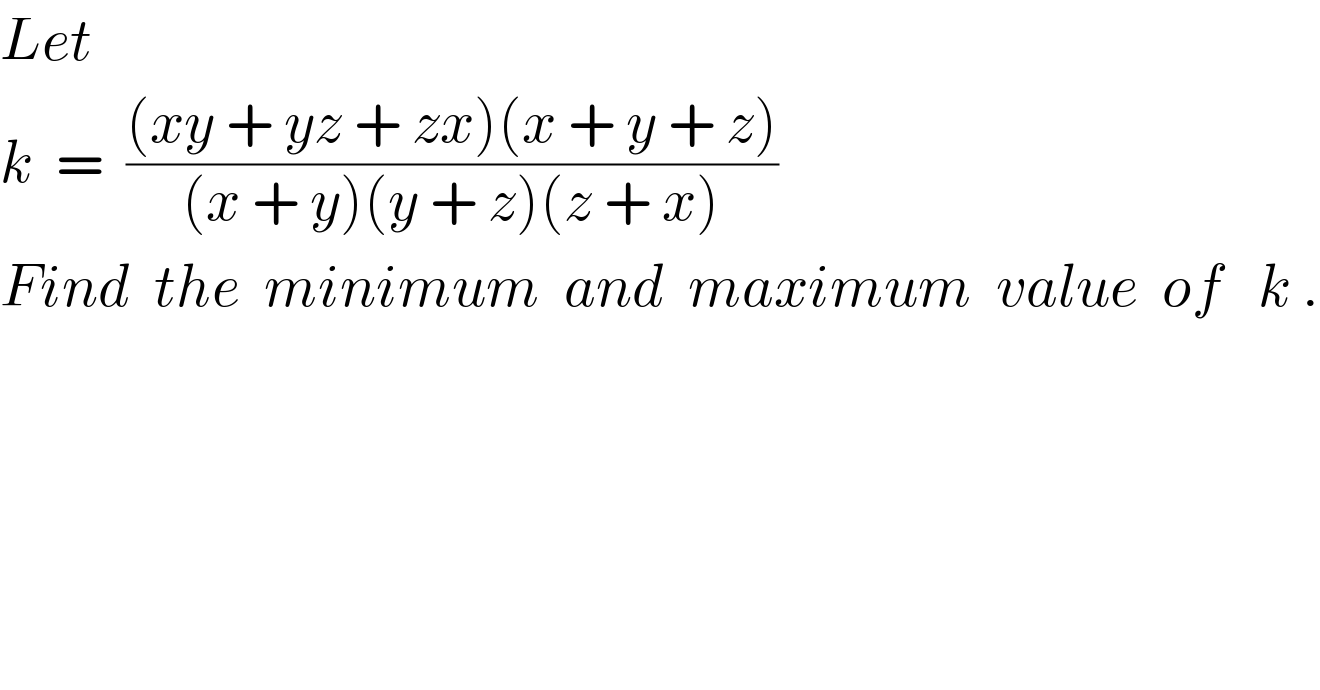
$${Let}\:\: \\ $$$${k}\:\:=\:\:\frac{\left({xy}\:+\:{yz}\:+\:{zx}\right)\left({x}\:+\:{y}\:+\:{z}\right)}{\left({x}\:+\:{y}\right)\left({y}\:+\:{z}\right)\left({z}\:+\:{x}\right)} \\ $$$${Find}\:\:{the}\:\:{minimum}\:\:{and}\:\:{maximum}\:\:{value}\:\:{of}\:\:\:{k}\:. \\ $$
Answered by MJS last updated on 23/Nov/19
![k−1=((xyz)/((x+y)(x+z)(y+z))) y=px∧z=qx (1) k−1=((pq)/((p+1)(p+q)(q+1))) (d/dq)[((pq)/((p+1)(p+q)(q+1)))]=0 ((p(p−q^2 ))/((p+1)(p+q)^2 (q+1)^2 ))=0 ⇒ q=±(√p) insert in (1) k−1=(p/((1±(√p))^2 (p+1))) (d/dp)[(p/((1±(√p))^2 (p+1)))]=0 ((1±p^(3/2) )/((1∓(√p))^3 (p+1)^2 ))=0 ⇒ p=1∧q=1 (no other real solution) ⇒x=y=z ⇒ k−1=(1/8) ⇒ k=(9/8) which is the absolute maximum the minimum is −∞ put q=1: k−1=(p/(2(p+1)^2 )) lim_(p→−1) ((p/(2(p+1)^2 ))) =−∞](Q74375.png)
$${k}−\mathrm{1}=\frac{{xyz}}{\left({x}+{y}\right)\left({x}+{z}\right)\left({y}+{z}\right)} \\ $$$${y}={px}\wedge{z}={qx} \\ $$$$\left(\mathrm{1}\right)\:\:{k}−\mathrm{1}=\frac{{pq}}{\left({p}+\mathrm{1}\right)\left({p}+{q}\right)\left({q}+\mathrm{1}\right)} \\ $$$$\frac{{d}}{{dq}}\left[\frac{{pq}}{\left({p}+\mathrm{1}\right)\left({p}+{q}\right)\left({q}+\mathrm{1}\right)}\right]=\mathrm{0} \\ $$$$\frac{{p}\left({p}−{q}^{\mathrm{2}} \right)}{\left({p}+\mathrm{1}\right)\left({p}+{q}\right)^{\mathrm{2}} \left({q}+\mathrm{1}\right)^{\mathrm{2}} }=\mathrm{0} \\ $$$$\Rightarrow\:{q}=\pm\sqrt{{p}} \\ $$$$\mathrm{insert}\:\mathrm{in}\:\left(\mathrm{1}\right) \\ $$$${k}−\mathrm{1}=\frac{{p}}{\left(\mathrm{1}\pm\sqrt{{p}}\right)^{\mathrm{2}} \left({p}+\mathrm{1}\right)} \\ $$$$\frac{{d}}{{dp}}\left[\frac{{p}}{\left(\mathrm{1}\pm\sqrt{{p}}\right)^{\mathrm{2}} \left({p}+\mathrm{1}\right)}\right]=\mathrm{0} \\ $$$$\frac{\mathrm{1}\pm{p}^{\frac{\mathrm{3}}{\mathrm{2}}} }{\left(\mathrm{1}\mp\sqrt{{p}}\right)^{\mathrm{3}} \left({p}+\mathrm{1}\right)^{\mathrm{2}} }=\mathrm{0} \\ $$$$\Rightarrow\:{p}=\mathrm{1}\wedge{q}=\mathrm{1} \\ $$$$\left(\mathrm{no}\:\mathrm{other}\:\mathrm{real}\:\mathrm{solution}\right) \\ $$$$\Rightarrow{x}={y}={z} \\ $$$$\Rightarrow\:{k}−\mathrm{1}=\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\Rightarrow\:{k}=\frac{\mathrm{9}}{\mathrm{8}} \\ $$$$\mathrm{which}\:\mathrm{is}\:\mathrm{the}\:\mathrm{absolute}\:\mathrm{maximum} \\ $$$$\mathrm{the}\:\mathrm{minimum}\:\mathrm{is}\:−\infty \\ $$$$\mathrm{put}\:{q}=\mathrm{1}: \\ $$$${k}−\mathrm{1}=\frac{{p}}{\mathrm{2}\left({p}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\underset{{p}\rightarrow−\mathrm{1}} {\mathrm{lim}}\left(\frac{{p}}{\mathrm{2}\left({p}+\mathrm{1}\right)^{\mathrm{2}} }\right)\:=−\infty \\ $$
