Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 74394 by aliesam last updated on 23/Nov/19

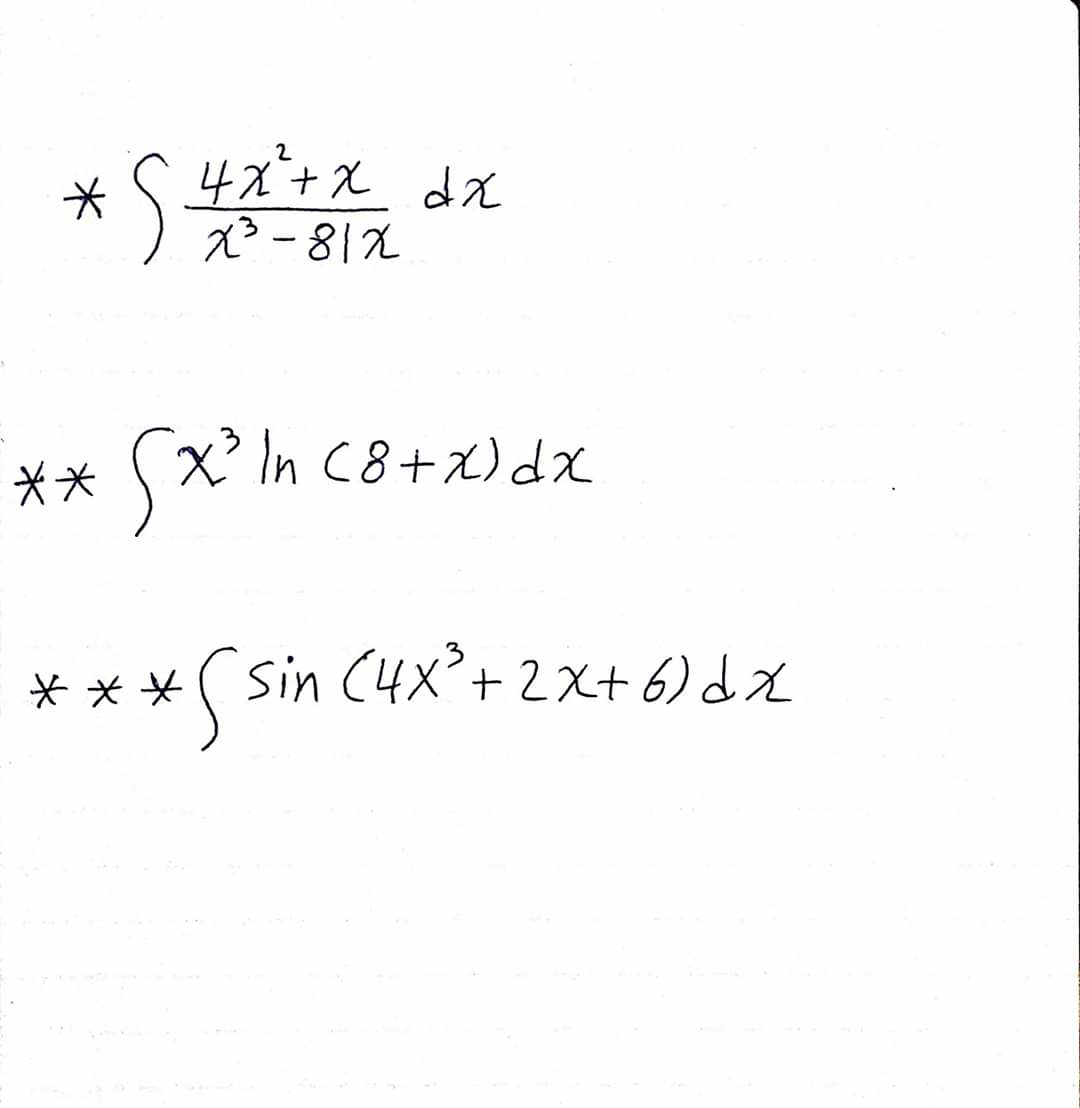
Commented by mathmax by abdo last updated on 23/Nov/19

$$1)letdecomposeF\left(x\right)=\frac{4x^2+x}{x^3-81x}\Rightarrow F\left(x\right)=\frac{4x^2+x}{x(x-9)(x+9)}$$$$=\frac{4x+1}{(x-9)(x+9)}=\frac{a}{x-9}+\frac{b}{x+9}$$$$a=(x-9)F\left(x\right){\mid }_{x=9}=\frac{37}{18}$$$$b=(x+9)F\left(x\right){\mid }_{x=-9}=\frac{-35}{-18}=\frac{35}{18}\Rightarrow F\left(x\right)=\frac{37}{18(x-9)}+\frac{35}{18(x+9)}\Rightarrow$$$$\int \frac{4x^2+x}{x^3-81x}dx=\int F\left(x\right)dx=\frac{37}{18}ln\mid x-9\mid +\frac{35}{18}ln\mid x+9\mid +C.$$

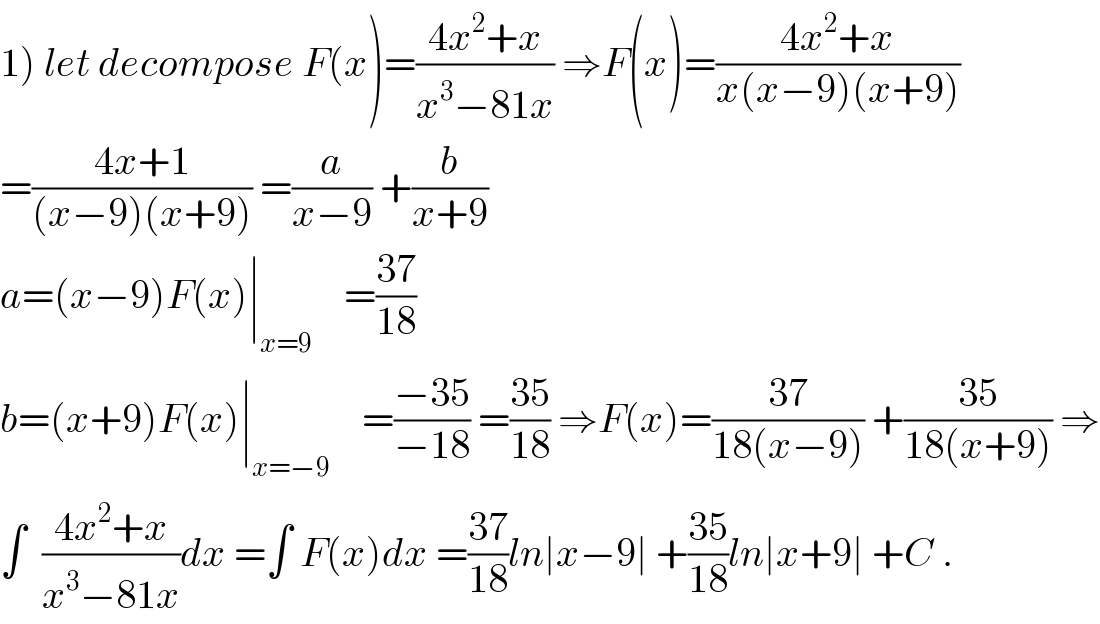
Commented by mathmax by abdo last updated on 23/Nov/19

$$letA=\int x^{3}ln(x+8)dx\Rightarrow A{=}_{x+8=t}\int {(t-8)}^{3}ln\left(t\right)dt$$$$=\int (t^3+3t^2.8+3t.8^2+8^3)ln\left(t\right)dt$$$$=\int t^{3}ln\left(t\right)dt+24\int t^{2}ln\left(t\right)dt+192\int tln\left(t\right)dt+512\int ln\left(t\right)dt$$$$\int lntdt=tlnt-t+c_1$$$$\int tln\left(t\right)dt{=}_{bypsrts}\frac{t^2}{2}lnt-\int \frac{t^2}{2}\frac{dt}{t}=\frac{t^{2}lnt}{2}-\frac{1}{2}\int tdt$$$$=\frac{t^{2}lnt}{2}-\frac{t^2}{4}+c_2$$$$\int t^{2}ln\left(t\right)dt=\frac{t^{3}ln\left(t\right)}{3}-\int \frac{t^3}{3}\frac{dt}{t}=\frac{t^{3}ln\left(t\right)}{3}-\frac{1}{3}\int t^{2}dt$$$$=\frac{t^{3}ln\left(t\right)}{3}-\frac{1}{9}{t}^3+c_3$$$$\int t^{3}ln\left(t\right)dt=\frac{t^{4}ln\left(t\right)}{4}-\int \frac{t^4}{4}\frac{dt}{t}=\frac{t^{4}ln\left(t\right)}{4}-\frac{1}{16}{t}^4+c_4\Rightarrow$$$$A=\frac{{(x+8)}^{4}ln(x+8)}{4}-\frac{1}{16}{(x+8)}^4+8{(x+8)}^{3}ln(x+8)-\frac{8}{3}{(x+8)}^3$$$$+192\{\frac{{(x+8)}^{2}ln(x+8)}{2}-\frac{{(x+8)}^2}{4}\}+512\{(x+8)ln(x+8)-(x+8)\}+C$$

Commented by ~blr237~ last updated on 23/Nov/19

$$f\left(x\right)=\int x^{3}ln(8+x)dx$$$$bypartwehave{u}^{\prime }=x^3\to u=\frac{1}{4}{x}^4-\frac{8^4}{4}$$$$andv=ln(8+x)\to v^{\prime }=\frac{1}{8+x}$$$$f\left(x\right)=\left[\left(\frac{x^4-8^4}{4}\right)ln(8+x)\right]-\frac{1}{4}{\int }^{}\frac{x^4-8^4}{x-(-8)}dx$$$$=\left(\frac{x^4-8^4}{4}\right)ln(8+x)-\frac{1}{4}\int \frac{8^4}{8}[1+(-\frac{x}{8})+{(-\frac{x}{8})}^2+{\left(\frac{-x}{8}\right)}^{3}dx$$$$=\left(\frac{x^4-8^4}{4}\right)ln(8+x)-4^5[x-\frac{x^2}{16}+\frac{x^3}{3\times 64}-\frac{x^4}{4\times 8^3}]+c$$$$So$$$$f\left(x\right)=\left(\frac{x^4-8^4}{4}\right)ln(8+x)-4^{5}x+4^3{x}^2-\frac{4^2{x}^3}{3}+\frac{x^4}{4}+c$$$$$$

Commented by MJS last updated on 24/Nov/19

$$\mathrm{I}{\mathrm{don}}^{\prime }\mathrm{t}\mathrm{think}\mathrm{we}\mathrm{can}\mathrm{solve}\mathrm{the}{3}^{\mathrm{rd}}\mathrm{one}$$

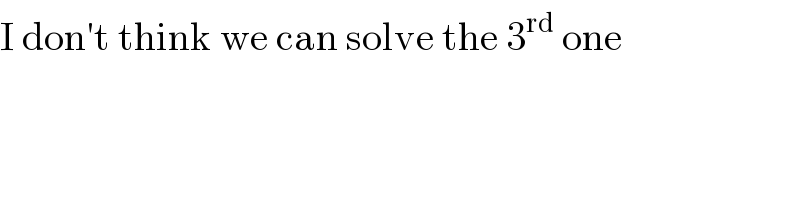
Answered by MJS last updated on 23/Nov/19

$$\ast$$$$\int \frac{4x^2+x}{x^3-81x}dx=\int \frac{4x+1}{x^2-81}dx=$$$$=\frac{37}{18}\int \frac{dx}{x-9}+\frac{35}{18}\int \frac{dx}{x+9}=$$$$=\frac{37}{18}\ln (x-9)+\frac{35}{18}\ln (x+9)+C$$$$$$$$\ast \ast$$$$\int x^3\ln (x+8)dx=$$$$[u^{\prime }=x^3\Rightarrow u=\frac{1}{4}{x}^4;v=\ln (x+8)\Rightarrow v^{\prime }=\frac{1}{x+8}]$$$$=\frac{1}{4}{x}^4\ln (x+8)-\frac{1}{4}\int \frac{x^4}{x+8}dx=$$$$$$$$\int \frac{x^4}{x+8}dx=\int (x^3-8x^2+64x-512+\frac{4096}{x+8})dx=$$$$=\frac{1}{4}{x}^4-\frac{8}{3}{x}^3+32x^2-512x+4096\ln (x+8)$$$$$$$$=-\frac{x(3x^3-32x^2+384x-6144)}{48}+(\frac{1}{4}{x}^4-1024)\ln (x+8)+C$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com