
Question Number 74526 by Kunal12588 last updated on 25/Nov/19
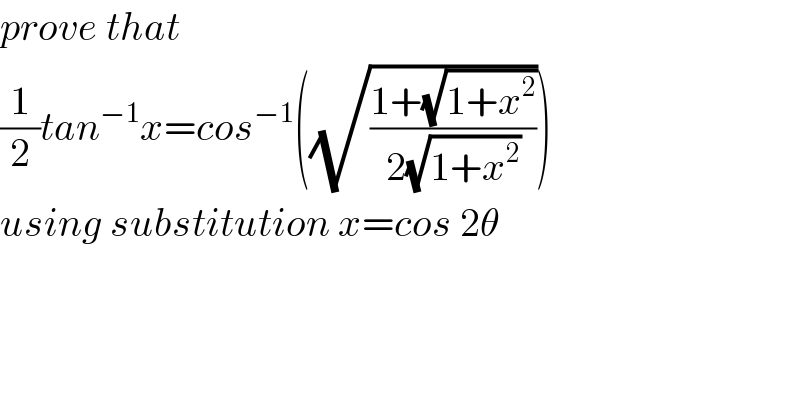
$${prove}\:{that} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{tan}^{−\mathrm{1}} {x}={cos}^{−\mathrm{1}} \left(\sqrt{\frac{\mathrm{1}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{\mathrm{2}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}}\right) \\ $$$${using}\:{substitution}\:{x}={cos}\:\mathrm{2}\theta \\ $$
Answered by mind is power last updated on 25/Nov/19
![miss click i think is x=tg(2θ) true for x≥0 x=−1 tan^− (−1)=−(π/4) we get −(π/8) cos^− (x)∈[0,π] since t→tg(2θ) is bjection I=]0,(π/4)[→R^+ ⇒ ∀x∈R ∃! θ∈I ∣ x=tg(2θ) tan^(−1) (tg(2θ))=2θ since 2θ∈]0,(π/2)[ lHs =θ 1+x^2 =(1/(cos^2 (2θ)))⇒(√(1+x^2 ))=(1/(cos(2θ))),since cos(2θ)≥0 over I (√((1+(√(1+x^2 )))/(2(√(1+x^2 )))))=(√((1+(1/(cos(2θ))))/(2/(cos(2θ)))))=(√((1+cos(2θ))/2)) 1+cos(2θ)=2cos^2 (θ)⇒(√((2cos^2 (θ))/2))=∣cos(θ)∣=cos(θ) cos^− (cos(θ))=θ cause θ∈]0,(π/4)[ so θ=θ this ⇒∀x≥0 ((tan^− (x))/2)=cos^(−1) (((√(1+(√(1+x^2 ))))/(2(√(1+x^2 )))))](Q74530.png)
$${miss}\:{click} \\ $$$${i}\:{think}\:{is}\:{x}={tg}\left(\mathrm{2}\theta\right) \\ $$$${true}\:{for}\:{x}\geqslant\mathrm{0} \\ $$$${x}=−\mathrm{1}\:\:{tan}^{−} \left(−\mathrm{1}\right)=−\frac{\pi}{\mathrm{4}} \\ $$$${we}\:{get}\:−\frac{\pi}{\mathrm{8}} \\ $$$${cos}^{−} \left({x}\right)\in\left[\mathrm{0},\pi\right] \\ $$$${since}\:\:{t}\rightarrow{tg}\left(\mathrm{2}\theta\right)\:{is}\:{bjection}\: \\ $$$$\left.{I}=\right]\mathrm{0},\frac{\pi}{\mathrm{4}}\left[\rightarrow\mathbb{R}^{+} \right. \\ $$$$\Rightarrow\:\forall{x}\in\mathbb{R}\:\exists!\:\:\theta\in{I}\:\:\mid\:\:{x}={tg}\left(\mathrm{2}\theta\right) \\ $$$$\left.\mathrm{tan}^{−\mathrm{1}} \left({tg}\left(\mathrm{2}\theta\right)\right)=\mathrm{2}\theta\:\:\:{since}\:\mathrm{2}\theta\in\right]\mathrm{0},\frac{\pi}{\mathrm{2}}\left[\right. \\ $$$${lHs}\:=\theta \\ $$$$\mathrm{1}+{x}^{\mathrm{2}} =\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \left(\mathrm{2}\theta\right)}\Rightarrow\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }=\frac{\mathrm{1}}{{cos}\left(\mathrm{2}\theta\right)},{since}\:{cos}\left(\mathrm{2}\theta\right)\geqslant\mathrm{0}\:\:{over}\:{I} \\ $$$$\sqrt{\frac{\mathrm{1}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{\mathrm{2}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}}=\sqrt{\frac{\mathrm{1}+\frac{\mathrm{1}}{{cos}\left(\mathrm{2}\theta\right)}}{\frac{\mathrm{2}}{{cos}\left(\mathrm{2}\theta\right)}}}=\sqrt{\frac{\mathrm{1}+{cos}\left(\mathrm{2}\theta\right)}{\mathrm{2}}} \\ $$$$\mathrm{1}+{cos}\left(\mathrm{2}\theta\right)=\mathrm{2}{cos}^{\mathrm{2}} \left(\theta\right)\Rightarrow\sqrt{\frac{\mathrm{2}{cos}^{\mathrm{2}} \left(\theta\right)}{\mathrm{2}}}=\mid{cos}\left(\theta\right)\mid={cos}\left(\theta\right) \\ $$$$\left.{cos}^{−} \left({cos}\left(\theta\right)\right)=\theta\:\:{cause}\:\theta\in\right]\mathrm{0},\frac{\pi}{\mathrm{4}}\left[\right. \\ $$$${so}\:\theta=\theta\:\:\:{this}\:\Rightarrow\forall{x}\geqslant\mathrm{0}\:\:\frac{{tan}^{−} \left({x}\right)}{\mathrm{2}}=\mathrm{cos}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}}{\mathrm{2}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right) \\ $$
