
Question and Answers Forum
Question Number 74614 by chess1 last updated on 27/Nov/19
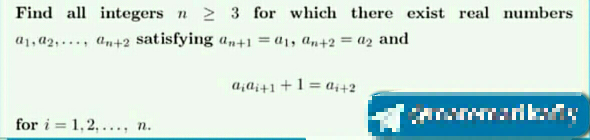
Answered by mind is power last updated on 27/Nov/19
![we can extend without and U_(i+n) =a_i ,∀i∈[1,n] U_i .U_(i+1) +1=U_(i+2) ⇒a_(n+3) =a_3 ,if a_1 ,.......a_n the sequence U_n exist since is (a_(1,) ,a_2 ,.....a_n )is repeted infintly times if U_n exist ⇒a_i existe tack just n+2 first therm so we can extend a_i without lost a_(i+1) a_i +1=a_(i+2) { ((a_(i+2) a_(i+1) +1=a_(i+3) ......1)),((a_i a_(i+1) +1=a_(i+2) ...2)) :} 1∗a_i −..2∗a_(i+2) ⇒a_i a_(i+3) −a_(i+2) ^2 =a_i −a_(i+2) Σ_(i=1) ^n (a_i a_(i+3) −a_(i+2) ^2 )=Σ_(i=1) ^n a_i −a_(i+2) =a_1 +a_2 −a_(n+2) −a_(n+1) =0 ⇒Σ_(i=1) ^n (a_i a_(i+3) −a_(i+2) ^2 )=0...E Σ_(i=1) ^n a_(i+2) =Σ_(k=1) ^n a_k ^2 ,since a_(n+1) =a_1 &a_(n+2) =a_2 ⇒E⇔Σ_(k=1) ^n (a_k a_(k+3) −a_k ^2 )=0 Σ_(k=1) ^n a_(k+3) ^2 =Σ_(k=1) ^n a_k ^2 −a_3 ^2 +a_(n+3) ^2 ,withe our expended series =Σ_(k=1) ^n a_k ^2 ⇒E⇔2Σ_(k=1) ^n a_k a_(k+3) −2Σ_(k=1) ^n a_k ^2 =0 ⇒Σ_(k=1) ^n (a_k ^2 +a_(k+3) ^2 −2a_k a_(k+3) )=0⇒Σ_(k=1) ^n (a_(k+3) −a_k )^2 ⇒∀k∈[0,n] a_(k+3) =a_k ⇒ 3∣n if periode 1 ⇒a_3 =a_2 =a_1 ⇒a_1 ^2 +1=a_1 since X^2 −X+1=0has non solution overR ⇒a_n can not constante for n=3 (−1,−1,2)=(a_1 ,a_2 ,a_3 ) worcks a_4 =−1=a_(3+1) =a_1 a_5 =−1.2+1=−1=a_(3+2) =a_2 the smalest periodicity is 3](Q74626.png)
Commented by chess1 last updated on 27/Nov/19

| ||
Question and Answers Forum | ||
Question Number 74614 by chess1 last updated on 27/Nov/19 | ||
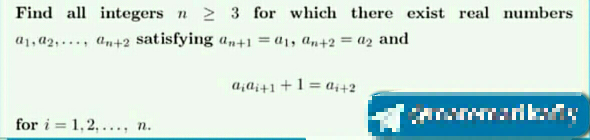 | ||
Answered by mind is power last updated on 27/Nov/19 | ||
![we can extend without and U_(i+n) =a_i ,∀i∈[1,n] U_i .U_(i+1) +1=U_(i+2) ⇒a_(n+3) =a_3 ,if a_1 ,.......a_n the sequence U_n exist since is (a_(1,) ,a_2 ,.....a_n )is repeted infintly times if U_n exist ⇒a_i existe tack just n+2 first therm so we can extend a_i without lost a_(i+1) a_i +1=a_(i+2) { ((a_(i+2) a_(i+1) +1=a_(i+3) ......1)),((a_i a_(i+1) +1=a_(i+2) ...2)) :} 1∗a_i −..2∗a_(i+2) ⇒a_i a_(i+3) −a_(i+2) ^2 =a_i −a_(i+2) Σ_(i=1) ^n (a_i a_(i+3) −a_(i+2) ^2 )=Σ_(i=1) ^n a_i −a_(i+2) =a_1 +a_2 −a_(n+2) −a_(n+1) =0 ⇒Σ_(i=1) ^n (a_i a_(i+3) −a_(i+2) ^2 )=0...E Σ_(i=1) ^n a_(i+2) =Σ_(k=1) ^n a_k ^2 ,since a_(n+1) =a_1 &a_(n+2) =a_2 ⇒E⇔Σ_(k=1) ^n (a_k a_(k+3) −a_k ^2 )=0 Σ_(k=1) ^n a_(k+3) ^2 =Σ_(k=1) ^n a_k ^2 −a_3 ^2 +a_(n+3) ^2 ,withe our expended series =Σ_(k=1) ^n a_k ^2 ⇒E⇔2Σ_(k=1) ^n a_k a_(k+3) −2Σ_(k=1) ^n a_k ^2 =0 ⇒Σ_(k=1) ^n (a_k ^2 +a_(k+3) ^2 −2a_k a_(k+3) )=0⇒Σ_(k=1) ^n (a_(k+3) −a_k )^2 ⇒∀k∈[0,n] a_(k+3) =a_k ⇒ 3∣n if periode 1 ⇒a_3 =a_2 =a_1 ⇒a_1 ^2 +1=a_1 since X^2 −X+1=0has non solution overR ⇒a_n can not constante for n=3 (−1,−1,2)=(a_1 ,a_2 ,a_3 ) worcks a_4 =−1=a_(3+1) =a_1 a_5 =−1.2+1=−1=a_(3+2) =a_2 the smalest periodicity is 3](Q74626.png) | ||
| ||
Commented by chess1 last updated on 27/Nov/19 | ||
 | ||