
Question and Answers Forum
Question Number 74793 by mathmax by abdo last updated on 30/Nov/19
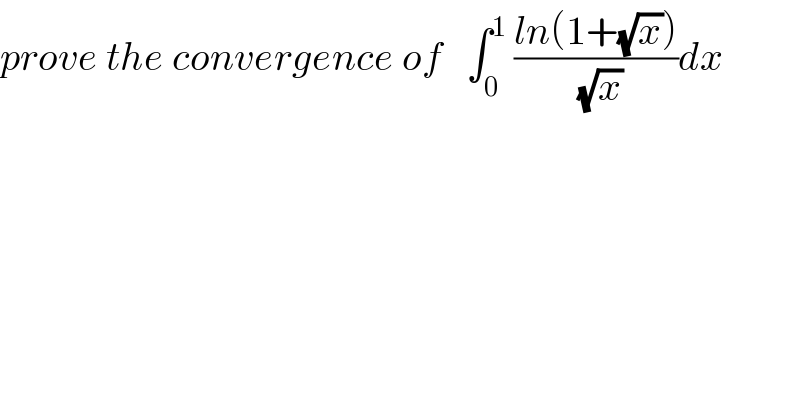
Commented by mathmax by abdo last updated on 06/Dec/19
![I=∫_0 ^1 ((ln(1+(√x)))/(√x))dx changement (√x)=t give x=t^2 ⇒ I =∫_0 ^1 ((ln(1+t))/t)(2t)dt =2 ∫_0 ^1 ln(1+t)dt =_(1+t=u) 2∫_1 ^2 ln(u)du =2[ulnu−u]_1 ^2 =2{2ln(2)−2+1} =4ln(2)−2](Q75057.png)
Answered by mind is power last updated on 01/Dec/19
![u=(√x)⇒du=(1/(2(√x)))dx ∫_0 ^1 2ln(1+u)du=[2(u+1)ln(u+1)−2u]_0 ^1 =4ln(2)−2](Q74815.png)
| ||
Question and Answers Forum | ||
Question Number 74793 by mathmax by abdo last updated on 30/Nov/19 | ||
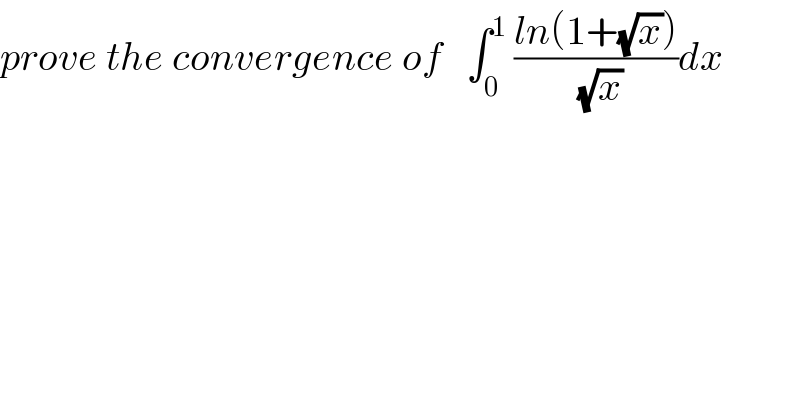 | ||
Commented by mathmax by abdo last updated on 06/Dec/19 | ||
![I=∫_0 ^1 ((ln(1+(√x)))/(√x))dx changement (√x)=t give x=t^2 ⇒ I =∫_0 ^1 ((ln(1+t))/t)(2t)dt =2 ∫_0 ^1 ln(1+t)dt =_(1+t=u) 2∫_1 ^2 ln(u)du =2[ulnu−u]_1 ^2 =2{2ln(2)−2+1} =4ln(2)−2](Q75057.png) | ||
Answered by mind is power last updated on 01/Dec/19 | ||
![u=(√x)⇒du=(1/(2(√x)))dx ∫_0 ^1 2ln(1+u)du=[2(u+1)ln(u+1)−2u]_0 ^1 =4ln(2)−2](Q74815.png) | ||
| ||