
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 74800 by mathmax by abdo last updated on 30/Nov/19
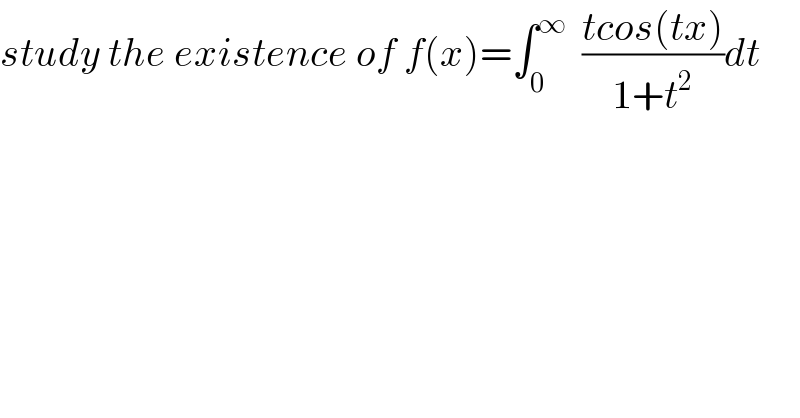
Answered by mind is power last updated on 30/Nov/19
![x=0 ∫_0 ^(+∞) (t/(1+t^2 ))dt divege for x#0 ipp [_0 ^(+∞) (t/(t^2 +1)).((sin(xt))/x)]−(1/x)∫_0 ^(+∞) sin(xt).(((1−t^2 ))/((1+t^2 )^2 ))dt =−(1/x)∫_0 ^(+∞) (((1−t^2 )sin(xt))/((1+t^2 )^2 ))dt exist cv abdolutly ≤(1/(∣x∣))∫_0 ^(+∞) ((∣(1−t^2 )∣)/((1+t^2 )^2 ))dt exist since at[+∞ (((t^2 −1))/((t^2 +1)^2 ))∼(1/t^2 ),wich is Reimann/integrabl at +∞ f(x) exist overR^∗](Q74812.png)
| ||
Question and Answers Forum | ||
Previous in Relation and Functions Next in Relation and Functions | ||
Question Number 74800 by mathmax by abdo last updated on 30/Nov/19 | ||
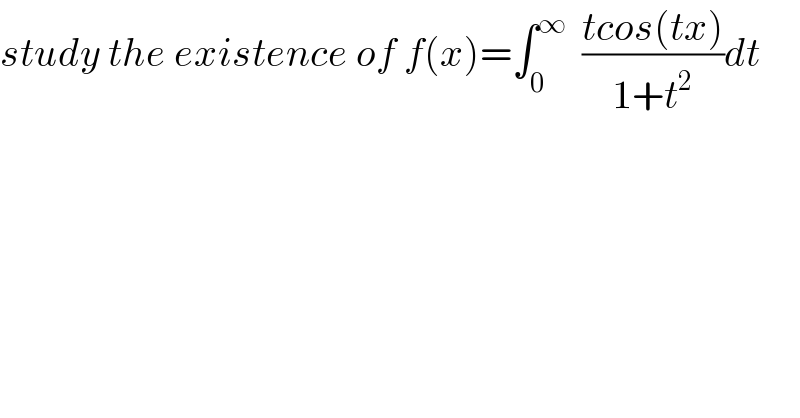 | ||
Answered by mind is power last updated on 30/Nov/19 | ||
![x=0 ∫_0 ^(+∞) (t/(1+t^2 ))dt divege for x#0 ipp [_0 ^(+∞) (t/(t^2 +1)).((sin(xt))/x)]−(1/x)∫_0 ^(+∞) sin(xt).(((1−t^2 ))/((1+t^2 )^2 ))dt =−(1/x)∫_0 ^(+∞) (((1−t^2 )sin(xt))/((1+t^2 )^2 ))dt exist cv abdolutly ≤(1/(∣x∣))∫_0 ^(+∞) ((∣(1−t^2 )∣)/((1+t^2 )^2 ))dt exist since at[+∞ (((t^2 −1))/((t^2 +1)^2 ))∼(1/t^2 ),wich is Reimann/integrabl at +∞ f(x) exist overR^∗](Q74812.png) | ||
| ||