
Question Number 7514 by Tawakalitu. last updated on 01/Sep/16

Answered by Yozzia last updated on 01/Sep/16
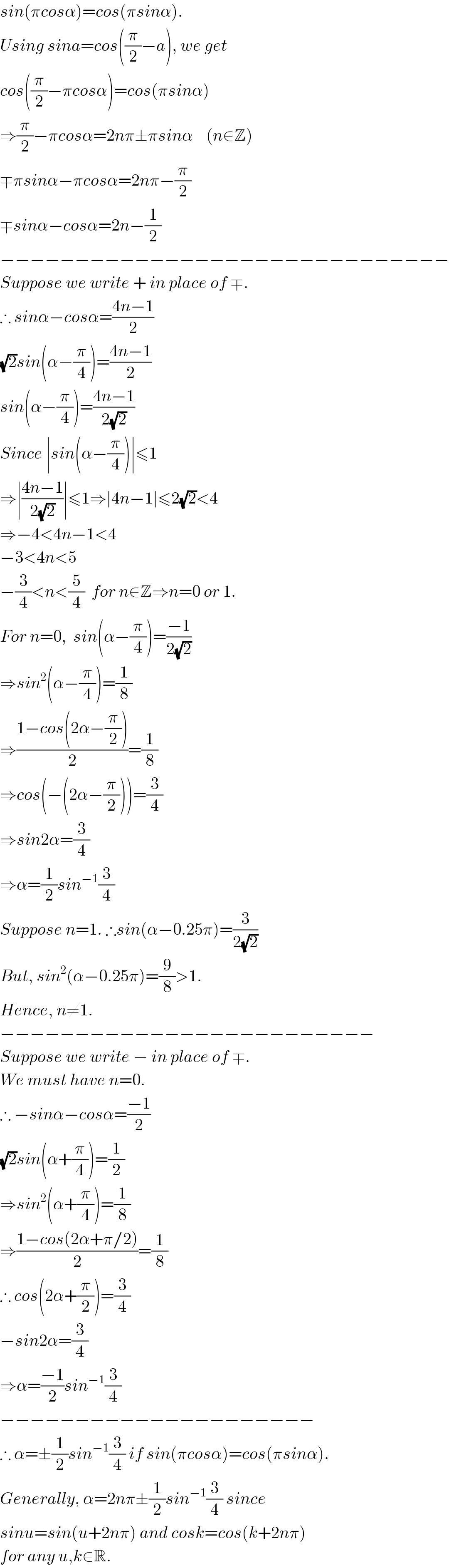
$${sin}\left(\pi{cos}\alpha\right)={cos}\left(\pi{sin}\alpha\right). \\ $$$${Using}\:{sina}={cos}\left(\frac{\pi}{\mathrm{2}}−{a}\right),\:{we}\:{get} \\ $$$${cos}\left(\frac{\pi}{\mathrm{2}}−\pi{cos}\alpha\right)={cos}\left(\pi{sin}\alpha\right) \\ $$$$\Rightarrow\frac{\pi}{\mathrm{2}}−\pi{cos}\alpha=\mathrm{2}{n}\pi\pm\pi{sin}\alpha\:\:\:\:\left({n}\in\mathbb{Z}\right) \\ $$$$\mp\pi{sin}\alpha−\pi{cos}\alpha=\mathrm{2}{n}\pi−\frac{\pi}{\mathrm{2}} \\ $$$$\mp{sin}\alpha−{cos}\alpha=\mathrm{2}{n}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${Suppose}\:{we}\:{write}\:+\:{in}\:{place}\:{of}\:\mp. \\ $$$$\therefore\:{sin}\alpha−{cos}\alpha=\frac{\mathrm{4}{n}−\mathrm{1}}{\mathrm{2}} \\ $$$$\sqrt{\mathrm{2}}{sin}\left(\alpha−\frac{\pi}{\mathrm{4}}\right)=\frac{\mathrm{4}{n}−\mathrm{1}}{\mathrm{2}} \\ $$$${sin}\left(\alpha−\frac{\pi}{\mathrm{4}}\right)=\frac{\mathrm{4}{n}−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$${Since}\:\mid{sin}\left(\alpha−\frac{\pi}{\mathrm{4}}\right)\mid\leqslant\mathrm{1} \\ $$$$\Rightarrow\mid\frac{\mathrm{4}{n}−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mid\leqslant\mathrm{1}\Rightarrow\mid\mathrm{4}{n}−\mathrm{1}\mid\leqslant\mathrm{2}\sqrt{\mathrm{2}}<\mathrm{4} \\ $$$$\Rightarrow−\mathrm{4}<\mathrm{4}{n}−\mathrm{1}<\mathrm{4} \\ $$$$−\mathrm{3}<\mathrm{4}{n}<\mathrm{5} \\ $$$$−\frac{\mathrm{3}}{\mathrm{4}}<{n}<\frac{\mathrm{5}}{\mathrm{4}}\:\:{for}\:{n}\in\mathbb{Z}\Rightarrow{n}=\mathrm{0}\:{or}\:\mathrm{1}. \\ $$$${For}\:{n}=\mathrm{0},\:\:{sin}\left(\alpha−\frac{\pi}{\mathrm{4}}\right)=\frac{−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow{sin}^{\mathrm{2}} \left(\alpha−\frac{\pi}{\mathrm{4}}\right)=\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\Rightarrow\frac{\mathrm{1}−{cos}\left(\mathrm{2}\alpha−\frac{\pi}{\mathrm{2}}\right)}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\Rightarrow{cos}\left(−\left(\mathrm{2}\alpha−\frac{\pi}{\mathrm{2}}\right)\right)=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow{sin}\mathrm{2}\alpha=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow\alpha=\frac{\mathrm{1}}{\mathrm{2}}{sin}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{4}} \\ $$$${Suppose}\:{n}=\mathrm{1}.\:\therefore{sin}\left(\alpha−\mathrm{0}.\mathrm{25}\pi\right)=\frac{\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$${But},\:{sin}^{\mathrm{2}} \left(\alpha−\mathrm{0}.\mathrm{25}\pi\right)=\frac{\mathrm{9}}{\mathrm{8}}>\mathrm{1}. \\ $$$${Hence},\:{n}\neq\mathrm{1}. \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${Suppose}\:{we}\:{write}\:−\:{in}\:{place}\:{of}\:\mp.\: \\ $$$${We}\:{must}\:{have}\:{n}=\mathrm{0}. \\ $$$$\therefore\:−{sin}\alpha−{cos}\alpha=\frac{−\mathrm{1}}{\mathrm{2}} \\ $$$$\sqrt{\mathrm{2}}{sin}\left(\alpha+\frac{\pi}{\mathrm{4}}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{sin}^{\mathrm{2}} \left(\alpha+\frac{\pi}{\mathrm{4}}\right)=\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\Rightarrow\frac{\mathrm{1}−{cos}\left(\mathrm{2}\alpha+\pi/\mathrm{2}\right)}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\therefore\:{cos}\left(\mathrm{2}\alpha+\frac{\pi}{\mathrm{2}}\right)=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$−{sin}\mathrm{2}\alpha=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow\alpha=\frac{−\mathrm{1}}{\mathrm{2}}{sin}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{4}} \\ $$$$−−−−−−−−−−−−−−−−−−−−− \\ $$$$\therefore\:\alpha=\pm\frac{\mathrm{1}}{\mathrm{2}}{sin}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{4}}\:{if}\:{sin}\left(\pi{cos}\alpha\right)={cos}\left(\pi{sin}\alpha\right). \\ $$$${Generally},\:\alpha=\mathrm{2}{n}\pi\pm\frac{\mathrm{1}}{\mathrm{2}}{sin}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{4}}\:{since} \\ $$$${sinu}={sin}\left({u}+\mathrm{2}{n}\pi\right)\:{and}\:{cosk}={cos}\left({k}+\mathrm{2}{n}\pi\right)\: \\ $$$${for}\:{any}\:{u},{k}\in\mathbb{R}. \\ $$
Commented by Tawakalitu. last updated on 01/Sep/16
$${Wow},\:{thanks}\:{so}\:{much}. \\ $$
