
Question and Answers Forum
Question Number 75230 by aliesam last updated on 08/Dec/19
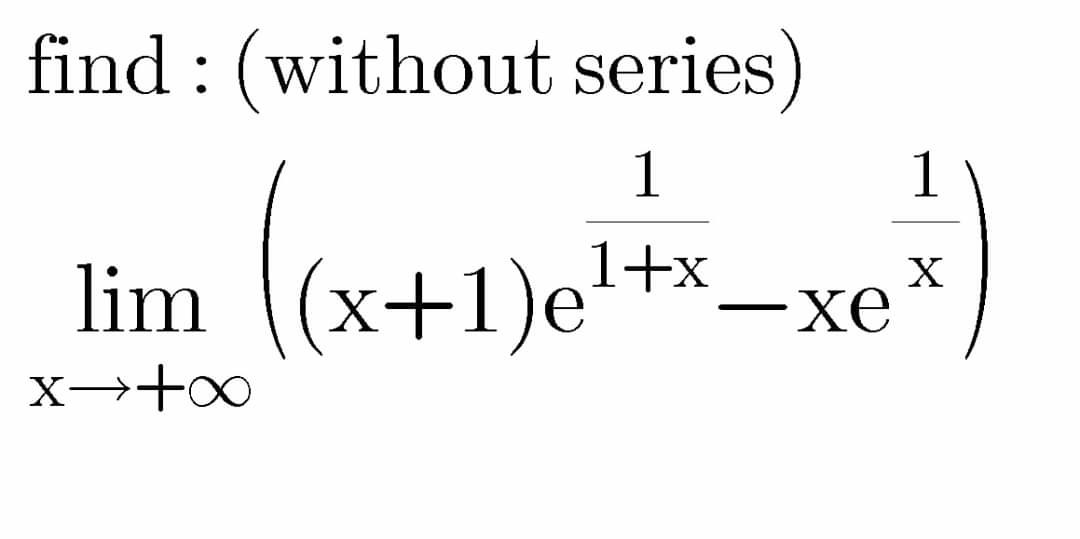
Commented by mathmax by abdo last updated on 08/Dec/19
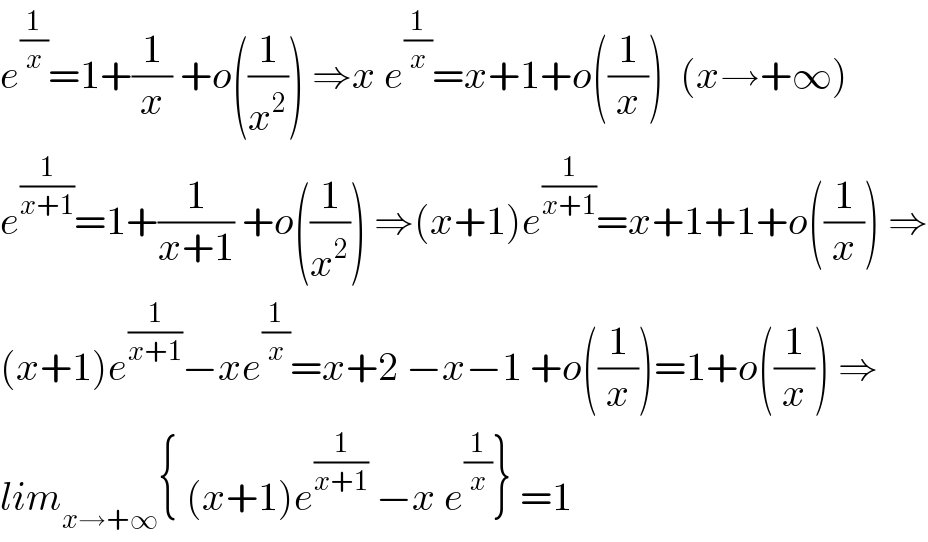
Answered by mind is power last updated on 08/Dec/19
![let f(z)=ze^(1/z) by mean value theorem ∃c∈]x,x+1[ f(x+1)−f(x)=f′(c) f′(c)=e^(1/c) −(e^(1/c) /c) since c>x⇒x→+∞,c→+∞ f′(c)→1 ⇒lim((x+1)e^(1/(x+1)) −xe^(1/x) )→1](Q75231.png)
Commented by aliesam last updated on 08/Dec/19

Commented by mind is power last updated on 08/Dec/19

