Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 75457 by Master last updated on 11/Dec/19

Commented by MJS last updated on 11/Dec/19

no exact solution possible try to approximate, there are 3 solutions, one real and two conjugated complex

$$\mathrm{no}\:\mathrm{exact}\:\mathrm{solution}\:\mathrm{possible} \\ $$$$\mathrm{try}\:\mathrm{to}\:\mathrm{approximate},\:\mathrm{there}\:\mathrm{are}\:\mathrm{3}\:\mathrm{solutions}, \\ $$$$\mathrm{one}\:\mathrm{real}\:\mathrm{and}\:\mathrm{two}\:\mathrm{conjugated}\:\mathrm{complex} \\ $$

Commented by behi83417@gmail.com last updated on 12/Dec/19

2x+1=t^2 ,x+1=s^2 ⇒x=s^2 −1,t^2 =2s^2 −1 ⇒(t/s^2 )+(s/t^2 )=5⇒t^3 +s^3 =5t^2 s^2 ⇒t^3 =s^2 (5t^2 −s)⇒t^6 =s^4 (25t^4 −10st^2 +s^2 ) ⇒(2s^2 −1)^3 =s^4 (25(2s^2 −1)^2 −10s(2s^2 −1)+s^2 ) ⇒8s^6 −12s^4 +6s^2 −1= =s^4 [100s^4 −100s^2 +25−20s^3 +10s+s^2 )= =100s^8 −20s^7 −99s^6 +10s^5 +25s^4 ⇒100s^8 −20s^7 −107s^6 +10s^5 +37s^4 −6s^2 +1=0 ⇒s=−0.661 ,0.753 ⇒[x=−0.563 ,−0.433]

$$\mathrm{2x}+\mathrm{1}=\mathrm{t}^{\mathrm{2}} ,\mathrm{x}+\mathrm{1}=\mathrm{s}^{\mathrm{2}} \Rightarrow\mathrm{x}=\mathrm{s}^{\mathrm{2}} −\mathrm{1},\mathrm{t}^{\mathrm{2}} =\mathrm{2s}^{\mathrm{2}} −\mathrm{1} \\ $$$$\Rightarrow\frac{\mathrm{t}}{\mathrm{s}^{\mathrm{2}} }+\frac{\mathrm{s}}{\mathrm{t}^{\mathrm{2}} }=\mathrm{5}\Rightarrow\mathrm{t}^{\mathrm{3}} +\mathrm{s}^{\mathrm{3}} =\mathrm{5t}^{\mathrm{2}} \mathrm{s}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{t}^{\mathrm{3}} =\mathrm{s}^{\mathrm{2}} \left(\mathrm{5t}^{\mathrm{2}} −\mathrm{s}\right)\Rightarrow\mathrm{t}^{\mathrm{6}} =\mathrm{s}^{\mathrm{4}} \left(\mathrm{25t}^{\mathrm{4}} −\mathrm{10st}^{\mathrm{2}} +\mathrm{s}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\left(\mathrm{2s}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} =\mathrm{s}^{\mathrm{4}} \left(\mathrm{25}\left(\mathrm{2s}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} −\mathrm{10s}\left(\mathrm{2s}^{\mathrm{2}} −\mathrm{1}\right)+\mathrm{s}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\mathrm{8s}^{\mathrm{6}} −\mathrm{12s}^{\mathrm{4}} +\mathrm{6s}^{\mathrm{2}} −\mathrm{1}= \\ $$$$=\mathrm{s}^{\mathrm{4}} \left[\mathrm{100s}^{\mathrm{4}} −\mathrm{100s}^{\mathrm{2}} +\mathrm{25}−\mathrm{20s}^{\mathrm{3}} +\mathrm{10s}+\mathrm{s}^{\mathrm{2}} \right)= \\ $$$$=\mathrm{100s}^{\mathrm{8}} −\mathrm{20s}^{\mathrm{7}} −\mathrm{99s}^{\mathrm{6}} +\mathrm{10s}^{\mathrm{5}} +\mathrm{25s}^{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{100s}^{\mathrm{8}} −\mathrm{20s}^{\mathrm{7}} −\mathrm{107s}^{\mathrm{6}} +\mathrm{10s}^{\mathrm{5}} +\mathrm{37s}^{\mathrm{4}} −\mathrm{6s}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\boldsymbol{\mathrm{s}}=−\mathrm{0}.\mathrm{661}\:\:,\mathrm{0}.\mathrm{753} \\ $$$$\Rightarrow\left[\mathrm{x}=−\mathrm{0}.\mathrm{563}\:\:,−\mathrm{0}.\mathrm{433}\right] \\ $$

Commented by MJS last updated on 12/Dec/19

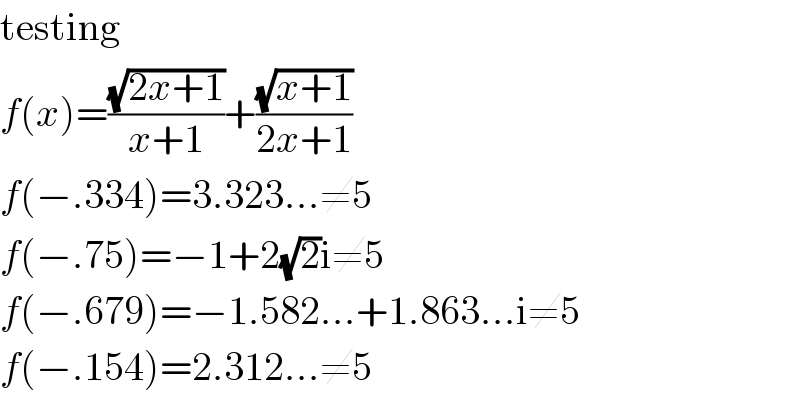
testing f(x)=((√(2x+1))/(x+1))+((√(x+1))/(2x+1)) f(−.334)=3.323...≠5 f(−.75)=−1+2(√2)i≠5 f(−.679)=−1.582...+1.863...i≠5 f(−.154)=2.312...≠5

$$\mathrm{testing} \\ $$$${f}\left({x}\right)=\frac{\sqrt{\mathrm{2}{x}+\mathrm{1}}}{{x}+\mathrm{1}}+\frac{\sqrt{{x}+\mathrm{1}}}{\mathrm{2}{x}+\mathrm{1}} \\ $$$${f}\left(−.\mathrm{334}\right)=\mathrm{3}.\mathrm{323}...\neq\mathrm{5} \\ $$$${f}\left(−.\mathrm{75}\right)=−\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}\mathrm{i}\neq\mathrm{5} \\ $$$${f}\left(−.\mathrm{679}\right)=−\mathrm{1}.\mathrm{582}...+\mathrm{1}.\mathrm{863}...\mathrm{i}\neq\mathrm{5} \\ $$$${f}\left(−.\mathrm{154}\right)=\mathrm{2}.\mathrm{312}...\neq\mathrm{5} \\ $$

Commented by MJS last updated on 12/Dec/19

error in line 3 from end it must be 37s^4 instead of 31s^4 ⇒ you get the same solutions as me

$$\mathrm{error}\:\mathrm{in}\:\mathrm{line}\:\mathrm{3}\:\mathrm{from}\:\mathrm{end} \\ $$$$\mathrm{it}\:\mathrm{must}\:\mathrm{be}\:\mathrm{37}{s}^{\mathrm{4}} \:\mathrm{instead}\:\mathrm{of}\:\mathrm{31}{s}^{\mathrm{4}} \\ $$$$\Rightarrow \\ $$$$\mathrm{you}\:\mathrm{get}\:\mathrm{the}\:\mathrm{same}\:\mathrm{solutions}\:\mathrm{as}\:\mathrm{me} \\ $$

Commented by MJS last updated on 12/Dec/19

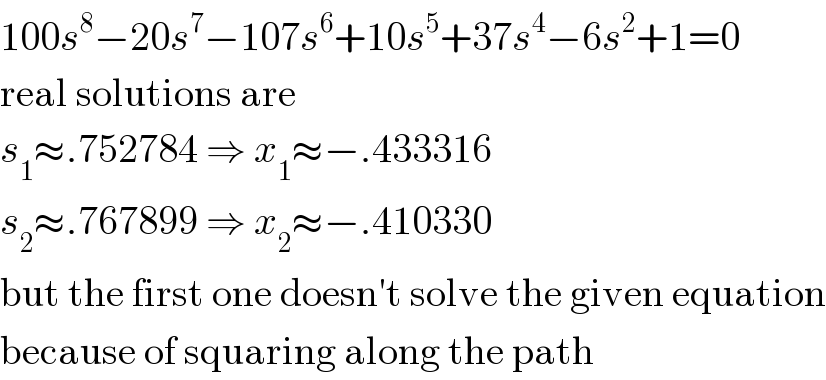
100s^8 −20s^7 −107s^6 +10s^5 +37s^4 −6s^2 +1=0 real solutions are s_1 ≈.752784 ⇒ x_1 ≈−.433316 s_2 ≈.767899 ⇒ x_2 ≈−.410330 but the first one doesn′t solve the given equation because of squaring along the path

$$\mathrm{100}{s}^{\mathrm{8}} −\mathrm{20}{s}^{\mathrm{7}} −\mathrm{107}{s}^{\mathrm{6}} +\mathrm{10}{s}^{\mathrm{5}} +\mathrm{37}{s}^{\mathrm{4}} −\mathrm{6}{s}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{real}\:\mathrm{solutions}\:\mathrm{are} \\ $$$${s}_{\mathrm{1}} \approx.\mathrm{752784}\:\Rightarrow\:{x}_{\mathrm{1}} \approx−.\mathrm{433316} \\ $$$${s}_{\mathrm{2}} \approx.\mathrm{767899}\:\Rightarrow\:{x}_{\mathrm{2}} \approx−.\mathrm{410330} \\ $$$$\mathrm{but}\:\mathrm{the}\:\mathrm{first}\:\mathrm{one}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{given}\:\mathrm{equation} \\ $$$$\mathrm{because}\:\mathrm{of}\:\mathrm{squaring}\:\mathrm{along}\:\mathrm{the}\:\mathrm{path} \\ $$

Answered by peter frank last updated on 11/Dec/19

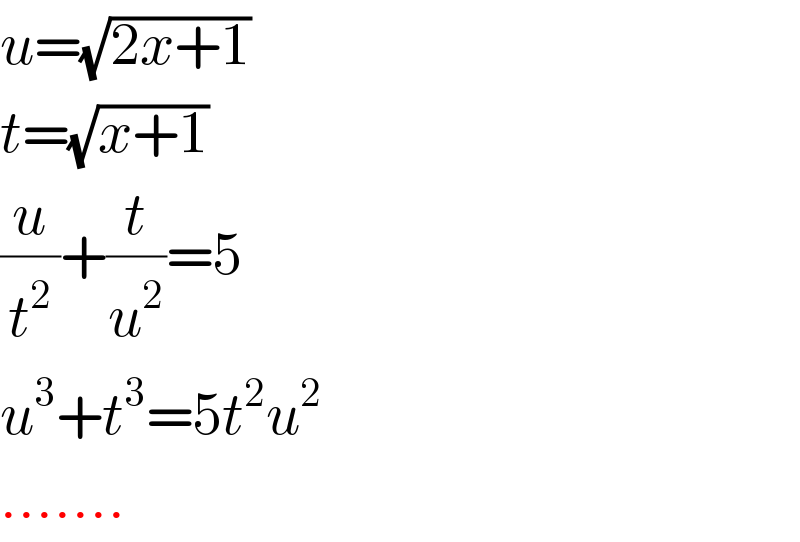
u=(√(2x+1)) t=(√(x+1)) (u/t^2 )+(t/u^2 )=5 u^3 +t^3 =5t^2 u^2 .......

$${u}=\sqrt{\mathrm{2}{x}+\mathrm{1}} \\ $$$${t}=\sqrt{{x}+\mathrm{1}} \\ $$$$\frac{{u}}{{t}^{\mathrm{2}} }+\frac{{t}}{{u}^{\mathrm{2}} }=\mathrm{5} \\ $$$${u}^{\mathrm{3}} +{t}^{\mathrm{3}} =\mathrm{5}{t}^{\mathrm{2}} {u}^{\mathrm{2}} \\ $$$$....... \\ $$

Answered by MJS last updated on 12/Dec/19

squaring, transforming, squaring again leads to x^8 +((291)/(50))x^7 +((146649)/(10000))x^6 +((52119)/(2500))x^5 +((91249)/(5000))x^4 +((50277)/(5000))x^3 +((34009)/(10000))x^2 +((129)/(200))x+((21)/(400))=0 but we have to test all solutions because squaring leads to false solutions the approximated roots are: x_1 ≈−.433316 wrong x_2 ≈−.410330 right x_(3, 4) ≈−.973872±.209039i wrong x_(5, 6) ≈−.950789±.181535i right x_(7, 8) ≈−.563516±.00951046i wrong ⇒ the solutions are x≈−.410330∨x≈−.950789±.181535i

$$\mathrm{squaring},\:\mathrm{transforming},\:\mathrm{squaring}\:\mathrm{again}\:\mathrm{leads}\:\mathrm{to} \\ $$$${x}^{\mathrm{8}} +\frac{\mathrm{291}}{\mathrm{50}}{x}^{\mathrm{7}} +\frac{\mathrm{146649}}{\mathrm{10000}}{x}^{\mathrm{6}} +\frac{\mathrm{52119}}{\mathrm{2500}}{x}^{\mathrm{5}} +\frac{\mathrm{91249}}{\mathrm{5000}}{x}^{\mathrm{4}} +\frac{\mathrm{50277}}{\mathrm{5000}}{x}^{\mathrm{3}} +\frac{\mathrm{34009}}{\mathrm{10000}}{x}^{\mathrm{2}} +\frac{\mathrm{129}}{\mathrm{200}}{x}+\frac{\mathrm{21}}{\mathrm{400}}=\mathrm{0} \\ $$$$\mathrm{but}\:\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{test}\:\mathrm{all}\:\mathrm{solutions}\:\mathrm{because} \\ $$$$\mathrm{squaring}\:\mathrm{leads}\:\mathrm{to}\:\mathrm{false}\:\mathrm{solutions} \\ $$$$\mathrm{the}\:\mathrm{approximated}\:\mathrm{roots}\:\mathrm{are}: \\ $$$${x}_{\mathrm{1}} \approx−.\mathrm{433316}\:\mathrm{wrong} \\ $$$${x}_{\mathrm{2}} \approx−.\mathrm{410330}\:\mathrm{right} \\ $$$${x}_{\mathrm{3},\:\mathrm{4}} \approx−.\mathrm{973872}\pm.\mathrm{209039i}\:\mathrm{wrong} \\ $$$${x}_{\mathrm{5},\:\mathrm{6}} \approx−.\mathrm{950789}\pm.\mathrm{181535i}\:\mathrm{right} \\ $$$${x}_{\mathrm{7},\:\mathrm{8}} \approx−.\mathrm{563516}\pm.\mathrm{00951046i}\:\mathrm{wrong} \\ $$$$\Rightarrow \\ $$$$\mathrm{the}\:\mathrm{solutions}\:\mathrm{are} \\ $$$${x}\approx−.\mathrm{410330}\vee{x}\approx−.\mathrm{950789}\pm.\mathrm{181535i} \\ $$

Commented by behi83417@gmail.com last updated on 12/Dec/19

thank you very much sir proph: MJS. I fixed the error,but answers not much with yours.

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{sir}\:\mathrm{proph}:\:\mathrm{MJS}. \\ $$$$\mathrm{I}\:\mathrm{fixed}\:\mathrm{the}\:\mathrm{error},\mathrm{but}\:\mathrm{answers}\:\mathrm{not}\:\mathrm{much} \\ $$$$\mathrm{with}\:\mathrm{yours}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com