
Question and Answers Forum
Question Number 75484 by vishalbhardwaj last updated on 11/Dec/19
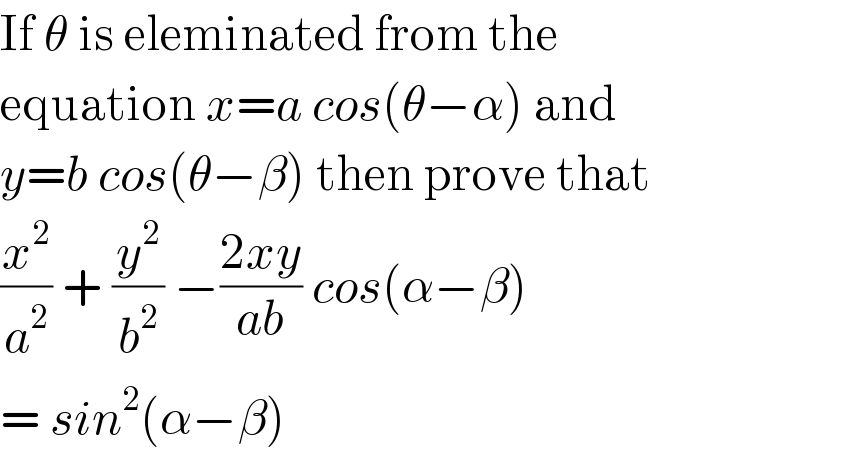
Answered by MJS last updated on 12/Dec/19
![x=acos (θ−α) ⇒ θ=α−arccos (x/a) y=bcos (α−β−arccos (x/a)) [cos (u+v) =cos u cos v −sin u sin v] [sin (u+v) =cos u sin v −sin u cos v] y=(b/a)xcos (α−β)±(b/a)(√(a^2 −x^2 ))sin (α−β) (x^2 /a^2 )+(y^2 /b^2 )−((2xy)/(ab))cos (α−β) =sin^2 (α−β) ⇒ y=(b/a)xcos (α−β)±(b/a)(√(a^2 −x^2 ))sin (α−β) same as above ⇒ proved](Q75491.png)
| ||
Question and Answers Forum | ||
Question Number 75484 by vishalbhardwaj last updated on 11/Dec/19 | ||
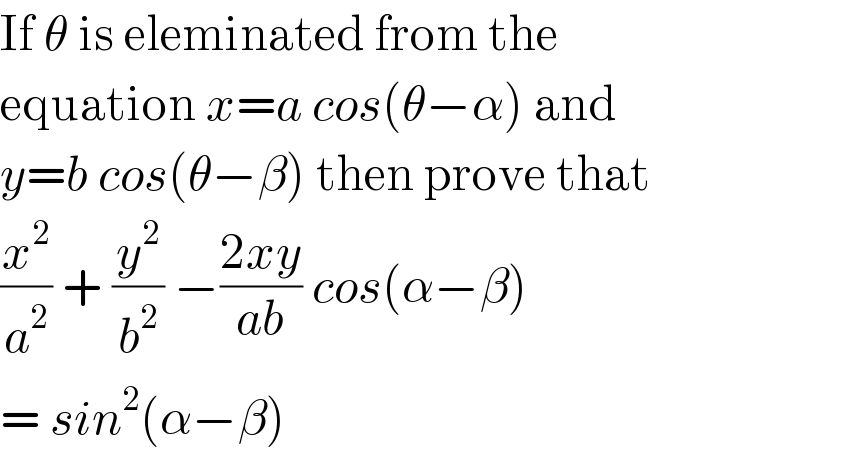 | ||
Answered by MJS last updated on 12/Dec/19 | ||
![x=acos (θ−α) ⇒ θ=α−arccos (x/a) y=bcos (α−β−arccos (x/a)) [cos (u+v) =cos u cos v −sin u sin v] [sin (u+v) =cos u sin v −sin u cos v] y=(b/a)xcos (α−β)±(b/a)(√(a^2 −x^2 ))sin (α−β) (x^2 /a^2 )+(y^2 /b^2 )−((2xy)/(ab))cos (α−β) =sin^2 (α−β) ⇒ y=(b/a)xcos (α−β)±(b/a)(√(a^2 −x^2 ))sin (α−β) same as above ⇒ proved](Q75491.png) | ||
| ||