
Question and Answers Forum
Question Number 75502 by mathocean1 last updated on 12/Dec/19
![Solve it in ]−π;π] sin(2x)=cos(x)](Q75502.png)
Commented by mathmax by abdo last updated on 12/Dec/19
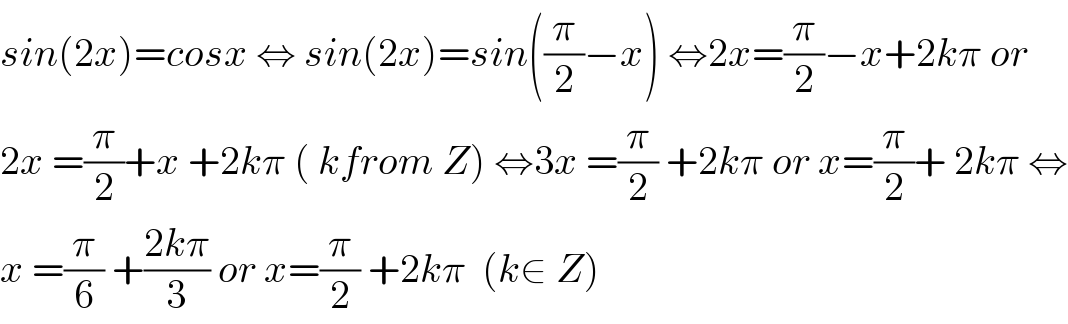
Commented by mathmax by abdo last updated on 12/Dec/19

| ||
Question and Answers Forum | ||
Question Number 75502 by mathocean1 last updated on 12/Dec/19 | ||
![Solve it in ]−π;π] sin(2x)=cos(x)](Q75502.png) | ||
Commented by mathmax by abdo last updated on 12/Dec/19 | ||
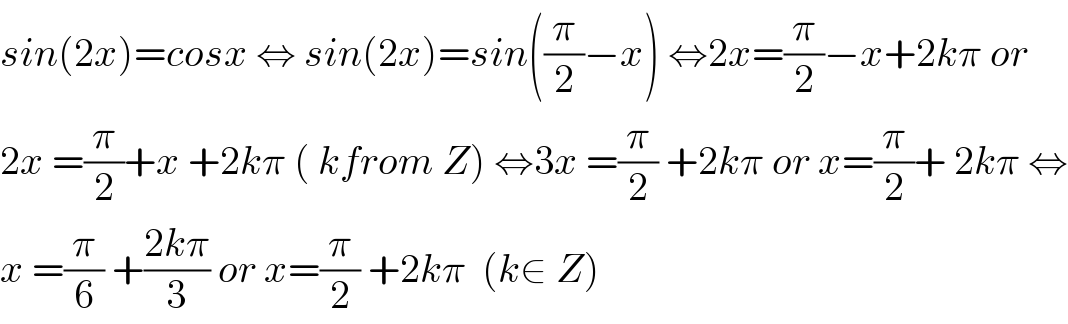 | ||
Commented by mathmax by abdo last updated on 12/Dec/19 | ||
 | ||