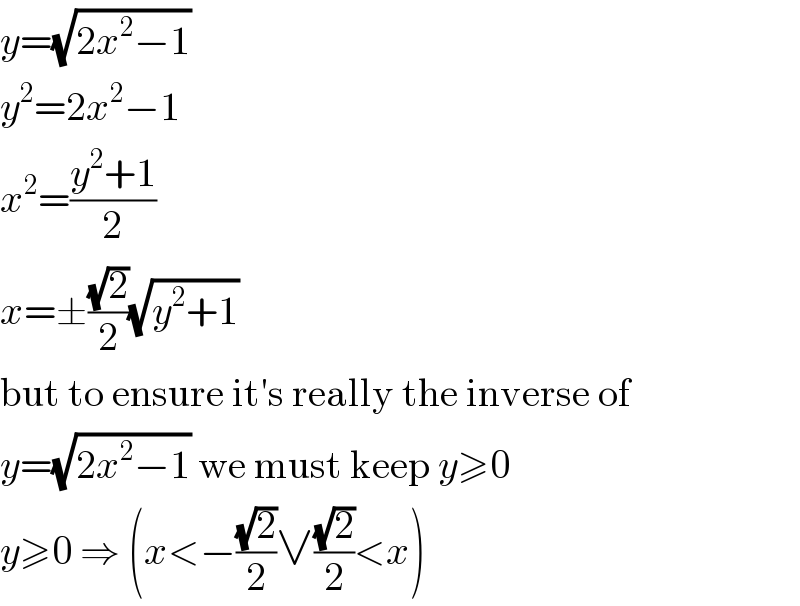Question and Answers Forum
Question Number 75527 by liki last updated on 12/Dec/19

Commented by liki last updated on 12/Dec/19

Answered by MJS last updated on 12/Dec/19
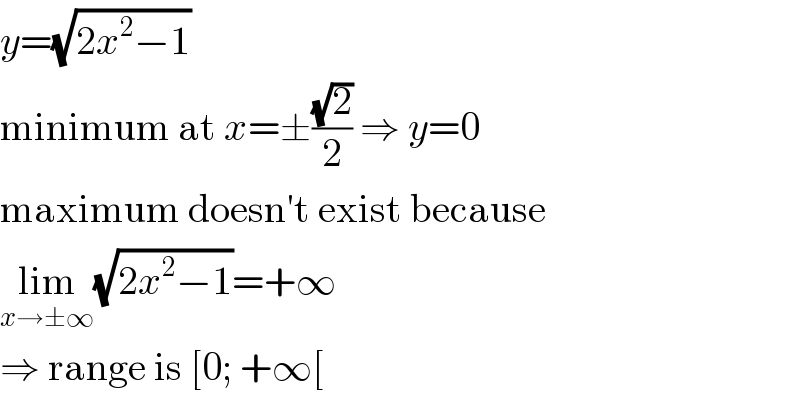
Commented by liki last updated on 12/Dec/19
Commented by liki last updated on 12/Dec/19
Commented by MJS last updated on 12/Dec/19
![defined for x∈R\]−((√2)/2); ((√2)/2)[](Q75533.png)
Commented by liki last updated on 12/Dec/19
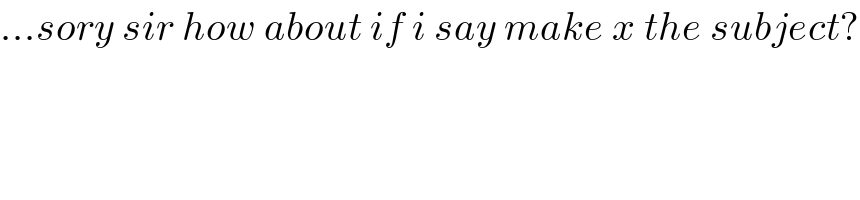
Commented by MJS last updated on 12/Dec/19