
Question and Answers Forum
Question Number 75547 by TawaTawa last updated on 12/Dec/19
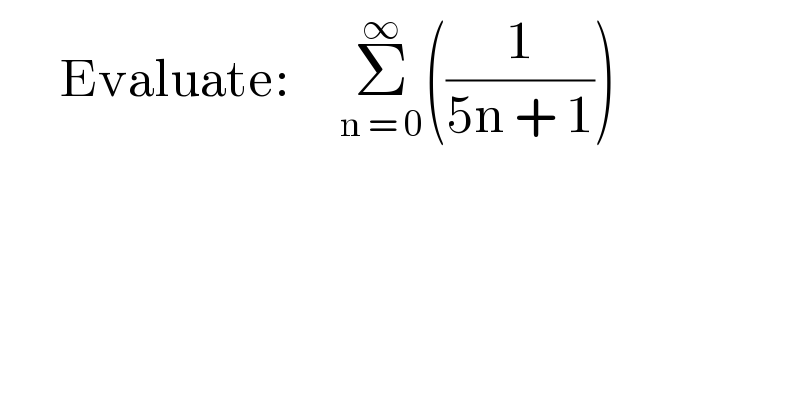
Commented by mind is power last updated on 13/Dec/19
![mor generaly let S=Σ_(k≥0) (((−1)^k )/(ak+b)) withe (a,b)∈N^(∗2) withe gcd(a,b)=1 S=(1/b).Σ(((−1)^k )/(1+(a/b)k)) let f(x)=(1/(1+x^(a/b) )) ∣x∣<1⇒f(x)=Σ_(k≥0) (−1)^k .x^((ak)/b) let ε>0⇒ since we have unifirm cv we switch ÷ ∫_0 ^(1−ε) f(x)dx=Σ_(k≥0) (−1)^k ∫_0 ^(1−ε) x^((ak)/b) dx S=Σ_(k≥0) (−1)^k .(1/(1+((ak)/b)))(1−ε)^(((ak)/b)+1) we tack ε→0 justify by the fact ∀ε>0 S= Σ_(k≥0) (((−1)^k )/(1+((ak)/b)))(1−ε)^(((ak)/b)+1) Converge uniformily in compact [0,1−ε] ∫_0 ^1 (dx/(1+x^(a/b) ))=S,(a/b)≠1 since gcd(a,b)=1 x=tg^(2(b/a)) u ⇒dx=((2b)/a)(1+tg^2 (u))tg^((2b−a)/a) (u)du S=((2b)/a).∫_0 ^(π/4) tg^((2b−a)/a) (u)du S=((2b)/a)∫_0 ^(π/4) sin^(((2b)/a)−1) (u).cos^(((−2b)/a)+2−1) (u)du withe B^∼ (x,y,s)=2∫_0 ^s cos^(2x−1) (t).sin^(2y−1) (t)dt bS=(b/a)B^∼ ((b/a),1−(b/a),(π/4)) ⇒Σ_(k≥0) (((−1)^k )/(ak+b))=((B^∼ ((b/a),1−(b/a),(π/4)))/a) ,∀(a,b)∈N^(∗2) withe gcd(a,b)=1 and (a,b)≠(1,1)](Q75587.png)
Commented by mathmax by abdo last updated on 12/Dec/19
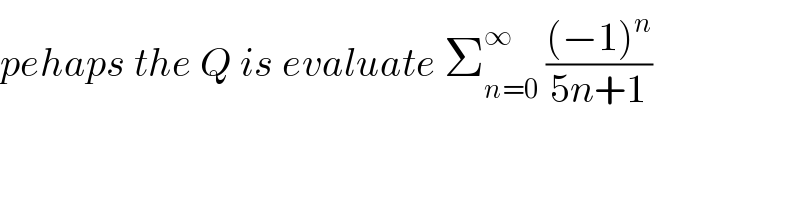
Commented by TawaTawa last updated on 12/Dec/19

Commented by TawaTawa last updated on 13/Dec/19
Commented by mind is power last updated on 13/Dec/19

Answered by mind is power last updated on 12/Dec/19

Answered by mind is power last updated on 12/Dec/19
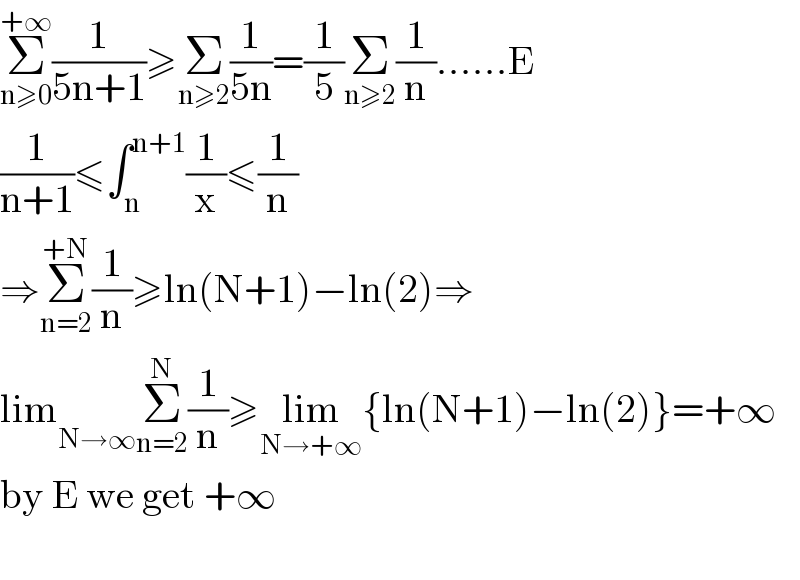
Commented by TawaTawa last updated on 12/Dec/19

