Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 75830 by Master last updated on 18/Dec/19

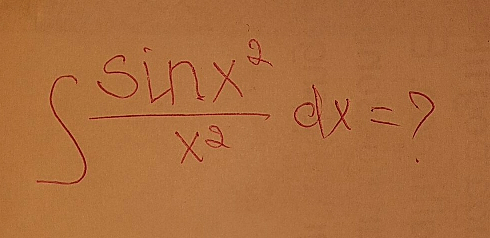
Commented by Master last updated on 18/Dec/19

$$\mathrm{sir}\mathrm{mind}\mathrm{is}\mathrm{power},\mathrm{sir}\mathrm{mathmax}\mathrm{plz}$$

Commented by turbo msup by abdo last updated on 18/Dec/19

$$doyoumean{\left(sinx\right)}^{2}orsin\left(x^2\right)?$$

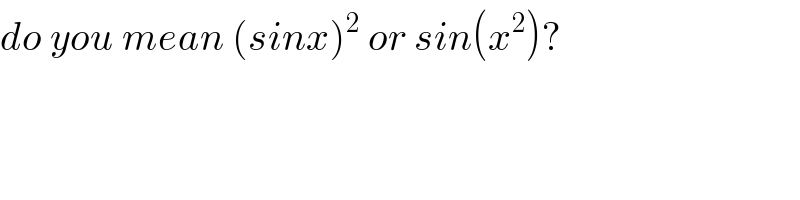
Commented by Master last updated on 18/Dec/19

$$\sin \left({\mathrm{x}}^2\right)$$

Commented by mathmax by abdo last updated on 19/Dec/19

$$atformofseriewehavesin\left(x^2\right)=\sum _{n=0}^{\mathrm{\infty }}\frac{{(-1)}^n{\left(x^2\right)}^{2n+1}}{(2n+1)!}$$$$=\sum _{n=0}^{\mathrm{\infty }}\frac{{(-1)}^n{x}^{4n+2}}{(2n+1)!}\Rightarrow \frac{sin\left(x^2\right)}{x^2}=\sum _{n=0}^{\mathrm{\infty }}\frac{{(-1)}^n}{(2n+1)!}{x}^{4n}\Rightarrow$$$$\int \frac{sin\left(x^2\right)}{x^2}dx=\sum _{n=0}^{\mathrm{\infty }}\frac{{(-1)}^n}{(2n+1)(4n+1)}{x}^{4n+1}+C$$

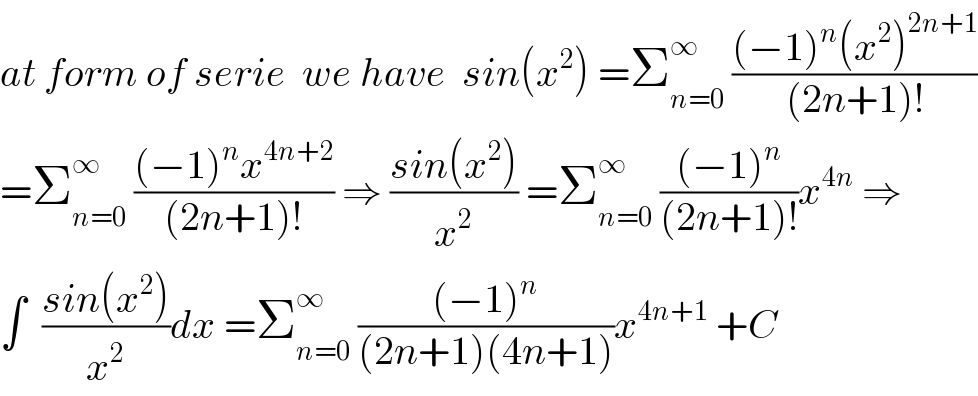
Commented by abdomathmax last updated on 19/Dec/19

$$letf\left(x\right)={\int }_0^x\frac{sin\left(t^2\right)}{t^2}dt\Rightarrow$$$$f\left(x\right)={[-\frac{sin\left(t^2\right)}{t}]}_0^x-{\int }_0^x(-\frac{1}{t})(2tcos\left(t^2\right)dt$$$$=-\frac{sin\left(x^2\right)}{x}+2{\int }_0^{x}cos\left(t^2\right)dt$$$${\int }_0^{x}cos\left(t^2\right)dt=Re\left({\int }_0^x{e}^{-{it}^2}dt\right)andchangement$$$${it}^2=ugive{t}^2=-iu\Rightarrow t={(-iu)}^{\frac{1}{2}}\Rightarrow$$$$dt={(-i)}^{\frac{1}{2}}\frac{1}{2}{u}^{-\frac{1}{2}}=\frac{1}{2}{e}^{-\frac{i\pi }{4}}{u}^{-\frac{1}{2}}\Rightarrow$$$${\int }_0^x{e}^{-{it}^2}dt=\frac{1}{2}{e}^{-\frac{i\pi }{4}}{\int }_0^{{ix}^2}{e}^{-u}{u}^{-\frac{1}{2}}du$$$$...becontinued...$$

Answered by mr W last updated on 18/Dec/19

$$=\int \sin x^{2}d(-\frac{1}{x})$$$$=-\frac{\sin x^2}{x}+2\int \cos x^{2}dx$$$$=-\frac{\sin x^2}{x}+\sqrt{2\pi }\int \cos \left[\frac{\pi }{2}{\left(\frac{\sqrt{2}x}{\sqrt{\pi }}\right)}^2\right]d\left(\frac{\sqrt{2}x}{\sqrt{\pi }}\right)$$$$=-\frac{\sin x^2}{x}+\sqrt{2\pi }C\left(\frac{\sqrt{2}x}{\sqrt{\pi }}\right)+C$$$$withFresnelintegral:$$$$S\left(x\right)={\int }_0^x\sin \left(\frac{\pi t^2}{2}\right)dt$$$$C\left(x\right)={\int }_0^x\cos \left(\frac{\pi t^2}{2}\right)dt$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com