
Question and Answers Forum
Question Number 75933 by Rio Michael last updated on 21/Dec/19
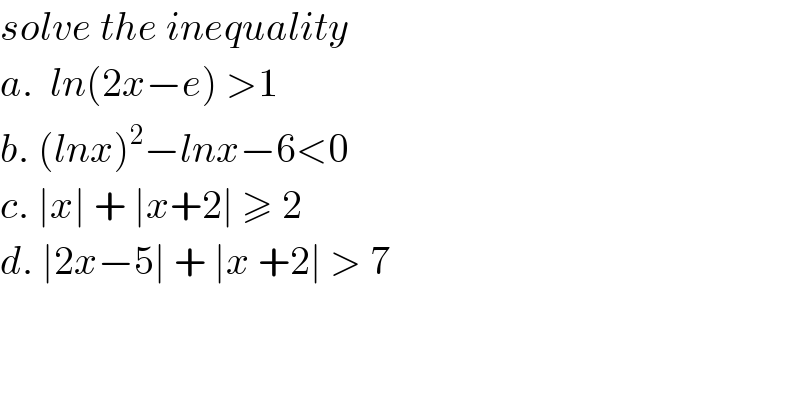
Commented bymathmax by abdo last updated on 21/Dec/19
![for x>(e/2) we have ln(2x−e)>1 ⇒ln(2x−e)>ln(e) ⇒ 2x−e>e ⇒2x>2e ⇒x>e ⇒S=]e,+∞[ b) let lnx=t with x>0 (e) ⇔ t^2 −t−6<0 Δ=1−4(−6) =25 ⇒t_1 =((1+5)/2) =3 and t_2 =((1−5)/2) =−2 t^2 −t−6<0 ⇔ −2<t<3 ⇒−2<lnx<3 ⇒e^(−2) <x<e^3 c) ∣x∣ +∣x+2∣≥2 ⇔ ∣x∣+∣x+2∣−2≥0 let A(x)=∣x∣+∣x+2∣−2 x −2 0 +∞ ∣x∣ −x −x x ∣x+2∣ −x−2 x+2 x+2 A(x) −2x−4 0 2x case 1 x≤−2 (in) ⇔ /−2x−4 ≥0 ⇔ −2x≥4 ⇔ 2x≤−4 ⇔x≤−2 ⇒S_1 =]−∞,−2] case 2 −2≤x≤0 (in) ⇔ 0≥0 (true)⇒s_2 =[−2,0] case 3 x≥0 (in) ⇔ 2x≥0 ⇒x ≥0 ⇒S_3 =[0,+∞[ ⇒ S =∪ Si=R .](Q75995.png)
Commented byRio Michael last updated on 21/Dec/19

| ||
Question and Answers Forum | ||
Question Number 75933 by Rio Michael last updated on 21/Dec/19 | ||
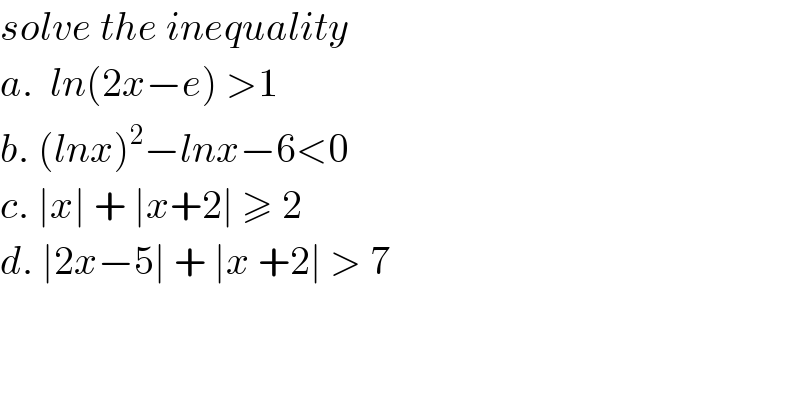 | ||
Commented bymathmax by abdo last updated on 21/Dec/19 | ||
![for x>(e/2) we have ln(2x−e)>1 ⇒ln(2x−e)>ln(e) ⇒ 2x−e>e ⇒2x>2e ⇒x>e ⇒S=]e,+∞[ b) let lnx=t with x>0 (e) ⇔ t^2 −t−6<0 Δ=1−4(−6) =25 ⇒t_1 =((1+5)/2) =3 and t_2 =((1−5)/2) =−2 t^2 −t−6<0 ⇔ −2<t<3 ⇒−2<lnx<3 ⇒e^(−2) <x<e^3 c) ∣x∣ +∣x+2∣≥2 ⇔ ∣x∣+∣x+2∣−2≥0 let A(x)=∣x∣+∣x+2∣−2 x −2 0 +∞ ∣x∣ −x −x x ∣x+2∣ −x−2 x+2 x+2 A(x) −2x−4 0 2x case 1 x≤−2 (in) ⇔ /−2x−4 ≥0 ⇔ −2x≥4 ⇔ 2x≤−4 ⇔x≤−2 ⇒S_1 =]−∞,−2] case 2 −2≤x≤0 (in) ⇔ 0≥0 (true)⇒s_2 =[−2,0] case 3 x≥0 (in) ⇔ 2x≥0 ⇒x ≥0 ⇒S_3 =[0,+∞[ ⇒ S =∪ Si=R .](Q75995.png) | ||
Commented byRio Michael last updated on 21/Dec/19 | ||
 | ||