Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 75960 by Tony Lin last updated on 21/Dec/19

$$provethat{\int }_0^{\frac{\pi }{2}}ln\left(sinx\right)dx=-\frac{\pi }{2}ln2$$

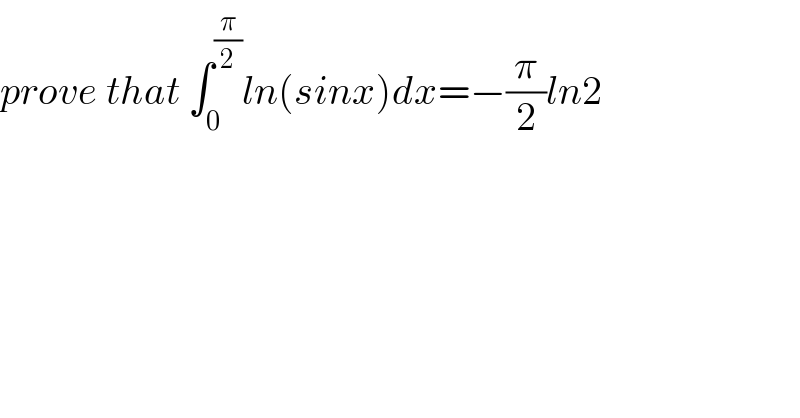
Commented by Kunal12588 last updated on 21/Dec/19

$$nowsolve{\int }_0^{\frac{\pi }{2}}ln\left(cosx\right)dx$$

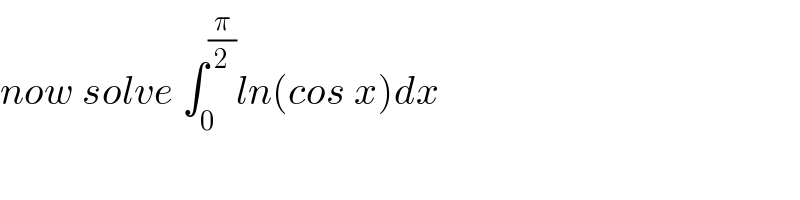
Commented by Tony Lin last updated on 23/Dec/19

$${\int }_0^{\frac{\pi }{2}}ln\left(sinx\right)dx$$$$let\theta =\frac{\pi }{2}-x,d\theta =-dx$$$$-{\int }_{\frac{\pi }{2}}^{0}ln\left[sin(\frac{\pi }{2}-x)\right]d\theta$$$$={\int }_0^{\frac{\pi }{2}}ln\left(cosx\right)dx$$

Answered by Kunal12588 last updated on 21/Dec/19

$$I={\int }_0^{\frac{\pi }{2}}ln\left(sinx\right)dx$$$$\Rightarrow I={\int }_0^{\frac{\pi }{2}}ln\left(cosx\right)dx$$$$2I={\int }_0^{\frac{\pi }{2}}ln\left(sinxcosx\right)dx$$$$\Rightarrow 2I={\int }_0^{\frac{\pi }{2}}[ln\left(sin2x\right)-ln\left(2\right)]dx$$$$\Rightarrow 2I={\int }_0^{\frac{\pi }{2}}ln\left(sin2x\right)dx-{\left[xln2\right]}_0^{\frac{\pi }{2}}$$$$lett=2x\Rightarrow dx=\frac{1}{2}dt$$$$x\to 0\Rightarrow t\to 0$$$$x\to \frac{\pi }{2}\Rightarrow t\to \pi$$$$2I=\frac{1}{2}{\int }_0^{\pi }ln\left(sint\right)dt-\frac{\pi }{2}ln2$$$$\Rightarrow 2I=\frac{1}{2}\times 2{\int }_0^{\frac{\pi }{2}}ln\left(sinx\right)dx-\frac{\pi }{2}ln2$$$$\Rightarrow 2I=I-\frac{\pi }{2}ln2$$$$\Rightarrow I=-\frac{\pi }{2}ln2proved$$

Commented by Tony Lin last updated on 23/Dec/19

$$thankssir$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com