
Question Number 7598 by Rohit last updated on 05/Sep/16
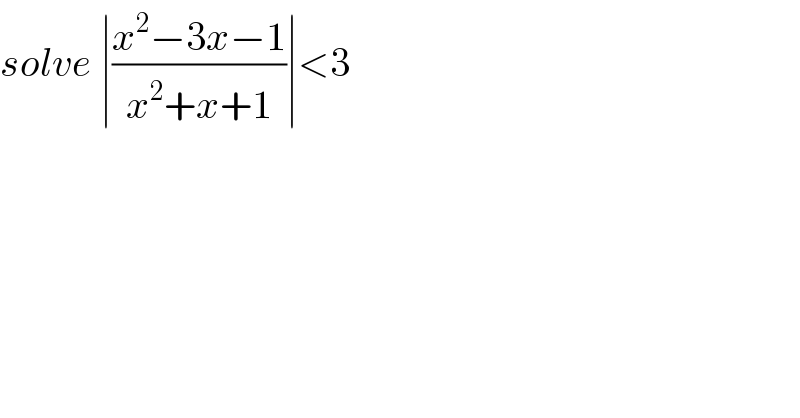
$${solve}\:\mid\frac{{x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\mid<\mathrm{3} \\ $$
Answered by Rasheed Soomro last updated on 06/Sep/16
![∣((x^2 −3x−1)/(x^2 +x+1))∣<3 ±((x^2 −3x−1)/(x^2 +x+1))<3 ((x^2 −3x−1)/(x^2 +x+1))<3 ∣ −((x^2 −3x−1)/(x^2 +x+1))<3 ((x^2 −3x−1)/(x^2 +x+1))<3 ∣ ((x^2 −3x−1)/(x^2 +x+1))>−3 x^2 +x+1>0 [See the reason in the comment by Sandy below or see the explanation for this in the answer by Yozzia.] x^2 −3x−1<3x^2 +3x+3 ∣ x^2 −3x−1>−3x^2 −3x−3 2x^2 +6x+4>0 ∣ 4x^2 +2>0 x^2 +3x+2>0 ∣ 2x^2 +1>0 (x+2)(x+1)>0 ∣ x^2 >−(1/2)⇒x^2 >0⇒ x>0 ∨ x<0 (x+2>0 ∧ x+1>0 ) or (x+2<0 ∧ x+1<0 ) x>−2 ∧ x>−1 or x<−2 ∧ x<−1 x>−1 or x<−2](Q7603.png)
$$\mid\frac{{x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\mid<\mathrm{3} \\ $$ $$\pm\frac{{x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}<\mathrm{3} \\ $$ $$\frac{{x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}<\mathrm{3}\:\:\:\mid\:\:\:−\frac{{x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}<\mathrm{3} \\ $$ $$\frac{{x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}<\mathrm{3}\:\:\:\mid\:\:\:\frac{{x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}>−\mathrm{3} \\ $$ $$ \\ $$ $$\:{x}^{\mathrm{2}} +{x}+\mathrm{1}>\mathrm{0}\:\:\left[{See}\:{the}\:{reason}\:{in}\:{the}\:{comment}\:{by}\:{Sandy}\:{below}\right. \\ $$ $$\left.{or}\:{see}\:{the}\:{explanation}\:{for}\:{this}\:{in}\:{the}\:{answer}\:{by}\:{Yozzia}.\right] \\ $$ $${x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{1}<\mathrm{3}{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{3}\:\:\mid\:\:{x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{1}>−\mathrm{3}{x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{3} \\ $$ $$\mathrm{2}{x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{4}>\mathrm{0}\:\:\:\:\:\:\:\:\mid\:\:\:\:\:\mathrm{4}{x}^{\mathrm{2}} +\mathrm{2}>\mathrm{0} \\ $$ $${x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{2}>\mathrm{0}\:\:\:\:\:\:\:\:\:\mid\:\:\:\:\:\:\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}>\mathrm{0} \\ $$ $$\left({x}+\mathrm{2}\right)\left({x}+\mathrm{1}\right)>\mathrm{0}\:\:\:\mid\:\:\:\:\:\:{x}^{\mathrm{2}} >−\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow{x}^{\mathrm{2}} >\mathrm{0}\Rightarrow\:{x}>\mathrm{0}\:\vee\:{x}<\mathrm{0} \\ $$ $$\left({x}+\mathrm{2}>\mathrm{0}\:\wedge\:{x}+\mathrm{1}>\mathrm{0}\:\right)\:{or}\:\left({x}+\mathrm{2}<\mathrm{0}\:\wedge\:{x}+\mathrm{1}<\mathrm{0}\:\right) \\ $$ $${x}>−\mathrm{2}\:\wedge\:{x}>−\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:{or}\:{x}<−\mathrm{2}\:\wedge\:{x}<−\mathrm{1} \\ $$ $${x}>−\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{or}\:\:{x}<−\mathrm{2} \\ $$ $$ \\ $$
Commented bysandy_suhendra last updated on 05/Sep/16
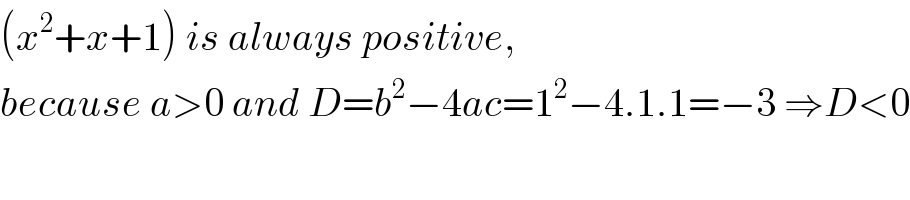
$$\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)\:{is}\:{always}\:{positive},\: \\ $$ $${because}\:{a}>\mathrm{0}\:{and}\:{D}={b}^{\mathrm{2}} −\mathrm{4}{ac}=\mathrm{1}^{\mathrm{2}} −\mathrm{4}.\mathrm{1}.\mathrm{1}=−\mathrm{3}\:\Rightarrow{D}<\mathrm{0} \\ $$
Commented byRasheed Soomro last updated on 05/Sep/16

$$\mathcal{TH}_{{n}} ^{\alpha} \mathcal{KS}! \\ $$
