
Question Number 7600 by Rohit last updated on 05/Sep/16
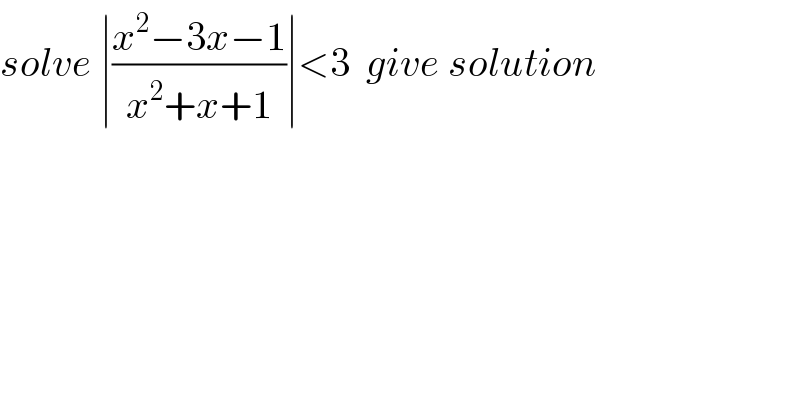
$${solve}\:\mid\frac{{x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\mid<\mathrm{3}\:\:{give}\:{solution} \\ $$
Answered by Yozzia last updated on 05/Sep/16
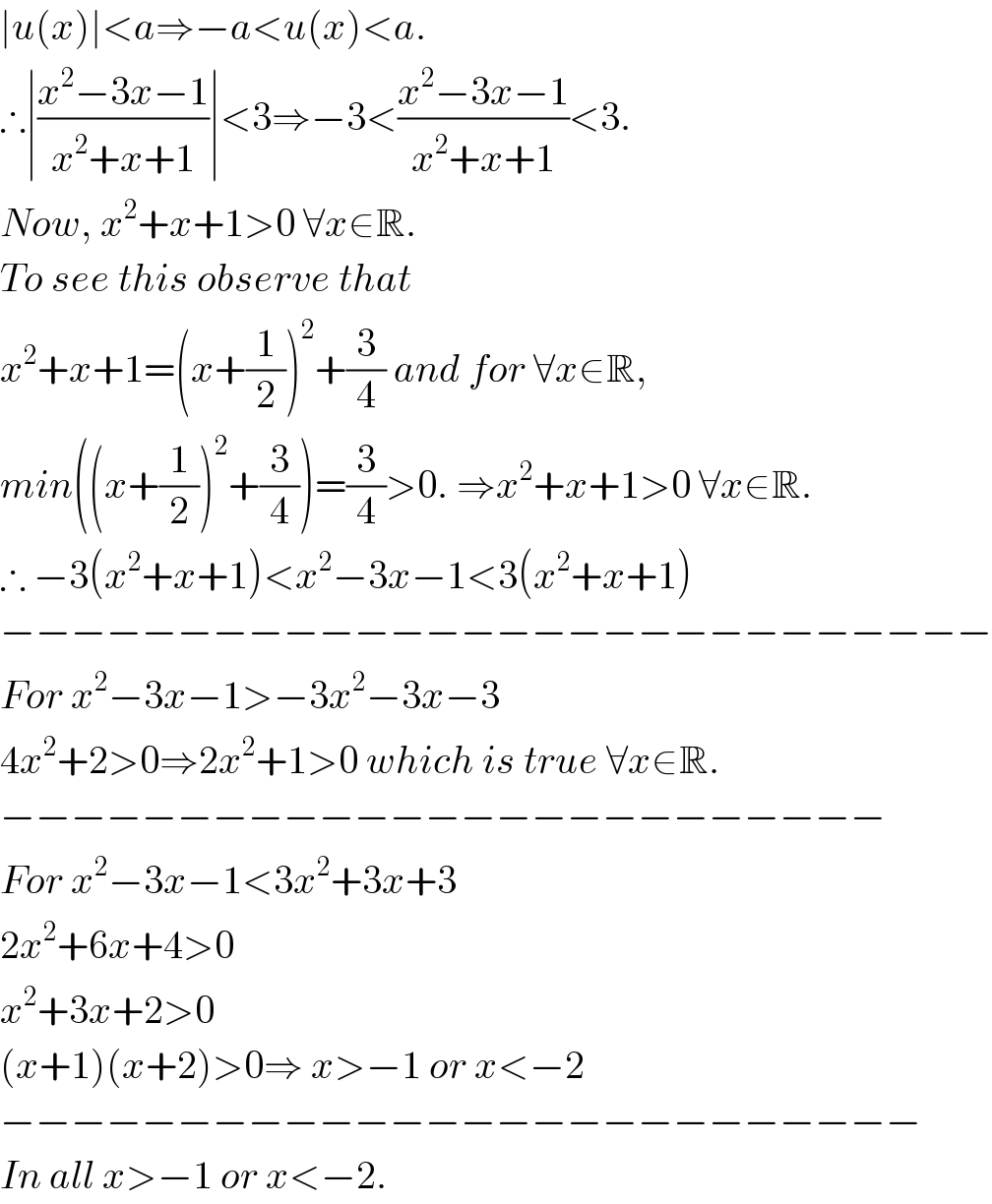
$$\mid{u}\left({x}\right)\mid<{a}\Rightarrow−{a}<{u}\left({x}\right)<{a}. \\ $$ $$\therefore\mid\frac{{x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\mid<\mathrm{3}\Rightarrow−\mathrm{3}<\frac{{x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}<\mathrm{3}. \\ $$ $${Now},\:{x}^{\mathrm{2}} +{x}+\mathrm{1}>\mathrm{0}\:\forall{x}\in\mathbb{R}. \\ $$ $${To}\:{see}\:{this}\:{observe}\:{that}\: \\ $$ $${x}^{\mathrm{2}} +{x}+\mathrm{1}=\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}\:{and}\:{for}\:\forall{x}\in\mathbb{R}, \\ $$ $${min}\left(\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}\right)=\frac{\mathrm{3}}{\mathrm{4}}>\mathrm{0}.\:\Rightarrow{x}^{\mathrm{2}} +{x}+\mathrm{1}>\mathrm{0}\:\forall{x}\in\mathbb{R}. \\ $$ $$\therefore\:−\mathrm{3}\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)<{x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{1}<\mathrm{3}\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right) \\ $$ $$−−−−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$ $${For}\:{x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{1}>−\mathrm{3}{x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{3} \\ $$ $$\mathrm{4}{x}^{\mathrm{2}} +\mathrm{2}>\mathrm{0}\Rightarrow\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}>\mathrm{0}\:{which}\:{is}\:{true}\:\forall{x}\in\mathbb{R}. \\ $$ $$−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$ $${For}\:{x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{1}<\mathrm{3}{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{3} \\ $$ $$\mathrm{2}{x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{4}>\mathrm{0} \\ $$ $${x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{2}>\mathrm{0} \\ $$ $$\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)>\mathrm{0}\Rightarrow\:{x}>−\mathrm{1}\:{or}\:{x}<−\mathrm{2} \\ $$ $$−−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$ $${In}\:{all}\:{x}>−\mathrm{1}\:{or}\:{x}<−\mathrm{2}. \\ $$
