
Question Number 7649 by Rohit last updated on 07/Sep/16
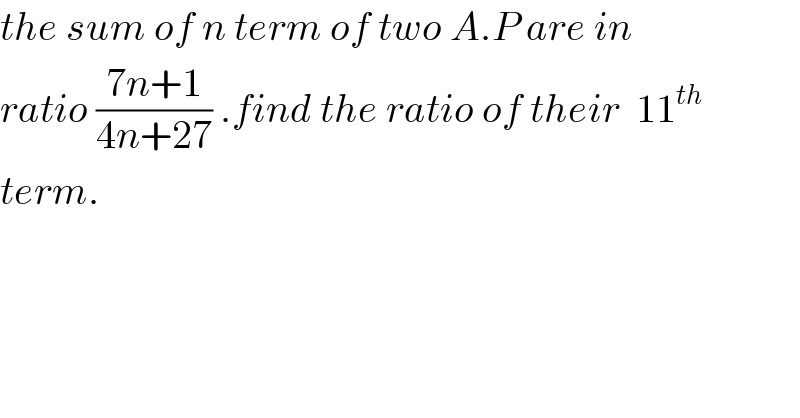
$${the}\:{sum}\:{of}\:{n}\:{term}\:{of}\:{two}\:{A}.{P}\:{are}\:{in}\: \\ $$$${ratio}\:\frac{\mathrm{7}{n}+\mathrm{1}}{\mathrm{4}{n}+\mathrm{27}}\:.{find}\:{the}\:{ratio}\:{of}\:{their}\:\:\mathrm{11}^{{th}} \\ $$$${term}. \\ $$
Commented by Rohit last updated on 07/Sep/16

$${answer}\:{plese}..... \\ $$
Answered by Rasheed Soomro last updated on 07/Sep/16
![Let a_(1 ) and d_1 are the first term and common difference of first AP respectively. And a_(2 ) and d_2 are the first term and common differnce of second AP respectively. −−−−−−−−−−−−− 11th terms of the two AP ′s are a_1 +(11−1)d_1 = a_1 +10d_1 and a_2 +(11−1)d_2 =a_2 +10d_2 . So we have to determine ((a_1 +10d_1 )/(a_2 +10d_2 )) −−−−−−−−−−−−−− The ratio of n terms of the two AP ′s is given by (((n/2)[2a_1 +(n−1)d_1 ])/((n/2)[2a_2 +(n−1)d_2 ]))= ((7n+1)/(4n+27)) ((2a_1 +(n−1)d_1 )/(2a_2 +(n−1)d_2 ))= ((7n+1)/(4n+27)) −−−−−−−−−−−−−−−− Let′s determine ratio of the sums of 21 terms of the two AP ′s ((2a_1 +(21−1)d_1 )/(2a_2 +(21−1)d_2 ))= ((7(21)+1)/(4(21)+27))=((148)/(111)) ((2a_1 +20d_1 )/(2a_2 +20d_2 ))=((148)/(111)) ((2(a_1 +10d_1 ))/(2(a_2 +10d_2 )))=((148)/(111)) ((a_1 +10d_1 )/(a_2 +10d_2 ))=((148)/(111)) ((11th term of the 1st AP)/(11th term of the 2nd AP))=((148)/(111))](Q7657.png)
$${Let}\:{a}_{\mathrm{1}\:} {and}\:{d}_{\mathrm{1}} \:{are}\:{the}\:{first}\:{term}\:{and}\:{common}\:{difference} \\ $$$$\:\:\:\:\:\:\:\:\:{of}\:{first}\:{AP}\:{respectively}. \\ $$$${And}\:{a}_{\mathrm{2}\:} {and}\:{d}_{\mathrm{2}} \:{are}\:{the}\:{first}\:{term}\:{and}\:{common}\:{differnce} \\ $$$$\:\:\:\:\:\:\:\:\:{of}\:\:{second}\:{AP}\:{respectively}. \\ $$$$−−−−−−−−−−−−− \\ $$$$\mathrm{11}{th}\:{terms}\:{of}\:{the}\:{two}\:{AP}\:'{s}\:\:{are}\:{a}_{\mathrm{1}} +\left(\mathrm{11}−\mathrm{1}\right){d}_{\mathrm{1}} =\:{a}_{\mathrm{1}} +\mathrm{10}{d}_{\mathrm{1}} \\ $$$${and}\:{a}_{\mathrm{2}} +\left(\mathrm{11}−\mathrm{1}\right){d}_{\mathrm{2}} ={a}_{\mathrm{2}} +\mathrm{10}{d}_{\mathrm{2}} .\:{So}\:{we}\:{have}\:{to}\:{determine}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{a}_{\mathrm{1}} +\mathrm{10}{d}_{\mathrm{1}} }{{a}_{\mathrm{2}} +\mathrm{10}{d}_{\mathrm{2}} } \\ $$$$−−−−−−−−−−−−−− \\ $$$${The}\:{ratio}\:{of}\:{n}\:{terms}\:{of}\:{the}\:{two}\:{AP}\:'{s}\:{is}\:{given}\:{by} \\ $$$$\frac{\frac{{n}}{\mathrm{2}}\left[\mathrm{2}{a}_{\mathrm{1}} +\left({n}−\mathrm{1}\right){d}_{\mathrm{1}} \right]}{\frac{{n}}{\mathrm{2}}\left[\mathrm{2}{a}_{\mathrm{2}} +\left({n}−\mathrm{1}\right){d}_{\mathrm{2}} \right]}=\:\frac{\mathrm{7}{n}+\mathrm{1}}{\mathrm{4}{n}+\mathrm{27}} \\ $$$$\frac{\mathrm{2}{a}_{\mathrm{1}} +\left({n}−\mathrm{1}\right){d}_{\mathrm{1}} }{\mathrm{2}{a}_{\mathrm{2}} +\left({n}−\mathrm{1}\right){d}_{\mathrm{2}} }=\:\frac{\mathrm{7}{n}+\mathrm{1}}{\mathrm{4}{n}+\mathrm{27}} \\ $$$$−−−−−−−−−−−−−−−− \\ $$$${Let}'{s}\:{determine}\:{ratio}\:{of}\:{the}\:{sums}\:{of}\:\mathrm{21}\:{terms}\:{of}\:{the} \\ $$$${two}\:{AP}\:'{s} \\ $$$$\frac{\mathrm{2}{a}_{\mathrm{1}} +\left(\mathrm{21}−\mathrm{1}\right){d}_{\mathrm{1}} }{\mathrm{2}{a}_{\mathrm{2}} +\left(\mathrm{21}−\mathrm{1}\right){d}_{\mathrm{2}} }=\:\frac{\mathrm{7}\left(\mathrm{21}\right)+\mathrm{1}}{\mathrm{4}\left(\mathrm{21}\right)+\mathrm{27}}=\frac{\mathrm{148}}{\mathrm{111}} \\ $$$$\frac{\mathrm{2}{a}_{\mathrm{1}} +\mathrm{20}{d}_{\mathrm{1}} }{\mathrm{2}{a}_{\mathrm{2}} +\mathrm{20}{d}_{\mathrm{2}} }=\frac{\mathrm{148}}{\mathrm{111}} \\ $$$$\frac{\mathrm{2}\left({a}_{\mathrm{1}} +\mathrm{10}{d}_{\mathrm{1}} \right)}{\mathrm{2}\left({a}_{\mathrm{2}} +\mathrm{10}{d}_{\mathrm{2}} \right)}=\frac{\mathrm{148}}{\mathrm{111}} \\ $$$$\frac{{a}_{\mathrm{1}} +\mathrm{10}{d}_{\mathrm{1}} }{{a}_{\mathrm{2}} +\mathrm{10}{d}_{\mathrm{2}} }=\frac{\mathrm{148}}{\mathrm{111}} \\ $$$$\frac{\mathrm{11}{th}\:{term}\:{of}\:{the}\:\mathrm{1}{st}\:{AP}}{\mathrm{11}{th}\:{term}\:{of}\:{the}\:\mathrm{2}{nd}\:{AP}}=\frac{\mathrm{148}}{\mathrm{111}} \\ $$$$ \\ $$
Commented by Rohit last updated on 08/Sep/16
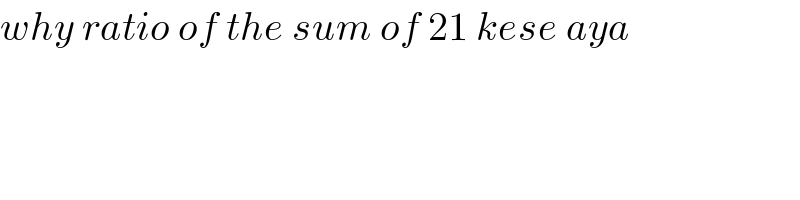
$${why}\:{ratio}\:{of}\:{the}\:{sum}\:{of}\:\mathrm{21}\:{kese}\:{aya} \\ $$
Commented by Rasheed Soomro last updated on 08/Sep/16
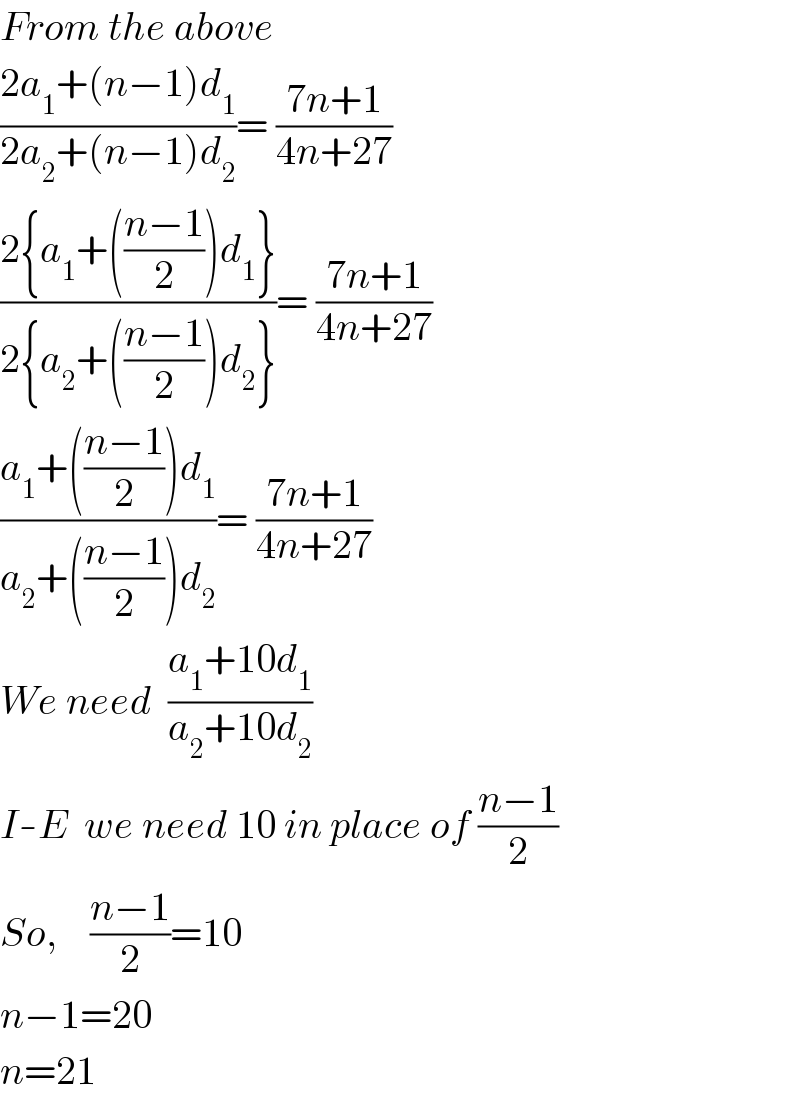
$${From}\:{the}\:{above} \\ $$$$\frac{\mathrm{2}{a}_{\mathrm{1}} +\left({n}−\mathrm{1}\right){d}_{\mathrm{1}} }{\mathrm{2}{a}_{\mathrm{2}} +\left({n}−\mathrm{1}\right){d}_{\mathrm{2}} }=\:\frac{\mathrm{7}{n}+\mathrm{1}}{\mathrm{4}{n}+\mathrm{27}} \\ $$$$\frac{\mathrm{2}\left\{{a}_{\mathrm{1}} +\left(\frac{{n}−\mathrm{1}}{\mathrm{2}}\right){d}_{\mathrm{1}} \right\}}{\mathrm{2}\left\{{a}_{\mathrm{2}} +\left(\frac{{n}−\mathrm{1}}{\mathrm{2}}\right){d}_{\mathrm{2}} \right\}}=\:\frac{\mathrm{7}{n}+\mathrm{1}}{\mathrm{4}{n}+\mathrm{27}} \\ $$$$\frac{{a}_{\mathrm{1}} +\left(\frac{{n}−\mathrm{1}}{\mathrm{2}}\right){d}_{\mathrm{1}} }{{a}_{\mathrm{2}} +\left(\frac{{n}−\mathrm{1}}{\mathrm{2}}\right){d}_{\mathrm{2}} }=\:\frac{\mathrm{7}{n}+\mathrm{1}}{\mathrm{4}{n}+\mathrm{27}} \\ $$$${We}\:{need}\:\:\frac{{a}_{\mathrm{1}} +\mathrm{10}{d}_{\mathrm{1}} }{{a}_{\mathrm{2}} +\mathrm{10}{d}_{\mathrm{2}} } \\ $$$${I}-{E}\:\:{we}\:{need}\:\mathrm{10}\:{in}\:{place}\:{of}\:\frac{{n}−\mathrm{1}}{\mathrm{2}} \\ $$$${So},\:\:\:\:\frac{{n}−\mathrm{1}}{\mathrm{2}}=\mathrm{10} \\ $$$${n}−\mathrm{1}=\mathrm{20} \\ $$$${n}=\mathrm{21} \\ $$
