Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 7743 by Tawakalitu. last updated on 13/Sep/16

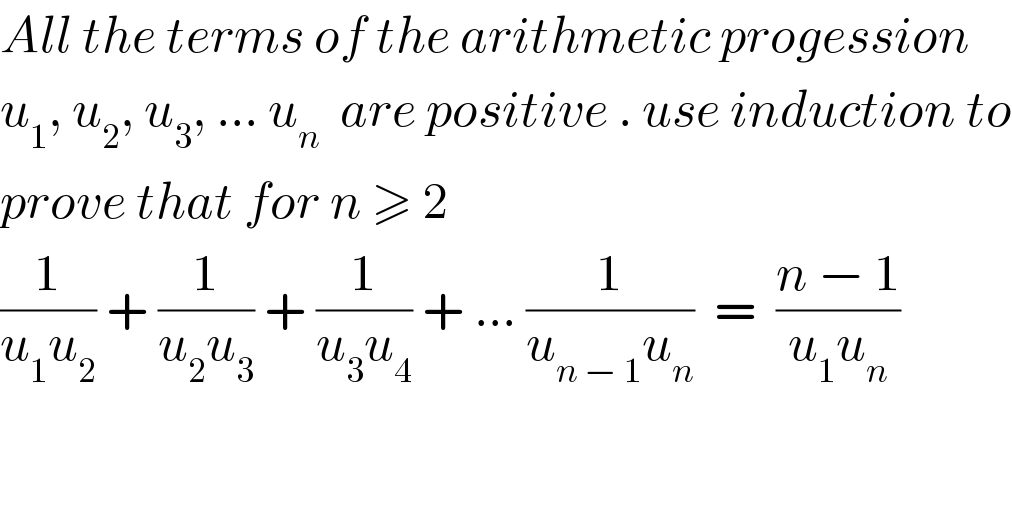
All the terms of the arithmetic progession u_1 , u_2 , u_3 , ... u_n are positive . use induction to prove that for n ≥ 2 (1/(u_1 u_2 )) + (1/(u_2 u_3 )) + (1/(u_3 u_4 )) + ... (1/(u_(n − 1) u_n )) = ((n − 1)/(u_1 u_n ))

$${All}\:{the}\:{terms}\:{of}\:{the}\:{arithmetic}\:{progession}\: \\ $$$${u}_{\mathrm{1}} ,\:{u}_{\mathrm{2}} ,\:{u}_{\mathrm{3}} ,\:...\:{u}_{{n}} \:\:{are}\:{positive}\:.\:{use}\:{induction}\:{to} \\ $$$${prove}\:{that}\:{for}\:{n}\:\geqslant\:\mathrm{2} \\ $$$$\frac{\mathrm{1}}{{u}_{\mathrm{1}} {u}_{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{{u}_{\mathrm{2}} {u}_{\mathrm{3}} }\:+\:\frac{\mathrm{1}}{{u}_{\mathrm{3}} {u}_{\mathrm{4}} }\:+\:...\:\frac{\mathrm{1}}{{u}_{{n}\:−\:\mathrm{1}} {u}_{{n}} }\:\:=\:\:\frac{{n}\:−\:\mathrm{1}}{{u}_{\mathrm{1}} {u}_{{n}} } \\ $$

Answered by Yozzia last updated on 13/Sep/16

Let P(n) denote the statement, ∀n∈N,n≥2, (1/(u_1 u_2 ))+(1/(u_2 u_3 ))+(1/(u_3 u_4 ))+...+(1/(u_(n−1) u_n ))=((n−1)/(u_1 u_n )) for u_1 ,u_2 ,...,u_n being an A.P with all terms positive. For n=2, P(2) says (1/(u_1 u_2 ))=((2−1)/(u_1 u_2 ))=(1/(u_1 u_2 )) which is true. Assume P(n) is true for some n=k,i.e Σ_(i=1) ^(k−1) (1/(u_i u_(i+1) ))=((k−1)/(u_1 u_k )). Σ_(i=1) ^(k−1) (1/(u_i u_(i+1) ))+(1/(u_k u_(k+1) ))=((k−1)/(u_1 u_k ))+(1/(u_k u_(k+1) )) Σ_(i=1) ^k (1/(u_i u_(i+1) ))=(1/u_k )(((k−1)/u_1 )+(1/u_(k+1) )) Σ_(i=1) ^k (1/(u_i u_(i+1) ))=(1/u_k )((((k−1)u_(k+1) +u_1 )/(u_1 u_(k+1) ))) For the A.P, u_t =u_1 +(t−1)d for t∈N, d=common difference. ∴ u_(k+1) =u_1 +kd Σ_(i=1) ^k (1/(u_i u_(i+1) ))=(1/u_k )((((k−1)(u_1 +kd)+u_1 )/(u_1 u_(k+1) ))) Σ_(i=1) ^k (1/(u_i u_(i+1) ))=(1/u_k )(((k(u_1 +kd)−u_1 −kd+u_1 )/(u_1 u_(k+1) ))) Σ_(i=1) ^k (1/(u_i u_(i+1) ))=(1/u_k )(((k(u_1 +kd−d))/(u_1 u_(k+1) )))=(1/u_k )×((k(u_1 +(k−1)d))/(u_1 u_(k+1) )) Σ_(i=1) ^k (1/(u_i u_(i+1) ))=(1/u_k )×((ku_k )/(u_1 u_(k+1) ))=(k/(u_1 u_(k+1) )) which is P(k+1) Therefore, if P(k) is true, then P(k+1) is true. Since P(2) is true then, by P.M.I, P(n) is true ∀n∈N,n≥2.

$${Let}\:{P}\left({n}\right)\:{denote}\:{the}\:{statement},\:\forall{n}\in\mathbb{N},{n}\geqslant\mathrm{2}, \\ $$$$\frac{\mathrm{1}}{{u}_{\mathrm{1}} {u}_{\mathrm{2}} }+\frac{\mathrm{1}}{{u}_{\mathrm{2}} {u}_{\mathrm{3}} }+\frac{\mathrm{1}}{{u}_{\mathrm{3}} {u}_{\mathrm{4}} }+...+\frac{\mathrm{1}}{{u}_{{n}−\mathrm{1}} {u}_{{n}} }=\frac{{n}−\mathrm{1}}{{u}_{\mathrm{1}} {u}_{{n}} } \\ $$$${for}\:{u}_{\mathrm{1}} ,{u}_{\mathrm{2}} ,...,{u}_{{n}} \:{being}\:{an}\:{A}.{P}\:{with}\:{all}\:{terms}\:{positive}. \\ $$$${For}\:{n}=\mathrm{2},\:{P}\left(\mathrm{2}\right)\:{says}\:\frac{\mathrm{1}}{{u}_{\mathrm{1}} {u}_{\mathrm{2}} }=\frac{\mathrm{2}−\mathrm{1}}{{u}_{\mathrm{1}} {u}_{\mathrm{2}} }=\frac{\mathrm{1}}{{u}_{\mathrm{1}} {u}_{\mathrm{2}} } \\ $$$${which}\:{is}\:{true}. \\ $$$${Assume}\:{P}\left({n}\right)\:{is}\:{true}\:{for}\:{some}\:{n}={k},{i}.{e} \\ $$$$\underset{{i}=\mathrm{1}} {\overset{{k}−\mathrm{1}} {\sum}}\frac{\mathrm{1}}{{u}_{{i}} {u}_{{i}+\mathrm{1}} }=\frac{{k}−\mathrm{1}}{{u}_{\mathrm{1}} {u}_{{k}} }. \\ $$$$\underset{{i}=\mathrm{1}} {\overset{{k}−\mathrm{1}} {\sum}}\frac{\mathrm{1}}{{u}_{{i}} {u}_{{i}+\mathrm{1}} }+\frac{\mathrm{1}}{{u}_{{k}} {u}_{{k}+\mathrm{1}} }=\frac{{k}−\mathrm{1}}{{u}_{\mathrm{1}} {u}_{{k}} }+\frac{\mathrm{1}}{{u}_{{k}} {u}_{{k}+\mathrm{1}} } \\ $$$$\underset{{i}=\mathrm{1}} {\overset{{k}} {\sum}}\frac{\mathrm{1}}{{u}_{{i}} {u}_{{i}+\mathrm{1}} }=\frac{\mathrm{1}}{{u}_{{k}} }\left(\frac{{k}−\mathrm{1}}{{u}_{\mathrm{1}} }+\frac{\mathrm{1}}{{u}_{{k}+\mathrm{1}} }\right) \\ $$$$\underset{{i}=\mathrm{1}} {\overset{{k}} {\sum}}\frac{\mathrm{1}}{{u}_{{i}} {u}_{{i}+\mathrm{1}} }=\frac{\mathrm{1}}{{u}_{{k}} }\left(\frac{\left({k}−\mathrm{1}\right){u}_{{k}+\mathrm{1}} +{u}_{\mathrm{1}} }{{u}_{\mathrm{1}} {u}_{{k}+\mathrm{1}} }\right) \\ $$$${For}\:{the}\:{A}.{P},\:{u}_{{t}} ={u}_{\mathrm{1}} +\left({t}−\mathrm{1}\right){d}\:{for}\:{t}\in\mathbb{N},\:{d}={common}\:{difference}. \\ $$$$\therefore\:{u}_{{k}+\mathrm{1}} ={u}_{\mathrm{1}} +{kd} \\ $$$$\underset{{i}=\mathrm{1}} {\overset{{k}} {\sum}}\frac{\mathrm{1}}{{u}_{{i}} {u}_{{i}+\mathrm{1}} }=\frac{\mathrm{1}}{{u}_{{k}} }\left(\frac{\left({k}−\mathrm{1}\right)\left({u}_{\mathrm{1}} +{kd}\right)+{u}_{\mathrm{1}} }{{u}_{\mathrm{1}} {u}_{{k}+\mathrm{1}} }\right) \\ $$$$\underset{{i}=\mathrm{1}} {\overset{{k}} {\sum}}\frac{\mathrm{1}}{{u}_{{i}} {u}_{{i}+\mathrm{1}} }=\frac{\mathrm{1}}{{u}_{{k}} }\left(\frac{{k}\left({u}_{\mathrm{1}} +{kd}\right)−{u}_{\mathrm{1}} −{kd}+{u}_{\mathrm{1}} }{{u}_{\mathrm{1}} {u}_{{k}+\mathrm{1}} }\right) \\ $$$$\underset{{i}=\mathrm{1}} {\overset{{k}} {\sum}}\frac{\mathrm{1}}{{u}_{{i}} {u}_{{i}+\mathrm{1}} }=\frac{\mathrm{1}}{{u}_{{k}} }\left(\frac{{k}\left({u}_{\mathrm{1}} +{kd}−{d}\right)}{{u}_{\mathrm{1}} {u}_{{k}+\mathrm{1}} }\right)=\frac{\mathrm{1}}{{u}_{{k}} }×\frac{{k}\left({u}_{\mathrm{1}} +\left({k}−\mathrm{1}\right){d}\right)}{{u}_{\mathrm{1}} {u}_{{k}+\mathrm{1}} } \\ $$$$\underset{{i}=\mathrm{1}} {\overset{{k}} {\sum}}\frac{\mathrm{1}}{{u}_{{i}} {u}_{{i}+\mathrm{1}} }=\frac{\mathrm{1}}{{u}_{{k}} }×\frac{{ku}_{{k}} }{{u}_{\mathrm{1}} {u}_{{k}+\mathrm{1}} }=\frac{{k}}{{u}_{\mathrm{1}} {u}_{{k}+\mathrm{1}} }\:{which}\:{is}\:{P}\left({k}+\mathrm{1}\right) \\ $$$${Therefore},\:{if}\:{P}\left({k}\right)\:{is}\:{true},\:{then}\:{P}\left({k}+\mathrm{1}\right)\:{is}\:{true}. \\ $$$${Since}\:{P}\left(\mathrm{2}\right)\:{is}\:{true}\:{then},\:{by}\:{P}.{M}.{I},\: \\ $$$${P}\left({n}\right)\:{is}\:{true}\:\forall{n}\in\mathbb{N},{n}\geqslant\mathrm{2}. \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by Tawakalitu. last updated on 13/Sep/16

Wow, Thank you so much.

$${Wow},\:{Thank}\:{you}\:{so}\:{much}. \\ $$

Commented by Tawakalitu. last updated on 13/Sep/16

I really appreciate

$${I}\:\:{really}\:{appreciate} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com