Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 77464 by naka3546 last updated on 06/Jan/20

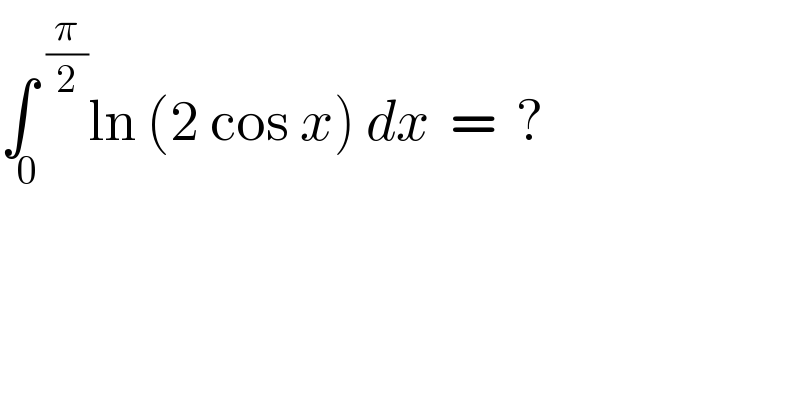
∫_( 0) ^(π/2) ln (2 cos x) dx = ?

$$\underset{\:\:\mathrm{0}} {\int}\:\overset{\frac{\pi}{\mathrm{2}}} {\:}\mathrm{ln}\:\left(\mathrm{2}\:\mathrm{cos}\:{x}\right)\:{dx}\:\:=\:\:? \\ $$

Commented by kaivan.ahmadi last updated on 06/Jan/20

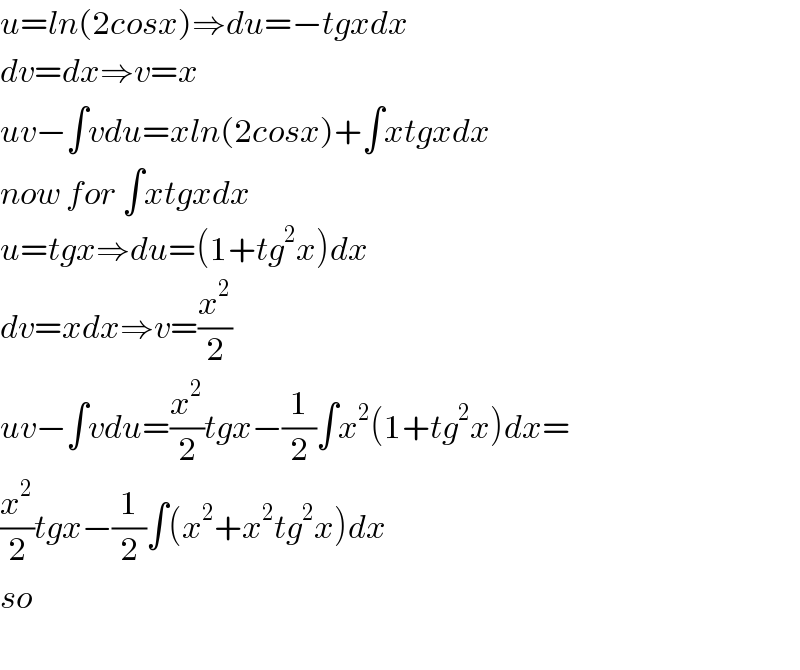
u=ln(2cosx)⇒du=−tgxdx dv=dx⇒v=x uv−∫vdu=xln(2cosx)+∫xtgxdx now for ∫xtgxdx u=tgx⇒du=(1+tg^2 x)dx dv=xdx⇒v=(x^2 /2) uv−∫vdu=(x^2 /2)tgx−(1/2)∫x^2 (1+tg^2 x)dx= (x^2 /2)tgx−(1/2)∫(x^2 +x^2 tg^2 x)dx so

$${u}={ln}\left(\mathrm{2}{cosx}\right)\Rightarrow{du}=−{tgxdx} \\ $$$${dv}={dx}\Rightarrow{v}={x} \\ $$$${uv}−\int{vdu}={xln}\left(\mathrm{2}{cosx}\right)+\int{xtgxdx} \\ $$$${now}\:{for}\:\int{xtgxdx} \\ $$$${u}={tgx}\Rightarrow{du}=\left(\mathrm{1}+{tg}^{\mathrm{2}} {x}\right){dx} \\ $$$${dv}={xdx}\Rightarrow{v}=\frac{{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${uv}−\int{vdu}=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}{tgx}−\frac{\mathrm{1}}{\mathrm{2}}\int{x}^{\mathrm{2}} \left(\mathrm{1}+{tg}^{\mathrm{2}} {x}\right){dx}= \\ $$$$\frac{{x}^{\mathrm{2}} }{\mathrm{2}}{tgx}−\frac{\mathrm{1}}{\mathrm{2}}\int\left({x}^{\mathrm{2}} +{x}^{\mathrm{2}} {tg}^{\mathrm{2}} {x}\right){dx} \\ $$$${so} \\ $$$$ \\ $$

Commented by MJS last updated on 06/Jan/20

sorry but this is wrong I don′t think it′s possible to solve this using elementary calculus

$$\mathrm{sorry}\:\mathrm{but}\:\mathrm{this}\:\mathrm{is}\:\mathrm{wrong} \\ $$$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{it}'\mathrm{s}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{this}\:\mathrm{using} \\ $$$$\mathrm{elementary}\:\mathrm{calculus} \\ $$

Commented by kaivan.ahmadi last updated on 06/Jan/20

if F(x)=xln(2cosx)+(1/2)(x^2 tgx−x+tg^(−1) x) then F ′(x)=ln(2cosx) so ∫ln(2cosx)dx=F(x)+C

$${if}\:{F}\left({x}\right)={xln}\left(\mathrm{2}{cosx}\right)+\frac{\mathrm{1}}{\mathrm{2}}\left({x}^{\mathrm{2}} {tgx}−{x}+{tg}^{−\mathrm{1}} {x}\right) \\ $$$${then} \\ $$$${F}\:'\left({x}\right)={ln}\left(\mathrm{2}{cosx}\right) \\ $$$${so}\:\int{ln}\left(\mathrm{2}{cosx}\right){dx}={F}\left({x}\right)+{C} \\ $$

Commented by MJS last updated on 06/Jan/20

but (d/dx)[xln (2cos x) +(1/2)(x^2 tan x −x+tan x)]= =ln (2cos x) +(1/2)(tan^2 x +(x^2 /(cos^2 x)))

$$\mathrm{but} \\ $$$$\frac{{d}}{{dx}}\left[{x}\mathrm{ln}\:\left(\mathrm{2cos}\:{x}\right)\:+\frac{\mathrm{1}}{\mathrm{2}}\left({x}^{\mathrm{2}} \mathrm{tan}\:{x}\:−{x}+\mathrm{tan}\:{x}\right)\right]= \\ $$$$=\mathrm{ln}\:\left(\mathrm{2cos}\:{x}\right)\:+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{tan}^{\mathrm{2}} \:{x}\:+\frac{{x}^{\mathrm{2}} }{\mathrm{cos}^{\mathrm{2}} \:{x}}\right) \\ $$

Commented by mathmax by abdo last updated on 06/Jan/20

∫_0 ^(π/2) ln(2cosx)dx =(π/2)ln(2)+∫_0 ^(π/2) ln(cosx)dx we have proved that ∫_0 ^(π/2) ln(cosx)dx =−(π/2)ln(2) ⇒∫_0 ^(π/2) ln(2cosx)dx =0

$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\mathrm{2}{cosx}\right){dx}\:=\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({cosx}\right){dx}\:{we}\:{have}\:{proved}\:{that} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({cosx}\right){dx}\:=−\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\:\Rightarrow\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\mathrm{2}{cosx}\right){dx}\:=\mathrm{0} \\ $$

Commented by mathmax by abdo last updated on 06/Jan/20

let f(a)=∫_0 ^(π/2) ln(acosx)dx with a>0 we have f^′ (a) =∫_0 ^(π/2) ((cosx)/(acosx))dx =(π/(2a)) ⇒f(a) =(π/2)ln(a)+c f(1)=∫_0 ^(π/2) ln(cosx)dx =−(π/2)ln(2)=c ⇒ ∫_0 ^(π/2) ln(acosx)dx =(π/2)ln(a)−(π/2)ln(2) ⇒ ∫_0 ^(π/2) ln(2cosx)dx =0

$${let}\:{f}\left({a}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({acosx}\right){dx}\:{with}\:{a}>\mathrm{0}\:{we}\:{have} \\ $$$${f}^{'} \left({a}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{cosx}}{{acosx}}{dx}\:=\frac{\pi}{\mathrm{2}{a}}\:\Rightarrow{f}\left({a}\right)\:=\frac{\pi}{\mathrm{2}}{ln}\left({a}\right)+{c} \\ $$$${f}\left(\mathrm{1}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({cosx}\right){dx}\:=−\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)={c}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({acosx}\right){dx}\:=\frac{\pi}{\mathrm{2}}{ln}\left({a}\right)−\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\mathrm{2}{cosx}\right){dx}\:=\mathrm{0} \\ $$

Commented by kaivan.ahmadi last updated on 06/Jan/20

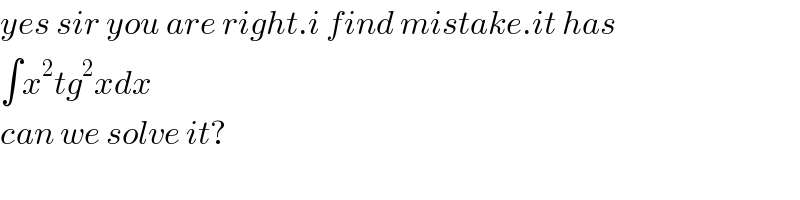
yes sir you are right.i find mistake.it has ∫x^2 tg^2 xdx can we solve it?

$${yes}\:{sir}\:{you}\:{are}\:{right}.{i}\:{find}\:{mistake}.{it}\:{has} \\ $$$$\int{x}^{\mathrm{2}} {tg}^{\mathrm{2}} {xdx} \\ $$$${can}\:{we}\:{solve}\:{it}? \\ $$

Answered by MJS last updated on 06/Jan/20

∫ln (2cos x) dx= [t=−ix → dx=i dt] =−i∫tdt+i∫ln (e^(2t) +1) dt ∫ln (e^(2t) +1) dt= [u=−e^(2t) → dt=−(dx/(2e^(2x) ))] =(1/2)∫((ln (1−u))/u)du=−(1/2)∫−((ln (1−u))/u)du= =−(1/2)Li_2 u Li_2 x is the dilogarithm with Li_2 x =Σ_(n=1) ^∞ (x^n /n^2 )

$$\int\mathrm{ln}\:\left(\mathrm{2cos}\:{x}\right)\:{dx}= \\ $$$$\:\:\:\:\:\left[{t}=−\mathrm{i}{x}\:\rightarrow\:{dx}=\mathrm{i}\:{dt}\right] \\ $$$$=−\mathrm{i}\int{tdt}+\mathrm{i}\int\mathrm{ln}\:\left(\mathrm{e}^{\mathrm{2}{t}} +\mathrm{1}\right)\:{dt} \\ $$$$\int\mathrm{ln}\:\left(\mathrm{e}^{\mathrm{2}{t}} +\mathrm{1}\right)\:{dt}= \\ $$$$\:\:\:\:\:\left[{u}=−\mathrm{e}^{\mathrm{2}{t}} \:\rightarrow\:{dt}=−\frac{{dx}}{\mathrm{2e}^{\mathrm{2}{x}} }\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{ln}\:\left(\mathrm{1}−{u}\right)}{{u}}{du}=−\frac{\mathrm{1}}{\mathrm{2}}\int−\frac{\mathrm{ln}\:\left(\mathrm{1}−{u}\right)}{{u}}{du}= \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Li}_{\mathrm{2}} \:{u} \\ $$$$\mathrm{Li}_{\mathrm{2}} \:{x}\:\mathrm{is}\:\mathrm{the}\:\mathrm{dilogarithm}\:\mathrm{with}\:\mathrm{Li}_{\mathrm{2}} \:{x}\:=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}^{\mathrm{2}} } \\ $$

Answered by Kunal12588 last updated on 07/Jan/20

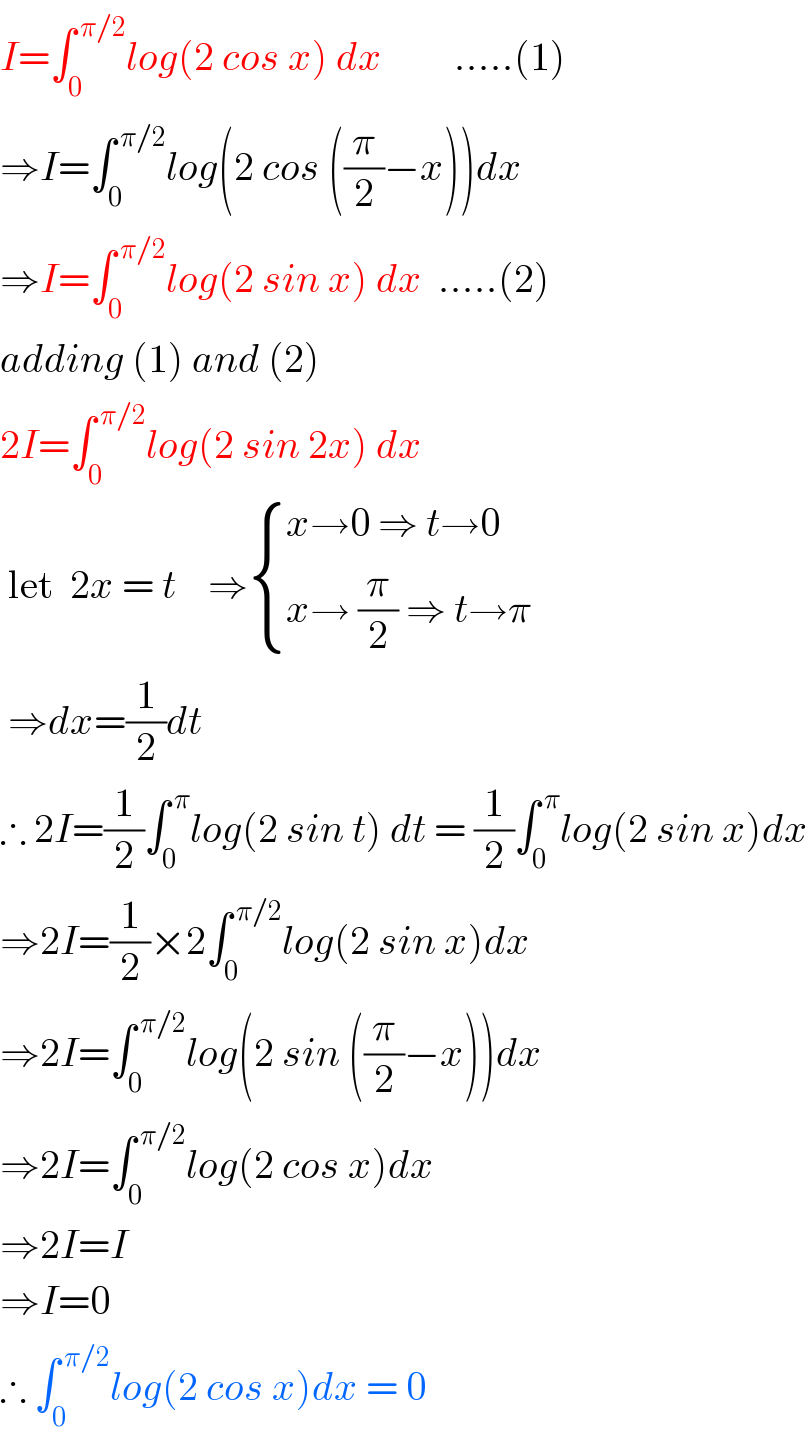
I=∫_0 ^( π/2) log(2 cos x) dx .....(1) ⇒I=∫_0 ^( π/2) log(2 cos ((π/2)−x))dx ⇒I=∫_0 ^( π/2) log(2 sin x) dx .....(2) adding (1) and (2) 2I=∫_0 ^( π/2) log(2 sin 2x) dx let 2x = t ⇒ { ((x→0 ⇒ t→0)),((x→ (π/2) ⇒ t→π)) :} ⇒dx=(1/2)dt ∴ 2I=(1/2)∫_0 ^( π) log(2 sin t) dt = (1/2)∫_0 ^( π) log(2 sin x)dx ⇒2I=(1/2)×2∫_0 ^( π/2) log(2 sin x)dx ⇒2I=∫_0 ^( π/2) log(2 sin ((π/2)−x))dx ⇒2I=∫_0 ^( π/2) log(2 cos x)dx ⇒2I=I ⇒I=0 ∴ ∫_0 ^( π/2) log(2 cos x)dx = 0

$${I}=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} {log}\left(\mathrm{2}\:{cos}\:{x}\right)\:{dx}\:\:\:\:\:\:\:\:\:.....\left(\mathrm{1}\right) \\ $$$$\Rightarrow{I}=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} {log}\left(\mathrm{2}\:{cos}\:\left(\frac{\pi}{\mathrm{2}}−{x}\right)\right){dx} \\ $$$$\Rightarrow{I}=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} {log}\left(\mathrm{2}\:{sin}\:{x}\right)\:{dx}\:\:.....\left(\mathrm{2}\right) \\ $$$${adding}\:\left(\mathrm{1}\right)\:{and}\:\left(\mathrm{2}\right) \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} {log}\left(\mathrm{2}\:{sin}\:\mathrm{2}{x}\right)\:{dx} \\ $$$$\:\mathrm{let}\:\:\mathrm{2}{x}\:=\:{t}\:\:\:\:\Rightarrow\begin{cases}{{x}\rightarrow\mathrm{0}\:\Rightarrow\:{t}\rightarrow\mathrm{0}}\\{{x}\rightarrow\:\frac{\pi}{\mathrm{2}}\:\Rightarrow\:{t}\rightarrow\pi}\end{cases} \\ $$$$\:\Rightarrow{dx}=\frac{\mathrm{1}}{\mathrm{2}}{dt} \\ $$$$\therefore\:\mathrm{2}{I}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\pi} {log}\left(\mathrm{2}\:{sin}\:{t}\right)\:{dt}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\pi} {log}\left(\mathrm{2}\:{sin}\:{x}\right){dx} \\ $$$$\Rightarrow\mathrm{2}{I}=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} {log}\left(\mathrm{2}\:{sin}\:{x}\right){dx} \\ $$$$\Rightarrow\mathrm{2}{I}=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} {log}\left(\mathrm{2}\:{sin}\:\left(\frac{\pi}{\mathrm{2}}−{x}\right)\right){dx} \\ $$$$\Rightarrow\mathrm{2}{I}=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} {log}\left(\mathrm{2}\:{cos}\:{x}\right){dx} \\ $$$$\Rightarrow\mathrm{2}{I}={I} \\ $$$$\Rightarrow{I}=\mathrm{0} \\ $$$$\therefore\:\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} {log}\left(\mathrm{2}\:{cos}\:{x}\right){dx}\:=\:\mathrm{0} \\ $$

Answered by Kunal12588 last updated on 07/Jan/20

I=∫_0 ^( π/2) log(a cos x)dx ⇒I=∫_0 ^( π/2) log(a sin x)dx ⇒2I=∫_0 ^( π/2) log(a^2 sin x cos x)dx ⇒2I=∫_0 ^( π/2) log((a^2 /2) sin 2x)dx ⇒2I=log((a^2 /2))∫_0 ^( π/2) dx+∫_0 ^( π/2) log(sin 2x) dx ⇒2I=(π/2)log((a^2 /2))+(1/2)∫_0 ^( π) log(sin x) dx ⇒2I=(π/2)log((a^2 /2))+(1/2)×2∫_0 ^( π/2) log(sin x) dx ⇒2I=(π/2)log((a^2 /2))+∫_0 ^( π/2) log(cos x) dx ⇒2I=(π/2)log((a^2 /2))−(π/2)log(2) ⇒I=(π/4)log((a^2 /2))−(π/4)log(2) ⇒I=(π/4)log((a^2 /4))=(π/2)log((a/2)) f(a)=∫_0 ^( π/2) log(a cos x) dx=(π/2)log((a/2)) f(1)=(π/2)log((1/2))=−(π/2)log(2) f(2)=(π/2)log(1)=0 f(3)=(π/2)log((3/2)) f(4)=(π/2)log(2) ⋮

$${I}=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} {log}\left({a}\:{cos}\:{x}\right){dx} \\ $$$$\Rightarrow{I}=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} {log}\left({a}\:{sin}\:{x}\right){dx} \\ $$$$\Rightarrow\mathrm{2}{I}=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} {log}\left({a}^{\mathrm{2}} \:{sin}\:{x}\:{cos}\:{x}\right){dx} \\ $$$$\Rightarrow\mathrm{2}{I}=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} {log}\left(\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\:{sin}\:\mathrm{2}{x}\right){dx} \\ $$$$\Rightarrow\mathrm{2}{I}={log}\left(\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\right)\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} {dx}+\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} {log}\left({sin}\:\mathrm{2}{x}\right)\:{dx} \\ $$$$\Rightarrow\mathrm{2}{I}=\frac{\pi}{\mathrm{2}}{log}\left(\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\pi} \:{log}\left({sin}\:{x}\right)\:{dx} \\ $$$$\Rightarrow\mathrm{2}{I}=\frac{\pi}{\mathrm{2}}{log}\left(\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \:{log}\left({sin}\:{x}\right)\:{dx} \\ $$$$\Rightarrow\mathrm{2}{I}=\frac{\pi}{\mathrm{2}}{log}\left(\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\right)+\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \:{log}\left({cos}\:{x}\right)\:{dx} \\ $$$$\Rightarrow\mathrm{2}{I}=\frac{\pi}{\mathrm{2}}{log}\left(\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\right)−\frac{\pi}{\mathrm{2}}{log}\left(\mathrm{2}\right) \\ $$$$\Rightarrow{I}=\frac{\pi}{\mathrm{4}}{log}\left(\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\right)−\frac{\pi}{\mathrm{4}}{log}\left(\mathrm{2}\right) \\ $$$$\Rightarrow{I}=\frac{\pi}{\mathrm{4}}{log}\left(\frac{{a}^{\mathrm{2}} }{\mathrm{4}}\right)=\frac{\pi}{\mathrm{2}}{log}\left(\frac{{a}}{\mathrm{2}}\right) \\ $$$${f}\left({a}\right)=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} {log}\left({a}\:{cos}\:{x}\right)\:{dx}=\frac{\pi}{\mathrm{2}}{log}\left(\frac{{a}}{\mathrm{2}}\right) \\ $$$${f}\left(\mathrm{1}\right)=\frac{\pi}{\mathrm{2}}{log}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=−\frac{\pi}{\mathrm{2}}{log}\left(\mathrm{2}\right) \\ $$$${f}\left(\mathrm{2}\right)=\frac{\pi}{\mathrm{2}}{log}\left(\mathrm{1}\right)=\mathrm{0} \\ $$$${f}\left(\mathrm{3}\right)=\frac{\pi}{\mathrm{2}}{log}\left(\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$${f}\left(\mathrm{4}\right)=\frac{\pi}{\mathrm{2}}{log}\left(\mathrm{2}\right) \\ $$$$\vdots \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com