∫_( 0) ^( 1) log(((1 + x + x^2 + x^3 + x^4 )/(√(1 + (1/x) + (1/x^2 ) + (1/x^3 ) + (1/x^4 ))))) dx


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 77570 by TawaTawa last updated on 08/Jan/20

$\int_{0}^{1} \log (\frac{1 + x + x^{2} + x^{3} + x^{4}}{\sqrt{1 + \frac{1}{x} + \frac{1}{x^{2}} + \frac{1}{x^{3}} + \frac{1}{x^{4}}}}) dx$
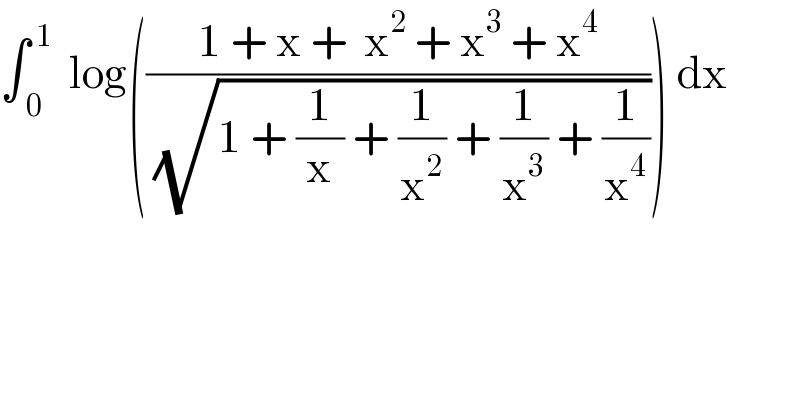
	Answered by MJS last updated on 08/Jan/20

	$= \underset{0}{\int^{1}} \ln (x^{2} \sqrt{x^{4} + x^{3} + x^{2} + x + 1}) d x =$ $= 2 \underset{0}{\int^{1}} \ln x d x + \frac{1}{2} \underset{0}{\int^{1}} \ln (x^{4} + x^{3} + x^{2} + x + 1) d x$ $2 \underset{0}{\int^{1}} \ln x d x = 2 {[x (\ln x - 1)]}_{0}^{1} =$ $[\lim_{x \to 0} x (\ln x - 1) = 0]$ $= - 2$ $\frac{1}{2} \underset{0}{\int^{1}} \ln (x^{4} + x^{3} + x^{2} + x + 1) d x =$ $[α_{j} = e^{i \frac{2 π j}{5}}; j = 1, 2, 3, 4]$ $= \frac{1}{2} \underset{0}{\int^{1}} \ln (\underset{j = 1}{\prod^{4}} (x - α_{j})) d x =$ $= \frac{1}{2} \underset{j = 1}{\sum^{4}} (\underset{0}{\int^{1}} \ln (x - α_{j}) d x) =$ $= \frac{1}{2} {[\underset{j = 1}{\sum^{4}} ((x - α_{j}) \ln (x - α_{j})) - 2 x]}_{0}^{1} = . . .$ $. . . = \frac{\sqrt{5}}{4} \ln \frac{1 + \sqrt{5}}{2} + \frac{5}{8} \ln 5 + \frac{\sqrt{25 + 10 \sqrt{5}}}{20} π - 2$ $\Rightarrow$ $answer is \frac{\sqrt{5}}{4} \ln \frac{1 + \sqrt{5}}{2} + \frac{5}{8} \ln 5 + \frac{\sqrt{25 + 10 \sqrt{5}}}{20} π - 4$
	Commented by TawaTawa last updated on 08/Jan/20

	$God bless you sir .$
	Commented by TawaTawa last updated on 12/Jan/20

	$Please sir . How did you get : e^{i \frac{2 π j}{5}}; j = 1, 2, 3, 4$
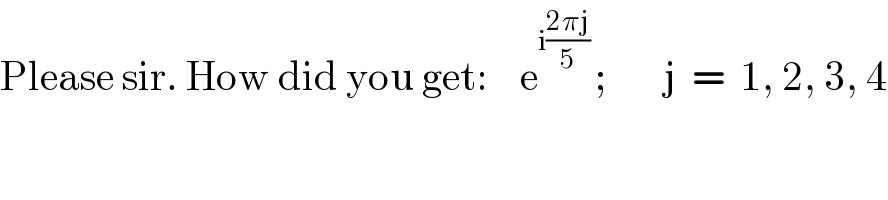
	Commented by MJS last updated on 12/Jan/20

	$(x^{4} + x^{3} + x^{2} + x + 1) (x - 1) = x^{5} - 1$ $\Rightarrow the roots are the 5^{th} roots of unity$ $= e^{i \frac{2 π j}{5}} with j = 0, 1, 2, 3, 4 but j = 0 \Leftrightarrow x - 1 = 0$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum