Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 77603 by kaivan.ahmadi last updated on 08/Jan/20

$$\int \frac{10x^2-8x+1}{x^4-x^3-x+1}dx$$$$$$

Commented by mathmax by abdo last updated on 08/Jan/20

$$letI=\int \frac{10x^2-8x+1}{x^4-x^3-x+1}dx\Rightarrow I=\int F\left(x\right)dxwehave{x}^4-x^3-x+1=$$$$x^3(x-1)-(x-1)=(x-1)(x^3-1)={(x-1)}^2(x^2+x+1)\Rightarrow$$$$F\left(x\right)=\frac{10x^2-8x+1}{{(x-1)}^2(x^2+x+1)}=\frac{a}{x-1}+\frac{b}{{(x-1)}^2}+\frac{cx+d}{x^2+x+1}$$$$b={(x-1)}^{2}F\left(x\right){\mid }_{x=1}=\frac{3}{3}=1$$$${lim}_{x\to +\mathrm{\infty }}xF\left(x\right)=0=a+c\Rightarrow c=-a\Rightarrow$$$$F\left(x\right)=\frac{a}{x-1}+\frac{1}{{(x-1)}^2}+\frac{-ax+d}{x^2+x+1}$$$$F\left(0\right)=1=-a+1+d\Rightarrow d=a\Rightarrow F\left(x\right)=\frac{a}{x-1}+\frac{1}{{(x-1)}^2}+\frac{-ax+a}{x^2+x+1}$$$$F(-1)=\frac{19}{4}=-\frac{a}{2}+\frac{1}{4}+\frac{2a}{1}\Rightarrow 19=-2a+1+8a\Rightarrow 18=6a\Rightarrow a=3$$$$\Rightarrow F\left(x\right)=\frac{3}{x-1}+\frac{1}{{(x-1)}^2}+\frac{-3x+3}{x^2+x+1}\Rightarrow$$$$I=3\int \frac{dx}{x-1}+\int \frac{dx}{{(x-1)}^2}-\frac{3}{2}\int \frac{2x-2}{x^2+x+1}dx$$$$=3ln\mid x-1\mid -\frac{1}{x-1}-\frac{3}{2}\int \frac{2x+1-3}{x^2+x+1}dx$$$$=3ln\mid x-1\mid -\frac{1}{x-1}-\frac{3}{2}ln(x^2+x+1)+\frac{9}{2}\int \frac{dx}{x^2+x+1}wehave$$$$\int \frac{dx}{x^2+x+1}=\int \frac{dx}{{(x+\frac{1}{2})}^2+\frac{3}{4}}{=}_{x+\frac{1}{2}=\frac{\sqrt{3}}{2}u}\frac{4}{3}\int \frac{1}{u^2+1}\times \frac{\sqrt{3}}{2}du$$$$=\frac{2}{\sqrt{3}}arctan\left(\frac{2x+1}{\sqrt{3}}\right)\Rightarrow$$$$I=3ln\mid x-1\mid -\frac{1}{x-1}+3\sqrt{3}arctan\left(\frac{2x+1}{\sqrt{3}}\right)+C.$$

Answered by Kunal12588 last updated on 08/Jan/20

$$x^4-x^3-x+1=x(x^3-1)-(x^3-1)$$$$=(x-1)(x^3-1)$$$$={(x-1)}^2(x^2+x+1)$$$$\frac{10x^2-8x+1}{{(x-1)}^2(x^2+x+1)}=\frac{a}{(x-1)}+\frac{b}{{(x-1)}^2}+\frac{cx+d}{(x^2+x+1)}$$$$\Rightarrow 10x^2-8x+1=a(x^4-x^3-x+1)+b(x^3-1)$$$$+(cx+d){(x-1)}^3$$$$10x^2-8x+1=\{\begin{array}{l}{ax}^4+(-a+b)x^3-ax+(a-b)\\ +(cx+d)(x^3-3x^2+3x-1)\end{array}$$$$10x^2-8x+1=\{\begin{array}{l}{ax}^4+(-a+b)x^3-ax+(a-b)\\ +{cx}^4+(-3c+d)x^3+(3c-3d)x^2\\ +(-c+3d)x-d\end{array}$$$$10x^2-8x+1=\{\begin{array}{l}(a+c)x^4+(-a+b-3c+d)x^3\\ +(3c-3d)x^2+(-a-c+3d)x\\ +(a-b-d)\end{array}$$$$1)a+c=0$$$$2)-a+b-3c+d=0$$$$3)3c-3d=10$$$$4)-a-c+3d=-8$$$$5)a-b-d=1$$$$1\Rightarrow c=-a$$$$\Rightarrow \{\begin{array}{l}b+d=-2a\\ -3a-3d=10\Rightarrow d=-\frac{3a+10}{3}\\ d=\frac{-8}{3}\end{array}$$$$\Rightarrow \{\begin{array}{l}b=-2a+\frac{8}{3}\\ 3a+10=8\Rightarrow a=6\Rightarrow c=-6\end{array}$$$$\Rightarrow b=-12+\frac{8}{3}=\frac{-36+8}{3}=\frac{-28}{3}$$$$\frac{10x^2-8x+1}{{(x-1)}^2(x^2+x+1)}=\frac{6}{(x-1)}-\frac{28}{3{(x-1)}^2}-\frac{18x+8}{3(x^2+x+1)}$$$$\int \frac{10x^2-8x+1}{x^4-x^3-x+1}dx$$$$=6\int \frac{dx}{x-1}-\frac{28}{3}\int \frac{dx}{{(x-1)}^2}-\frac{1}{3}\int \frac{18x+9-1}{x^2+x+1}dx$$$$=6log\mid x-1\mid +\frac{28}{3(x-1)}-\frac{9}{3}log\mid x^2+x+1\mid +\frac{1}{3}\int \frac{dx}{{(x+\frac{1}{2})}^2+\frac{3}{4}}$$$$=6log\mid x-1\mid +\frac{28}{3(x-1)}-3log\mid x^2+x+1\mid +\frac{1}{3}\int \frac{dx}{{(x+\frac{1}{2})}^2+{\left(\frac{\sqrt{3}}{2}\right)}^2}$$$$=6log\mid x-1\mid +\frac{28}{3(x-1)}-3log\mid x^2+x+1\mid +\frac{1}{3}\times \frac{2}{\sqrt{3}}{tan}^{-1}\left(\frac{x+\frac{1}{2}}{\frac{\sqrt{3}}{2}}\right)+C$$$$=6log\mid x-1\mid +\frac{28}{3(x-1)}-3log\mid x^2+x+1\mid +\frac{2}{3\sqrt{3}}{tan}^{-1}\left(\frac{2x+1}{\sqrt{3}}\right)+C$$

Commented by Kunal12588 last updated on 08/Jan/20

$$nexttimetryyourselffirst!$$

Commented by key of knowledge last updated on 08/Jan/20

$$\log \mathrm{is}\mathrm{not},\ln \mathrm{is}\mathrm{true}(\int \frac{\mathrm{du}}{\mathrm{u}}=\mathrm{lnx})$$

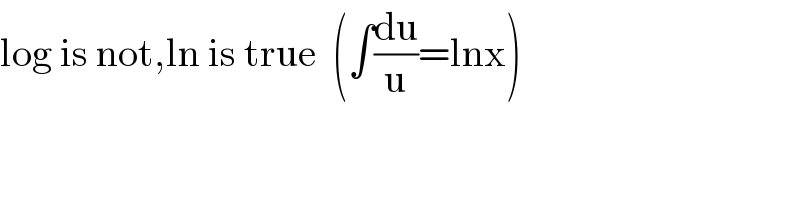
Commented by kaivan.ahmadi last updated on 08/Jan/20

$$thankusir$$

Commented by MJS last updated on 08/Jan/20

$$\mathrm{some}\mathrm{write}\log \mathrm{for}\ln ,\mathrm{and}{\log }_{10}$$$$\mathrm{others}\mathrm{write}\log \mathrm{for}{\log }_{10}\mathrm{and}\ln$$$$\mathrm{in}\mathrm{case}\mathrm{of}\mathrm{integrals}\mathrm{there}\mathrm{had}\mathrm{been}\mathrm{no}\mathrm{case}$$$$\mathrm{yet}\mathrm{where}\log \mathrm{meant}{\log }_{10}$$

Commented by mathmax by abdo last updated on 08/Jan/20

$$bynotationLogmeanslnandlogmeans{log}_{10}...$$

Commented by Kunal12588 last updated on 09/Jan/20

$$yeah,thereismuchofconfusion$$$$butIamjustfollowingwhatIlearnedin$$$$myschoolandNCERTbook.$$$$loga\to {log}_{e}aandforreferringto{log}_{10}a$$$$wewriteitlikethat{log}_{10}a.$$$$nothingmentionedaboutln.$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com