
Previous in Probability and Statistics Next in Probability and Statistics
Question Number 77777 by jagoll last updated on 10/Jan/20

$${The}\:{number} \\ $$$${of}\:{words}\:{can}\:{be}\:{made}\:{formed} \\ $$$${using}\:{all}\:{letters}\:{in}\:{the}\:{word} \\ $$$$'{amutasia}'\:{by}\:{not}\:{containing} \\ $$$${the}\:{three}\:{vowels}\:{side}\:{by}\:{side}\:{is}\:? \\ $$
Answered by mr W last updated on 10/Jan/20

$${AMUTASIA}\:{contains} \\ $$$$\mathrm{3}×\:{A} \\ $$$$\mathrm{1}×\:{I} \\ $$$$\mathrm{1}×\:{U} \\ $$$$\mathrm{1}×\:{M} \\ $$$$\mathrm{1}×\:{S} \\ $$$$\mathrm{1}×\:{T} \\ $$$${totally}\:\mathrm{8}\:{letters} \\ $$$$ \\ $$$${total}\:{number}\:{of}\:{words}\:{formed}\:{using} \\ $$$${all}\:{letters}: \\ $$$$\frac{\mathrm{8}!}{\mathrm{3}!}=\mathrm{6720} \\ $$$${among}\:{them}\:{number}\:{of}\:{words}\:{containing} \\ $$$${the}\:{three}\:{vowels}\:{side}\:{by}\:{side}: \\ $$$$\frac{\mathrm{3}×\mathrm{6}!\mathrm{3}!}{\mathrm{2}!}=\mathrm{6480} \\ $$$$ \\ $$$$\Rightarrow{requested}\:{number}:\:\mathrm{6720}−\mathrm{6480}=\mathrm{240} \\ $$
Commented by jagoll last updated on 10/Jan/20
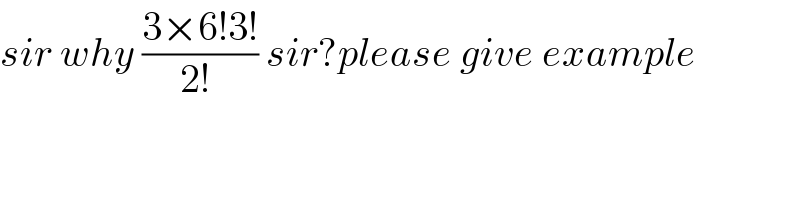
$${sir}\:{why}\:\frac{\mathrm{3}×\mathrm{6}!\mathrm{3}!}{\mathrm{2}!\:}\:{sir}?{please}\:{give}\:{example} \\ $$
Commented by mr W last updated on 10/Jan/20

$${in}\:{fact}\:{the}\:{question}\:{is}\:{not}\:{exact}. \\ $$$${the}\:{three}\:{vowols}\:{should}\:{not}\:{be}\:{side}\:{by}\:{side}. \\ $$$${but}\:{are}\:{SIAAUMAT}\:{and}\:{SIAAAUMT} \\ $$$${valid}?\:{for}\:{me}\:{they}\:{are}\:{valid}.\:{side}\:{by} \\ $$$${side}\:{means}\:{for}\:{me}\:{IAU},\:{but}\:{not}\:{IAAU}. \\ $$
Commented by jagoll last updated on 10/Jan/20

$${valid}\:{sir} \\ $$
Commented by mr W last updated on 10/Jan/20

$${then}\:{the}\:{answer}\:{is}\:\mathrm{240}.\:{is}\:{this}\:{correct}? \\ $$
Commented by jagoll last updated on 10/Jan/20

$${the}\:{problem}\:{is}\:{not}\:{multiple}\: \\ $$$${choice}\:{sir}.\:{i}\:{still}\:{don}'{t}\: \\ $$$${understand}\:{the}\:{formula} \\ $$$${reduction}\:\frac{\mathrm{3}×\mathrm{6}!\mathrm{3}!}{\mathrm{2}!\:}\: \\ $$
Commented by jagoll last updated on 10/Jan/20
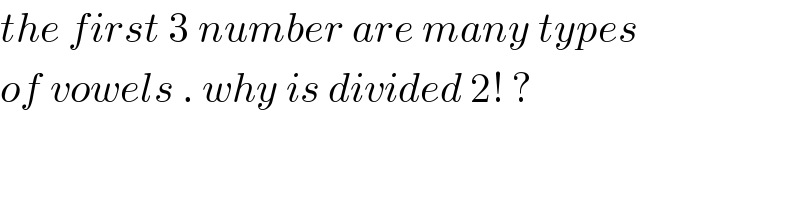
$${the}\:{first}\:\mathrm{3}\:{number}\:{are}\:{many}\:{types} \\ $$$${of}\:{vowels}\:.\:{why}\:{is}\:{divided}\:\mathrm{2}!\:? \\ $$
Commented by malwaan last updated on 10/Jan/20
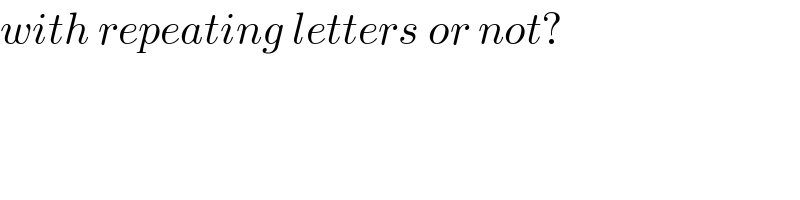
$${with}\:{repeating}\:{letters}\:{or}\:{not}? \\ $$
Commented by jagoll last updated on 10/Jan/20

$${not}\:{sir} \\ $$
Commented by mr W last updated on 10/Jan/20
![to jagoll sir: image you mark the three letters A with a pen as A_1 ,A_2 ,A_3 and treat them as different letters. certainly they are in fact identical. then we select three vowols, e.g. A_1 ,I,U, as a group, say [A_1 IU], as if they were a single letter. then we arrange the 6 “letters”: [A_1 IU],A_2 ,A_3 ,M,S,T. there are 6! ways to arrange them. but A_2 and A_3 are in fact identical, therefore there are in fact only ((6!)/(2!)) different ways. on the other side, we can arrange the three vowols A_1 ,I,U inside the group in 3! ways. therefore we have totally ((6!3!)/(2!)) ways when we take A_1 as vowol. since we can also select A_2 or A_3 as vowol, the number of all possibilties is ((3×6!3!)/(2!)). clear?](Q77797.png)
$${to}\:{jagoll}\:{sir}: \\ $$$${image}\:{you}\:{mark}\:{the}\:{three}\:{letters}\:{A}\:{with} \\ $$$${a}\:{pen}\:{as}\:{A}_{\mathrm{1}} ,{A}_{\mathrm{2}} ,{A}_{\mathrm{3}} \:{and}\:{treat}\:{them}\:{as} \\ $$$${different}\:{letters}.\:{certainly}\:{they}\:{are} \\ $$$${in}\:{fact}\:{identical}. \\ $$$${then}\:{we}\:{select}\:{three}\:{vowols},\:{e}.{g}.\:{A}_{\mathrm{1}} ,{I},{U}, \\ $$$${as}\:{a}\:{group},\:{say}\:\left[{A}_{\mathrm{1}} {IU}\right],\:{as}\:{if}\:{they}\:{were}\: \\ $$$${a}\:{single}\:{letter}.\:{then}\:{we}\:{arrange}\:{the} \\ $$$$\mathrm{6}\:``{letters}'':\:\left[{A}_{\mathrm{1}} {IU}\right],{A}_{\mathrm{2}} ,{A}_{\mathrm{3}} ,{M},{S},{T}. \\ $$$${there}\:{are}\:\mathrm{6}!\:{ways}\:{to}\:{arrange}\:{them}. \\ $$$${but}\:{A}_{\mathrm{2}} \:{and}\:{A}_{\mathrm{3}} \:{are}\:{in}\:{fact}\:{identical}, \\ $$$${therefore}\:{there}\:{are}\:{in}\:{fact}\:{only} \\ $$$$\frac{\mathrm{6}!}{\mathrm{2}!}\:{different}\:{ways}.\:{on}\:{the}\:{other}\:{side}, \\ $$$${we}\:{can}\:{arrange}\:{the}\:{three}\:{vowols}\:{A}_{\mathrm{1}} ,{I},{U} \\ $$$${inside}\:{the}\:{group}\:{in}\:\mathrm{3}!\:{ways}.\:{therefore}\:{we}\:{have} \\ $$$${totally}\:\frac{\mathrm{6}!\mathrm{3}!}{\mathrm{2}!}\:{ways}\:{when}\:{we}\:{take}\:{A}_{\mathrm{1}} \:{as} \\ $$$${vowol}.\:{since}\:{we}\:{can}\:{also}\:{select}\:{A}_{\mathrm{2}} \:{or} \\ $$$${A}_{\mathrm{3}} \:{as}\:{vowol},\:{the}\:{number}\:{of}\:{all}\:{possibilties} \\ $$$${is}\:\frac{\mathrm{3}×\mathrm{6}!\mathrm{3}!}{\mathrm{2}!}. \\ $$$${clear}? \\ $$
Commented by jagoll last updated on 10/Jan/20
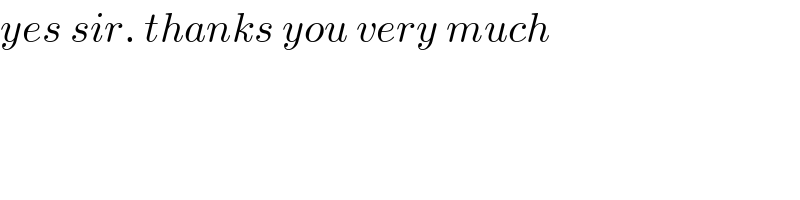
$${yes}\:{sir}.\:{thanks}\:{you}\:{very}\:{much} \\ $$
Commented by malwaan last updated on 10/Jan/20
$$\boldsymbol{{great}}\:\boldsymbol{{sir}}\:\boldsymbol{{Mr}}\:\boldsymbol{{W}} \\ $$$$\boldsymbol{{thank}}\:\boldsymbol{{you}}\:\boldsymbol{{very}}\:\boldsymbol{{much}} \\ $$$$ \\ $$
