
Question and Answers Forum
Question Number 77842 by jagoll last updated on 11/Jan/20
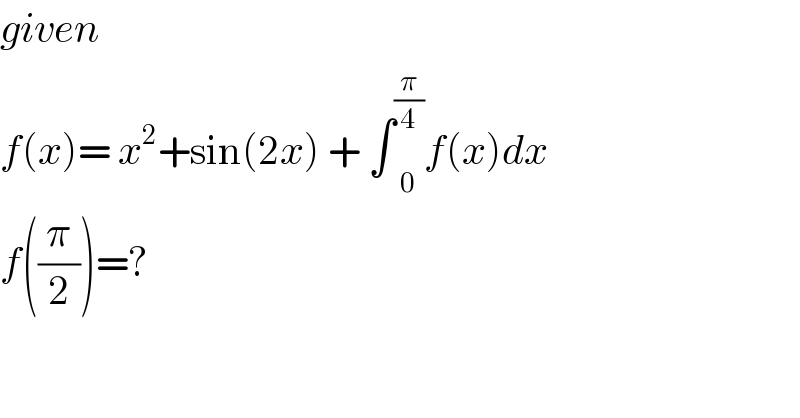
Answered by mr W last updated on 11/Jan/20
![let ∫_0 ^(π/4) f(x)dx=a=constant f(x)= x^2 +sin(2x)+a ∫_0 ^(π/4) f(x)dx=[(x^3 /3)−((cos (2x))/2)+ax]_0 ^(π/4) =a (π^3 /(192))+(1/2)+((aπ)/4)=a ⇒a=((π^3 +96)/(48(4−π))) f(x)= x^2 +sin(2x)+((π^3 +96)/(48(4−π))) f((π/2))= (π^2 /4)+((π^3 +96)/(48(4−π)))=(((48−11π)π^2 +96)/(48(4−π)))](Q77844.png)
Commented by jagoll last updated on 11/Jan/20

| ||
Question and Answers Forum | ||
Question Number 77842 by jagoll last updated on 11/Jan/20 | ||
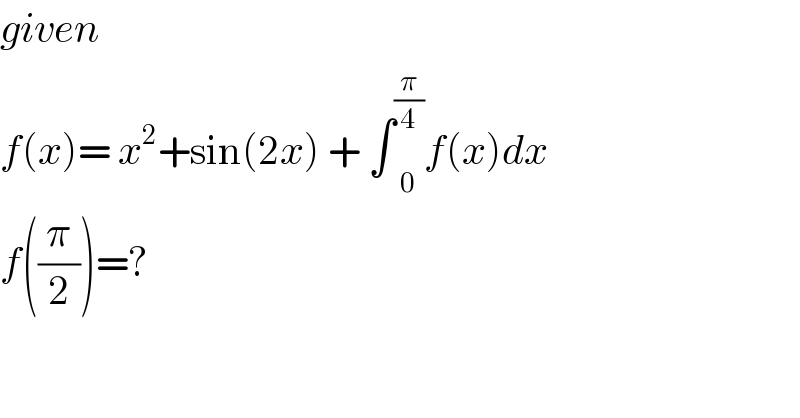 | ||
Answered by mr W last updated on 11/Jan/20 | ||
![let ∫_0 ^(π/4) f(x)dx=a=constant f(x)= x^2 +sin(2x)+a ∫_0 ^(π/4) f(x)dx=[(x^3 /3)−((cos (2x))/2)+ax]_0 ^(π/4) =a (π^3 /(192))+(1/2)+((aπ)/4)=a ⇒a=((π^3 +96)/(48(4−π))) f(x)= x^2 +sin(2x)+((π^3 +96)/(48(4−π))) f((π/2))= (π^2 /4)+((π^3 +96)/(48(4−π)))=(((48−11π)π^2 +96)/(48(4−π)))](Q77844.png) | ||
| ||
Commented by jagoll last updated on 11/Jan/20 | ||
 | ||