Question Number 78021 by jagoll last updated on 13/Jan/20
![lim_(x→0) (1/x^2 )[∫^(x^2 +(π/3)) _(π/3) ((cos x)/x) dx ] =](Q78021.png)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\left[\underset{\frac{\pi}{\mathrm{3}}} {\int}^{{x}^{\mathrm{2}} +\frac{\pi}{\mathrm{3}}} \frac{\mathrm{cos}\:{x}}{{x}}\:{dx}\:\right]\:= \\ $$
Commented by mr W last updated on 13/Jan/20
![lim_(x→0) (1/x^2 )[∫^(x^2 +(π/3)) _(π/3) ((cos x)/x) dx ] =lim_(x→0) ((((cos (x^2 +(π/3)))/(x^2 +(π/3)))×2x)/(2x)) =lim_(x→0) ((cos (x^2 +(π/3)))/(x^2 +(π/3))) =(3/π)×(1/2)=(3/(2π))](Q78022.png)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\left[\underset{\frac{\pi}{\mathrm{3}}} {\int}^{{x}^{\mathrm{2}} +\frac{\pi}{\mathrm{3}}} \frac{\mathrm{cos}\:{x}}{{x}}\:{dx}\:\right] \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{cos}\:\left({x}^{\mathrm{2}} +\frac{\pi}{\mathrm{3}}\right)}{{x}^{\mathrm{2}} +\frac{\pi}{\mathrm{3}}}×\mathrm{2}{x}}{\mathrm{2}{x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:\left({x}^{\mathrm{2}} +\frac{\pi}{\mathrm{3}}\right)}{{x}^{\mathrm{2}} +\frac{\pi}{\mathrm{3}}} \\ $$$$=\frac{\mathrm{3}}{\pi}×\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{2}\pi} \\ $$
Commented by jagoll last updated on 13/Jan/20
$${by}\:{using}\:{fundamental}\:{calculus}\:{theorem} \\ $$$${sir}?\:{thanks}\: \\ $$
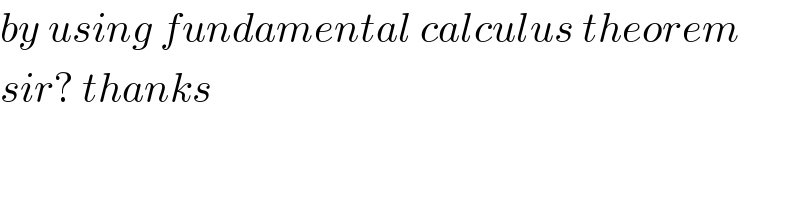
Commented by mr W last updated on 13/Jan/20
$${i}\:{don}'{t}\:{know}\:{what}\:{is}\:``{fundamental} \\ $$$${calculus}\:{theorem}''. \\ $$
Commented by jagoll last updated on 13/Jan/20
![(d/dx)[∫_0 ^x f(u)du] = f(x) sir](Q78028.png)
$$\frac{{d}}{{dx}}\left[\underset{\mathrm{0}} {\overset{{x}} {\int}}\:{f}\left({u}\right){du}\right]\:=\:{f}\left({x}\right)\:{sir} \\ $$
Commented by mr W last updated on 13/Jan/20
![generally: (d/dx)[∫_(h(x)) ^(g(x)) f(u)du] = f(g(x))g′(x)−f(h(x))h′(x)](Q78032.png)
$${generally}: \\ $$$$\frac{{d}}{{dx}}\left[\underset{{h}\left({x}\right)} {\overset{{g}\left({x}\right)} {\int}}\:{f}\left({u}\right){du}\right]\:=\:{f}\left({g}\left({x}\right)\right){g}'\left({x}\right)−{f}\left({h}\left({x}\right)\right){h}'\left({x}\right) \\ $$
Commented by jagoll last updated on 13/Jan/20
$${okay}\:{sir}\:{thank}\:{you} \\ $$
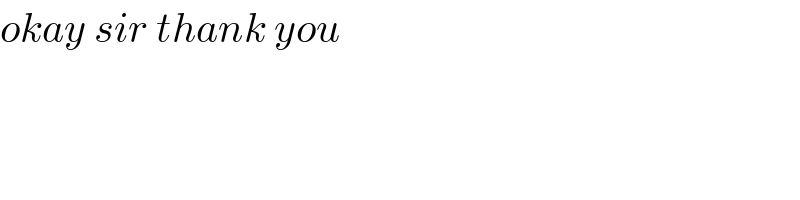
Commented by msup trace by abdo last updated on 13/Jan/20
,x^2 +(π/3)[ / A(x)=(1/c) ∫_(π/3) ^(x^2 +(π/3)) cost dt =(1/c)(sin(x^2 +(π/3))−((√3)/2)) ⇒((A(x))/x^2 ) =((sin(x^2 +(π/3))−((√3)/2))/(cx^2 )) =(((1/2)sin(x^2 )+((√3)/2)cos(x^2 )−((√3)/2))/(cx^2 )) ∼(1/(2cx^2 )){x^2 +(√3)(1−(x^4 /2))−(√3)} =(1/(2c))−(x^2 /(4c)) ⇒lim_(x→0) A(x) =(1/(2×(π/3))) =(3/(2π)) .](Q78035.png)
$${let}\:{A}\left({x}\right)=\int_{\frac{\pi}{\mathrm{3}}} ^{{x}^{\mathrm{2}} +\frac{\pi}{\mathrm{3}}} \:\frac{{cost}}{{t}}{dt} \\ $$$$\left.\exists\:{c}\:\in\right]\frac{\pi}{\mathrm{3}},{x}^{\mathrm{2}} +\frac{\pi}{\mathrm{3}}\left[\:/\right. \\ $$$${A}\left({x}\right)=\frac{\mathrm{1}}{{c}}\:\int_{\frac{\pi}{\mathrm{3}}} ^{{x}^{\mathrm{2}} \:+\frac{\pi}{\mathrm{3}}} {cost}\:{dt} \\ $$$$=\frac{\mathrm{1}}{{c}}\left({sin}\left({x}^{\mathrm{2}} +\frac{\pi}{\mathrm{3}}\right)−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$$\Rightarrow\frac{{A}\left({x}\right)}{{x}^{\mathrm{2}} }\:=\frac{{sin}\left({x}^{\mathrm{2}} +\frac{\pi}{\mathrm{3}}\right)−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}{{cx}^{\mathrm{2}} } \\ $$$$=\frac{\frac{\mathrm{1}}{\mathrm{2}}{sin}\left({x}^{\mathrm{2}} \right)+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{cos}\left({x}^{\mathrm{2}} \right)−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}{{cx}^{\mathrm{2}} } \\ $$$$\sim\frac{\mathrm{1}}{\mathrm{2}{cx}^{\mathrm{2}} }\left\{{x}^{\mathrm{2}} +\sqrt{\mathrm{3}}\left(\mathrm{1}−\frac{{x}^{\mathrm{4}} }{\mathrm{2}}\right)−\sqrt{\mathrm{3}}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{c}}−\frac{{x}^{\mathrm{2}} }{\mathrm{4}{c}}\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \:{A}\left({x}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}×\frac{\pi}{\mathrm{3}}}\:=\frac{\mathrm{3}}{\mathrm{2}\pi}\:. \\ $$$$ \\ $$