
Question Number 78049 by Pratah last updated on 13/Jan/20

Commented by Pratah last updated on 14/Jan/20

$$? \\ $$
Answered by behi83417@gmail.com last updated on 14/Jan/20

$$\mathrm{for}:\mathrm{n}=\mathrm{1}\Rightarrow\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}_{\mathrm{1}} }}−\frac{\mathrm{1}}{\mathrm{a}_{\mathrm{1}} }=\mathrm{1}+\mathrm{a}_{\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{a}_{\mathrm{1}} }\geqslant\mathrm{1}\left(\mathrm{a}_{\mathrm{1}} \in\mathrm{N}\right) \\ $$$$\mathrm{for}:\mathrm{n}=\mathrm{2}\Rightarrow\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}_{\mathrm{1}} }}+\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}_{\mathrm{1}} }}−\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{a}_{\mathrm{1}} }+\frac{\mathrm{1}}{\mathrm{a}_{\mathrm{2}} }}= \\ $$$$=\mathrm{2}+\mathrm{a}_{\mathrm{1}} +\mathrm{a}_{\mathrm{2}} −\frac{\mathrm{a}_{\mathrm{1}} .\mathrm{a}_{\mathrm{2}} }{\mathrm{a}_{\mathrm{1}} +\mathrm{a}_{\mathrm{2}} }\geqslant\mathrm{2}+\mathrm{a}_{\mathrm{1}} +\mathrm{a}_{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}>\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{a}_{\mathrm{i}} \in\mathrm{N}\right) \\ $$$$\mathrm{it}\:\mathrm{is}\:\mathrm{true}\:\mathrm{for}:\mathrm{n}=\mathrm{1},\mathrm{2}.\mathrm{let}\:\mathrm{assume}\:\mathrm{that}\:\mathrm{is} \\ $$$$\mathrm{true}\:\mathrm{for}:\mathrm{n}=\mathrm{k}\in\mathrm{N}.\mathrm{now}\:\mathrm{we}\:\mathrm{show}\:\mathrm{that}\:\mathrm{it}\:\mathrm{is} \\ $$$$\mathrm{true}\:\mathrm{for}:\mathrm{n}=\mathrm{k}+\mathrm{1} \\ $$$$\mathrm{n}=\mathrm{k}+\mathrm{1}\Rightarrow\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}_{\mathrm{1}} }}+\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}_{\mathrm{2}} }}+..+\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}_{\mathrm{k}+\mathrm{1}} }}− \\ $$$$−\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{a}_{\mathrm{1}} }+\frac{\mathrm{1}}{\mathrm{a}_{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{a}_{\mathrm{3}} }+.....+\frac{\mathrm{1}}{\mathrm{a}_{\mathrm{k}+\mathrm{1}} }}\geqslant\frac{\mathrm{1}}{\mathrm{n}}+\mathrm{1}+\mathrm{a}_{\mathrm{k}+\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}} \\ $$$$=\mathrm{1}+\mathrm{a}_{\mathrm{k}+\mathrm{1}} +\frac{\mathrm{1}}{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}>\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\:\:\:\:.\blacksquare \\ $$
Commented by mr W last updated on 14/Jan/20

$${great}! \\ $$$${i}\:{think}\:{the}\:{inequality}\:{is}\:{even}\:{valid}, \\ $$$${if}\:{a}_{{i}} \:{are}\:{not}\:{positive}\:{intergers},\:{but} \\ $$$${any}\:{positive}\:{real}\:{numbers}. \\ $$
Answered by mr W last updated on 14/Jan/20
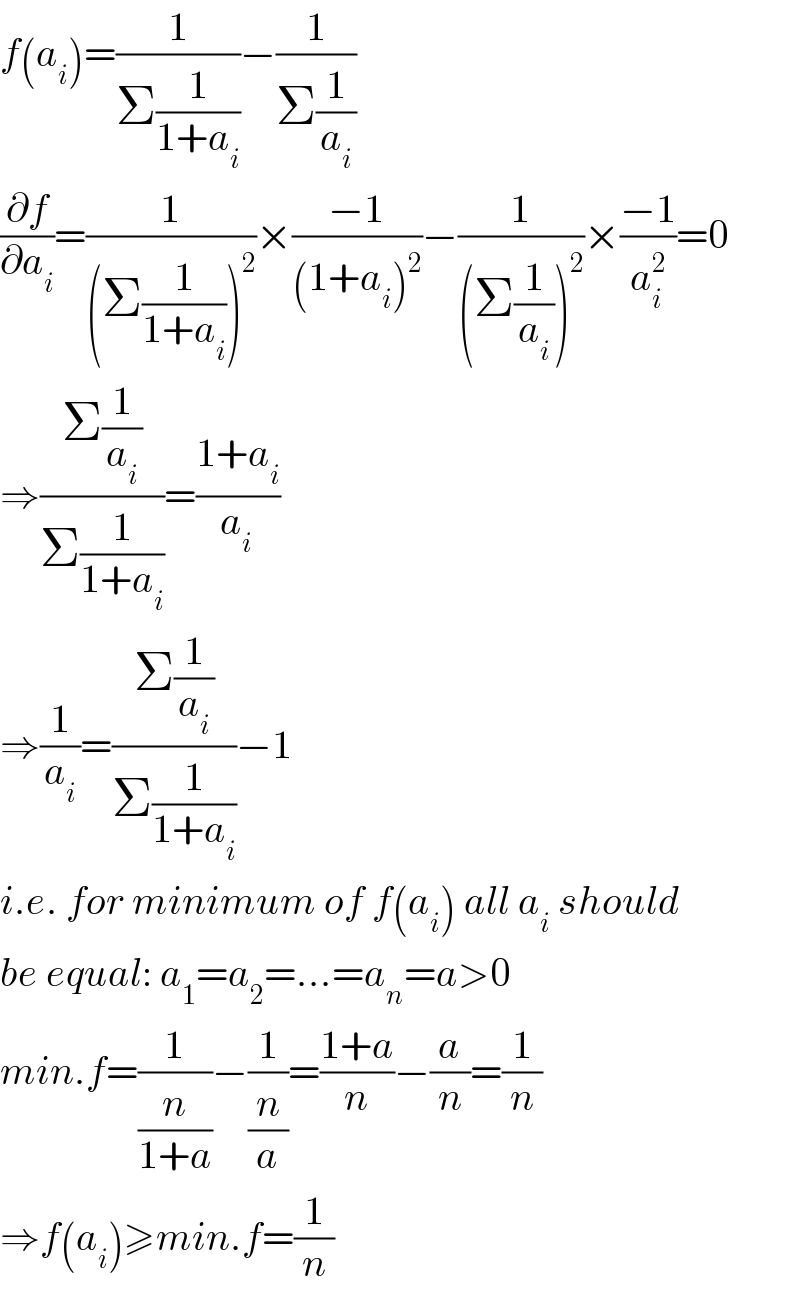
$${f}\left({a}_{{i}} \right)=\frac{\mathrm{1}}{\Sigma\frac{\mathrm{1}}{\mathrm{1}+{a}_{{i}} }}−\frac{\mathrm{1}}{\Sigma\frac{\mathrm{1}}{{a}_{{i}} }} \\ $$$$\frac{\partial{f}}{\partial{a}_{{i}} }=\frac{\mathrm{1}}{\left(\Sigma\frac{\mathrm{1}}{\mathrm{1}+{a}_{{i}} }\right)^{\mathrm{2}} }×\frac{−\mathrm{1}}{\left(\mathrm{1}+{a}_{{i}} \right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\left(\Sigma\frac{\mathrm{1}}{{a}_{{i}} }\right)^{\mathrm{2}} }×\frac{−\mathrm{1}}{{a}_{{i}} ^{\mathrm{2}} }=\mathrm{0} \\ $$$$\Rightarrow\frac{\Sigma\frac{\mathrm{1}}{{a}_{{i}} }}{\Sigma\frac{\mathrm{1}}{\mathrm{1}+{a}_{{i}} }}=\frac{\mathrm{1}+{a}_{{i}} }{{a}_{{i}\:} } \\ $$$$\Rightarrow\frac{\mathrm{1}}{{a}_{{i}} }=\frac{\Sigma\frac{\mathrm{1}}{{a}_{{i}} }}{\Sigma\frac{\mathrm{1}}{\mathrm{1}+{a}_{{i}} }}−\mathrm{1} \\ $$$${i}.{e}.\:{for}\:{minimum}\:{of}\:{f}\left({a}_{{i}} \right)\:{all}\:{a}_{{i}} \:{should} \\ $$$${be}\:{equal}:\:{a}_{\mathrm{1}} ={a}_{\mathrm{2}} =...={a}_{{n}} ={a}>\mathrm{0} \\ $$$${min}.{f}=\frac{\mathrm{1}}{\frac{{n}}{\mathrm{1}+{a}}}−\frac{\mathrm{1}}{\frac{{n}}{{a}}}=\frac{\mathrm{1}+{a}}{{n}}−\frac{{a}}{{n}}=\frac{\mathrm{1}}{{n}} \\ $$$$\Rightarrow{f}\left({a}_{{i}} \right)\geqslant{min}.{f}=\frac{\mathrm{1}}{{n}} \\ $$
Commented by mr W last updated on 14/Jan/20
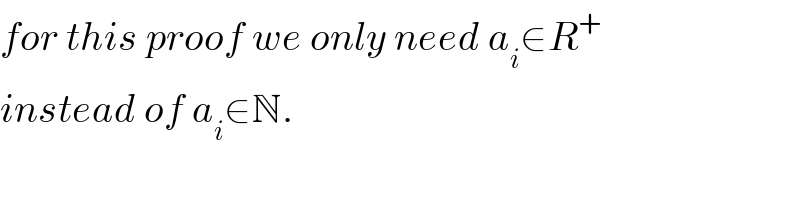
$${for}\:{this}\:{proof}\:{we}\:{only}\:{need}\:{a}_{{i}} \in{R}^{+} \\ $$$${instead}\:{of}\:{a}_{{i}} \in\mathbb{N}. \\ $$
