
Question Number 78074 by Rio Michael last updated on 14/Jan/20
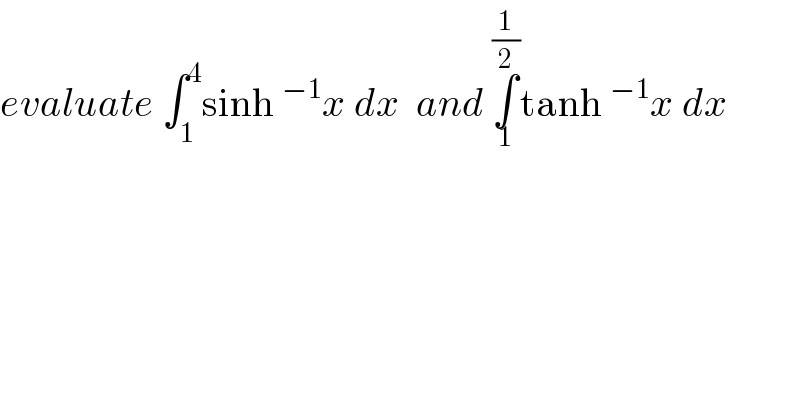
$${evaluate}\:\int_{\mathrm{1}} ^{\mathrm{4}} \mathrm{sinh}\:^{−\mathrm{1}} {x}\:{dx}\:\:{and}\:\underset{\mathrm{1}} {\overset{\frac{\mathrm{1}}{\mathrm{2}}} {\int}}\mathrm{tanh}\:^{−\mathrm{1}} {x}\:{dx} \\ $$
Answered by mr W last updated on 14/Jan/20
![∫sinh^(−1) x dx =∫ln (x+(√(1+x^2 ))) dx =xln (x+(√(1+x^2 )))−∫((x(1+(x/(√(1+x^2 )))))/(x+(√(1+x^2 )))) dx =xln (x+(√(1+x^2 )))−∫(x/(√(1+x^2 ))) dx =xln (x+(√(1+x^2 )))−∫(1/(2(√(1+x^2 )))) d(1+x^2 ) =xln (x+(√(1+x^2 )))−(√(1+x^2 ))+C ∫_1 ^4 sinh^(−1) x dx =[xln (x+(√(1+x^2 )))−(√(1+x^2 ))]_1 ^4 =4ln (4+(√(17)))−ln (1+(√2))−(√(17))+(√2)](Q78133.png)
$$\int\mathrm{sinh}^{−\mathrm{1}} \:{x}\:{dx} \\ $$$$=\int\mathrm{ln}\:\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)\:{dx} \\ $$$$={x}\mathrm{ln}\:\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)−\int\frac{{x}\left(\mathrm{1}+\frac{{x}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right)}{{x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:{dx} \\ $$$$={x}\mathrm{ln}\:\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)−\int\frac{{x}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:{dx} \\ $$$$={x}\mathrm{ln}\:\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)−\int\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:{d}\left(\mathrm{1}+{x}^{\mathrm{2}} \right) \\ $$$$={x}\mathrm{ln}\:\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }+{C} \\ $$$$ \\ $$$$\int_{\mathrm{1}} ^{\mathrm{4}} \mathrm{sinh}^{−\mathrm{1}} \:{x}\:{dx} \\ $$$$=\left[{x}\mathrm{ln}\:\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right]_{\mathrm{1}} ^{\mathrm{4}} \\ $$$$=\mathrm{4ln}\:\left(\mathrm{4}+\sqrt{\mathrm{17}}\right)−\mathrm{ln}\:\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)−\sqrt{\mathrm{17}}+\sqrt{\mathrm{2}} \\ $$
Answered by mr W last updated on 14/Jan/20
![∫tanh^(−1) x dx =(1/2)∫ln ((1+x)/(1−x)) dx =(1/2)[xln ((1−x)/(1+x))+∫((2x)/(1−x^2 )) dx] =(1/2)[xln ((1−x)/(1+x))−∫(1/(1−x^2 )) d(1−x^2 )] =(1/2)[xln ((1−x)/(1+x))−ln (1−x^2 )]+C](Q78137.png)
$$\int\mathrm{tanh}^{−\mathrm{1}} \:{x}\:{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{ln}\:\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\:{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[{x}\mathrm{ln}\:\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}+\int\frac{\mathrm{2}{x}}{\mathrm{1}−{x}^{\mathrm{2}} }\:{dx}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[{x}\mathrm{ln}\:\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}−\int\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }\:{d}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[{x}\mathrm{ln}\:\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}−\mathrm{ln}\:\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\right]+{C} \\ $$
