
Question and Answers Forum
Question Number 78119 by jagoll last updated on 14/Jan/20
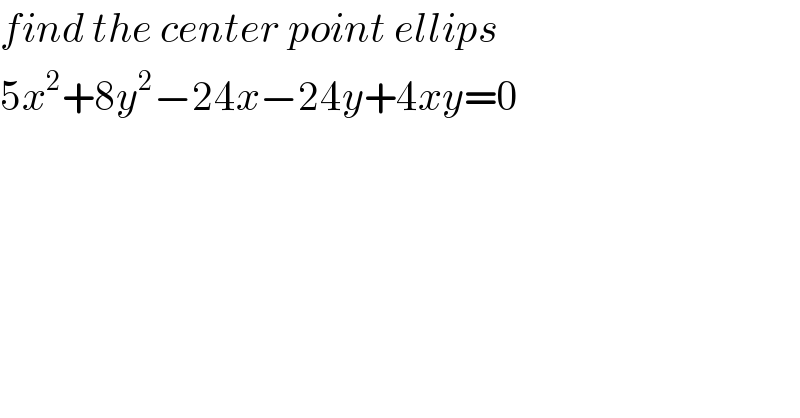
Commented by jagoll last updated on 14/Jan/20
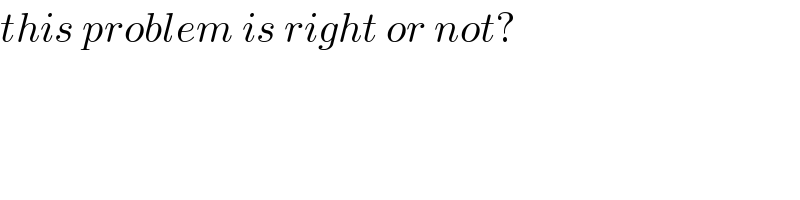
Commented by mr W last updated on 14/Jan/20
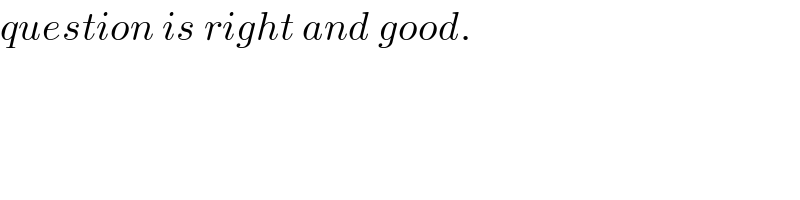
Commented by MJS last updated on 14/Jan/20
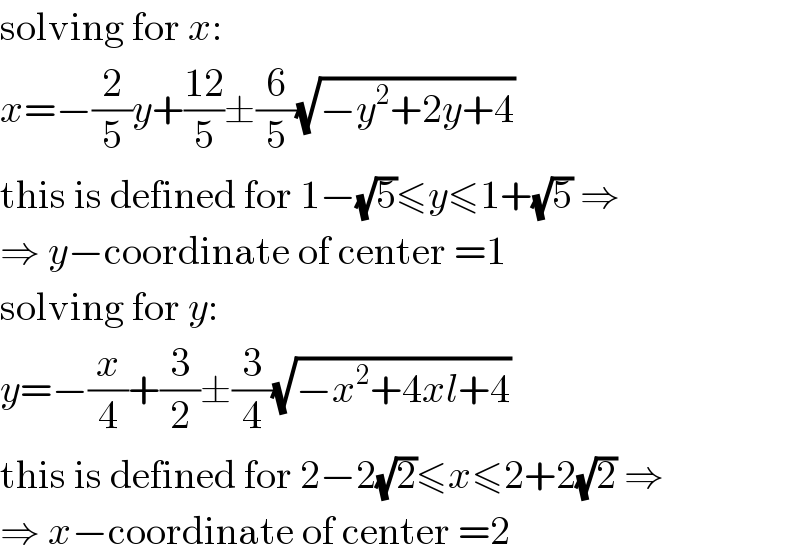
Commented by jagoll last updated on 14/Jan/20

Commented by jagoll last updated on 14/Jan/20
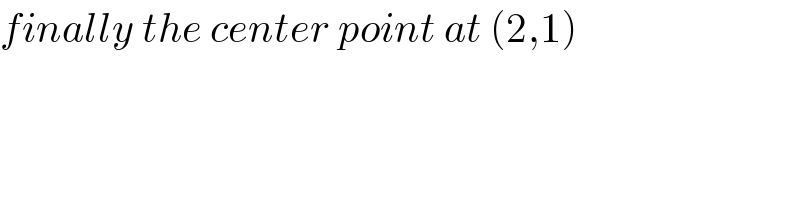
Commented by MJS last updated on 14/Jan/20

Answered by mr W last updated on 15/Jan/20
![if you don′t like to learn too many formulas, you can determine the parameters of the ellipse in following way: step 1: determine center point that means to determine the range of x and y ordinates. (see also sir MJS′ post) we form eqn. as quadratic eqn. w.r.t. y: 8y^2 +4(x−6)y+5x^2 −24x=0 Δ=4^2 (x−6)^2 −4×8×(5x^2 −24x)≥0 (x−6)^2 −2(5x^2 −24x)≥0 −x^2 +4x+4≥0 x^2 −4x−4≤0 (x−2)^2 −8≤0 ⇒2−2(√2)≤x≤2+2(√2) ⇒x_C =2 we form eqn. as quadratic eqn. w.r.t. x: 5x^2 +4(y−6)x+8y^2 −24y=0 Δ=4^2 (y−6)^2 −4×5(8y^2 −24y)≥0 (y−6)^2 −5(2y^2 −6y)≥0 −y^2 +2y+4≥0 y^2 −2y−4≤0 (y−1)^2 −5≤0 ⇒1−(√5)≤y≤1+(√5) ⇒y_C =1 ⇒center point of ellipse is C(2,1) step 2: make the center point as origin replace x with x+x_C and y with y+y_C in the eqn. 5(x+2)^2 +8(y+1)^2 −24(x+2)−24(y+1)+4(x+2)(y+1)=0 ⇒5x^2 +8y^2 +4xy−36=0 step 3: find the major and minor axis express the eqn. in polar form with x=r cos θ, y=r sin θ 5r^2 cos^2 θ+8r^2 sin^2 θ+4r^2 sin θcos θ−36=0 [(5/2)(cos 2θ+1)+4(1−cos 2θ)+2sin 2θ]r^2 −36=0 (13−3cos 2θ+4sin 2θ)r^2 =72 [13+5(−(3/5)cos 2θ+(4/5)sin 2θ)]r^2 =72 [13+5(−sin αcos 2θ+cos αsin 2θ)]r^2 =72 [13+5 sin (2θ−α)]r^2 =72 ⇒r=((6(√2))/(√(13+5 sin (2θ−α)))) r_(max) =major axis=a=((6(√2))/(√(13−5)))=3 at 2θ−α=−(π/2) or θ=tan^(−1) (1/3)−(π/4) r_(min) =minor axis=b=((6(√2))/(√(13+5)))=2 at 2θ−α=(π/2) or θ=tan^(−1) (1/3)+(π/4) we know in this way also that the ellipse is rotated by angle tan^(−1) (1/3)−(π/4)](Q78228.png)
Commented by mr W last updated on 15/Jan/20

