Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 78177 by jagoll last updated on 15/Jan/20

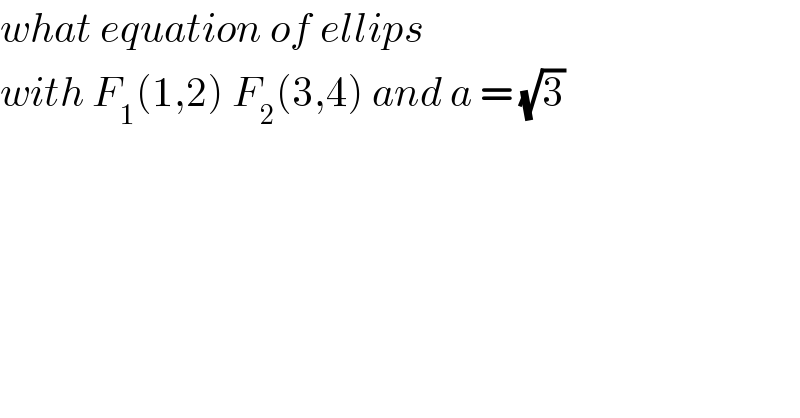
what equation of ellips with F_1 (1,2) F_2 (3,4) and a = (√3)

$${what}\:{equation}\:{of}\:{ellips} \\ $$$${with}\:{F}_{\mathrm{1}} \left(\mathrm{1},\mathrm{2}\right)\:{F}_{\mathrm{2}} \left(\mathrm{3},\mathrm{4}\right)\:{and}\:{a}\:=\:\sqrt{\mathrm{3}} \\ $$

Commented by MJS last updated on 15/Jan/20

what are we “allowed to do”?

$$\mathrm{what}\:\mathrm{are}\:\mathrm{we}\:``\mathrm{allowed}\:\mathrm{to}\:\mathrm{do}''? \\ $$

Commented by jagoll last updated on 15/Jan/20

yes sir i can′t solve this problem

$${yes}\:{sir}\:{i}\:{can}'{t}\:{solve}\:{this}\:{problem} \\ $$

Commented by jagoll last updated on 15/Jan/20

what is center point at (((1+3)/2), ((2+4)/2))= (2,3) sir?

$${what}\:{is}\:{center}\:{point}\:{at}\:\left(\frac{\mathrm{1}+\mathrm{3}}{\mathrm{2}},\:\frac{\mathrm{2}+\mathrm{4}}{\mathrm{2}}\right)=\:\left(\mathrm{2},\mathrm{3}\right)\:{sir}? \\ $$

Commented by jagoll last updated on 15/Jan/20

Commented by MJS last updated on 15/Jan/20

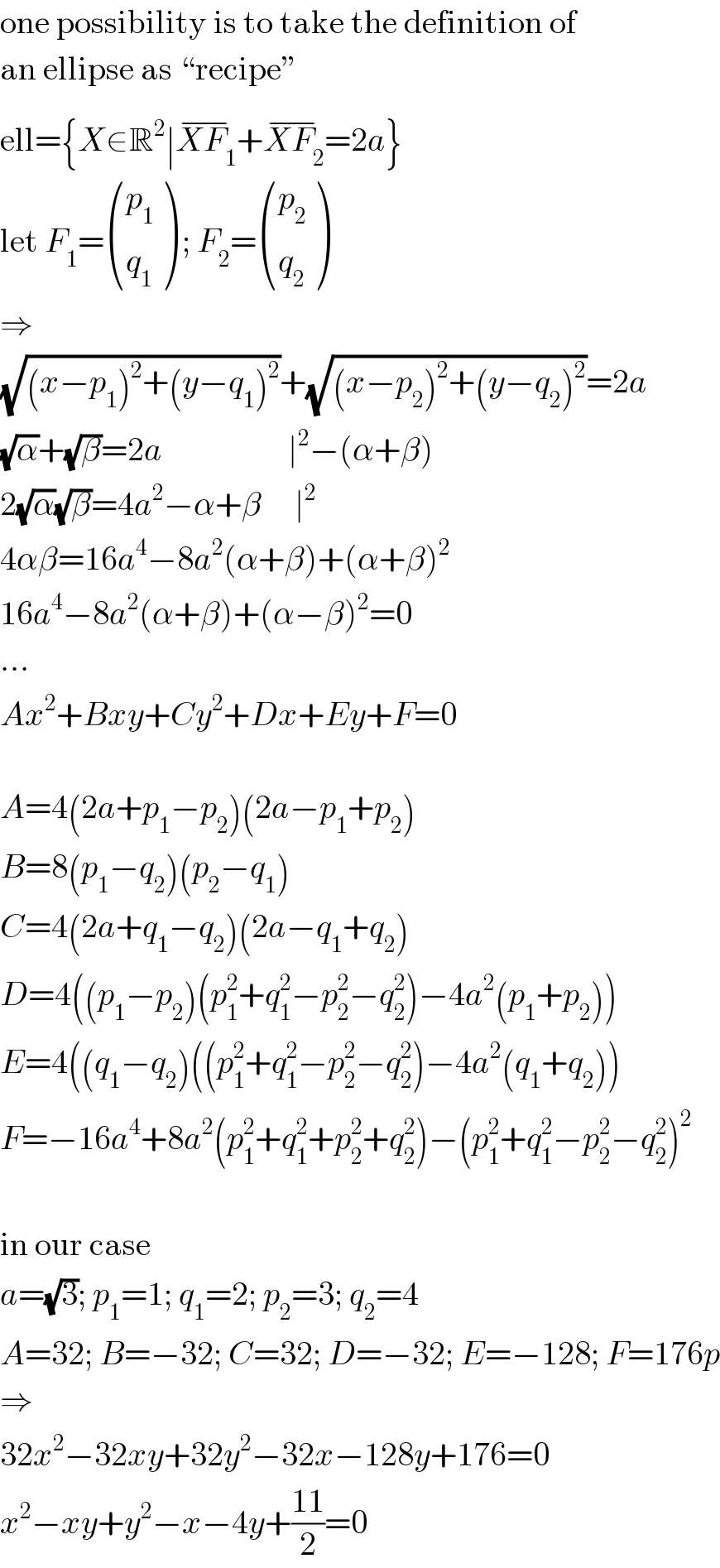
one possibility is to take the definition of an ellipse as “recipe” ell={X∈R^2 ∣XF_1 ^(−) +XF_2 ^(−) =2a} let F_1 = ((p_1 ),(q_1 ) ) ; F_2 = ((p_2 ),(q_2 ) ) ⇒ (√((x−p_1 )^2 +(y−q_1 )^2 ))+(√((x−p_2 )^2 +(y−q_2 )^2 ))=2a (√α)+(√β)=2a ∣^2 −(α+β) 2(√α)(√β)=4a^2 −α+β ∣^2 4αβ=16a^4 −8a^2 (α+β)+(α+β)^2 16a^4 −8a^2 (α+β)+(α−β)^2 =0 ... Ax^2 +Bxy+Cy^2 +Dx+Ey+F=0 A=4(2a+p_1 −p_2 )(2a−p_1 +p_2 ) B=8(p_1 −q_2 )(p_2 −q_1 ) C=4(2a+q_1 −q_2 )(2a−q_1 +q_2 ) D=4((p_1 −p_2 )(p_1 ^2 +q_1 ^2 −p_2 ^2 −q_2 ^2 )−4a^2 (p_1 +p_2 )) E=4((q_1 −q_2 )((p_1 ^2 +q_1 ^2 −p_2 ^2 −q_2 ^2 )−4a^2 (q_1 +q_2 )) F=−16a^4 +8a^2 (p_1 ^2 +q_1 ^2 +p_2 ^2 +q_2 ^2 )−(p_1 ^2 +q_1 ^2 −p_2 ^2 −q_2 ^2 )^2 in our case a=(√3); p_1 =1; q_1 =2; p_2 =3; q_2 =4 A=32; B=−32; C=32; D=−32; E=−128; F=176p ⇒ 32x^2 −32xy+32y^2 −32x−128y+176=0 x^2 −xy+y^2 −x−4y+((11)/2)=0

$$\mathrm{one}\:\mathrm{possibility}\:\mathrm{is}\:\mathrm{to}\:\mathrm{take}\:\mathrm{the}\:\mathrm{definition}\:\mathrm{of} \\ $$$$\mathrm{an}\:\mathrm{ellipse}\:\mathrm{as}\:``\mathrm{recipe}'' \\ $$$$\mathrm{ell}=\left\{{X}\in\mathbb{R}^{\mathrm{2}} \mid\overline {{XF}_{\mathrm{1}} }+\overline {{XF}_{\mathrm{2}} }=\mathrm{2}{a}\right\} \\ $$$$\mathrm{let}\:{F}_{\mathrm{1}} =\begin{pmatrix}{{p}_{\mathrm{1}} }\\{{q}_{\mathrm{1}} }\end{pmatrix}\:;\:{F}_{\mathrm{2}} =\begin{pmatrix}{{p}_{\mathrm{2}} }\\{{q}_{\mathrm{2}} }\end{pmatrix} \\ $$$$\Rightarrow \\ $$$$\sqrt{\left({x}−{p}_{\mathrm{1}} \right)^{\mathrm{2}} +\left({y}−{q}_{\mathrm{1}} \right)^{\mathrm{2}} }+\sqrt{\left({x}−{p}_{\mathrm{2}} \right)^{\mathrm{2}} +\left({y}−{q}_{\mathrm{2}} \right)^{\mathrm{2}} }=\mathrm{2}{a} \\ $$$$\sqrt{\alpha}+\sqrt{\beta}=\mathrm{2}{a}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid^{\mathrm{2}} −\left(\alpha+\beta\right) \\ $$$$\mathrm{2}\sqrt{\alpha}\sqrt{\beta}=\mathrm{4}{a}^{\mathrm{2}} −\alpha+\beta\:\:\:\:\:\mid^{\mathrm{2}} \\ $$$$\mathrm{4}\alpha\beta=\mathrm{16}{a}^{\mathrm{4}} −\mathrm{8}{a}^{\mathrm{2}} \left(\alpha+\beta\right)+\left(\alpha+\beta\right)^{\mathrm{2}} \\ $$$$\mathrm{16}{a}^{\mathrm{4}} −\mathrm{8}{a}^{\mathrm{2}} \left(\alpha+\beta\right)+\left(\alpha−\beta\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$... \\ $$$${Ax}^{\mathrm{2}} +{Bxy}+{Cy}^{\mathrm{2}} +{Dx}+{Ey}+{F}=\mathrm{0} \\ $$$$ \\ $$$${A}=\mathrm{4}\left(\mathrm{2}{a}+{p}_{\mathrm{1}} −{p}_{\mathrm{2}} \right)\left(\mathrm{2}{a}−{p}_{\mathrm{1}} +{p}_{\mathrm{2}} \right) \\ $$$${B}=\mathrm{8}\left({p}_{\mathrm{1}} −{q}_{\mathrm{2}} \right)\left({p}_{\mathrm{2}} −{q}_{\mathrm{1}} \right) \\ $$$${C}=\mathrm{4}\left(\mathrm{2}{a}+{q}_{\mathrm{1}} −{q}_{\mathrm{2}} \right)\left(\mathrm{2}{a}−{q}_{\mathrm{1}} +{q}_{\mathrm{2}} \right) \\ $$$${D}=\mathrm{4}\left(\left({p}_{\mathrm{1}} −{p}_{\mathrm{2}} \right)\left({p}_{\mathrm{1}} ^{\mathrm{2}} +{q}_{\mathrm{1}} ^{\mathrm{2}} −{p}_{\mathrm{2}} ^{\mathrm{2}} −{q}_{\mathrm{2}} ^{\mathrm{2}} \right)−\mathrm{4}{a}^{\mathrm{2}} \left({p}_{\mathrm{1}} +{p}_{\mathrm{2}} \right)\right) \\ $$$${E}=\mathrm{4}\left(\left({q}_{\mathrm{1}} −{q}_{\mathrm{2}} \right)\left(\left({p}_{\mathrm{1}} ^{\mathrm{2}} +{q}_{\mathrm{1}} ^{\mathrm{2}} −{p}_{\mathrm{2}} ^{\mathrm{2}} −{q}_{\mathrm{2}} ^{\mathrm{2}} \right)−\mathrm{4}{a}^{\mathrm{2}} \left({q}_{\mathrm{1}} +{q}_{\mathrm{2}} \right)\right)\right. \\ $$$${F}=−\mathrm{16}{a}^{\mathrm{4}} +\mathrm{8}{a}^{\mathrm{2}} \left({p}_{\mathrm{1}} ^{\mathrm{2}} +{q}_{\mathrm{1}} ^{\mathrm{2}} +{p}_{\mathrm{2}} ^{\mathrm{2}} +{q}_{\mathrm{2}} ^{\mathrm{2}} \right)−\left({p}_{\mathrm{1}} ^{\mathrm{2}} +{q}_{\mathrm{1}} ^{\mathrm{2}} −{p}_{\mathrm{2}} ^{\mathrm{2}} −{q}_{\mathrm{2}} ^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{in}\:\mathrm{our}\:\mathrm{case} \\ $$$${a}=\sqrt{\mathrm{3}};\:{p}_{\mathrm{1}} =\mathrm{1};\:{q}_{\mathrm{1}} =\mathrm{2};\:{p}_{\mathrm{2}} =\mathrm{3};\:{q}_{\mathrm{2}} =\mathrm{4} \\ $$$${A}=\mathrm{32};\:{B}=−\mathrm{32};\:{C}=\mathrm{32};\:{D}=−\mathrm{32};\:{E}=−\mathrm{128};\:{F}=\mathrm{176}{p} \\ $$$$\Rightarrow \\ $$$$\mathrm{32}{x}^{\mathrm{2}} −\mathrm{32}{xy}+\mathrm{32}{y}^{\mathrm{2}} −\mathrm{32}{x}−\mathrm{128}{y}+\mathrm{176}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} −{xy}+{y}^{\mathrm{2}} −{x}−\mathrm{4}{y}+\frac{\mathrm{11}}{\mathrm{2}}=\mathrm{0} \\ $$

Commented by MJS last updated on 15/Jan/20

...you are right with the center point

$$...\mathrm{you}\:\mathrm{are}\:\mathrm{right}\:\mathrm{with}\:\mathrm{the}\:\mathrm{center}\:\mathrm{point} \\ $$

Commented by MJS last updated on 15/Jan/20

the other possibility is to calculate b e=(1/2)F_1 F_2 ^(−) =(√2) b=(√(a^2 −e^2 ))=1 the equation of the ellipse similar to the given one but with center in ((0),(0) ) and axes parallel to x− and y−axes is (x^2 /3)+(y^2 /1)=1 x^2 +3y^2 −3=0 now we have to rotate and shift it θ=∡(F_1 F_2 ^(→) )=45° ⇒ { ((x^∗ =((√2)/2)(x−y))),((y^∗ =((√2)/2)(x+y))) :} ⇔ { ((x=((√2)/2)(x^∗ +y^∗ ))),((y=((√2)/2)(y^∗ −x^∗ ))) :} inserting into our equation 2(x^∗ )^2 −2x^∗ y^∗ +2(y^∗ )^2 −3=0 shifting the center { ((x^∗ =x−2)),((y^∗ =y−3)) :} 2x^2 −2xy+2y^2 −2x−8y+11=0 x^2 −xy+y^2 −x−4y+((11)/2)=0

$$\mathrm{the}\:\mathrm{other}\:\mathrm{possibility}\:\mathrm{is}\:\mathrm{to}\:\mathrm{calculate}\:{b} \\ $$$${e}=\frac{\mathrm{1}}{\mathrm{2}}\overline {{F}_{\mathrm{1}} {F}_{\mathrm{2}} }=\sqrt{\mathrm{2}} \\ $$$${b}=\sqrt{{a}^{\mathrm{2}} −{e}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{the}\:\mathrm{ellipse}\:\mathrm{similar}\:\mathrm{to}\:\mathrm{the} \\ $$$$\mathrm{given}\:\mathrm{one}\:\mathrm{but}\:\mathrm{with}\:\mathrm{center}\:\mathrm{in}\:\begin{pmatrix}{\mathrm{0}}\\{\mathrm{0}}\end{pmatrix}\:\mathrm{and}\:\mathrm{axes} \\ $$$$\mathrm{parallel}\:\mathrm{to}\:{x}−\:\mathrm{and}\:{y}−\mathrm{axes}\:\mathrm{is} \\ $$$$\frac{{x}^{\mathrm{2}} }{\mathrm{3}}+\frac{{y}^{\mathrm{2}} }{\mathrm{1}}=\mathrm{1} \\ $$$${x}^{\mathrm{2}} +\mathrm{3}{y}^{\mathrm{2}} −\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{rotate}\:\mathrm{and}\:\mathrm{shift}\:\mathrm{it} \\ $$$$\theta=\measuredangle\left(\overset{\rightarrow} {{F}_{\mathrm{1}} {F}_{\mathrm{2}} }\right)=\mathrm{45}° \\ $$$$\Rightarrow\:\begin{cases}{{x}^{\ast} =\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left({x}−{y}\right)}\\{{y}^{\ast} =\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left({x}+{y}\right)}\end{cases}\:\Leftrightarrow\:\begin{cases}{{x}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left({x}^{\ast} +{y}^{\ast} \right)}\\{{y}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left({y}^{\ast} −{x}^{\ast} \right)}\end{cases} \\ $$$$\mathrm{inserting}\:\mathrm{into}\:\mathrm{our}\:\mathrm{equation} \\ $$$$\mathrm{2}\left({x}^{\ast} \right)^{\mathrm{2}} −\mathrm{2}{x}^{\ast} {y}^{\ast} +\mathrm{2}\left({y}^{\ast} \right)^{\mathrm{2}} −\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{shifting}\:\mathrm{the}\:\mathrm{center} \\ $$$$\begin{cases}{{x}^{\ast} ={x}−\mathrm{2}}\\{{y}^{\ast} ={y}−\mathrm{3}}\end{cases} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{xy}+\mathrm{2}{y}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{8}{y}+\mathrm{11}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} −{xy}+{y}^{\mathrm{2}} −{x}−\mathrm{4}{y}+\frac{\mathrm{11}}{\mathrm{2}}=\mathrm{0} \\ $$

Commented by jagoll last updated on 15/Jan/20

sir why center point at (0,0) ? and i got the angle α = tan^(−1) (2). where i′m wrong sir?

$${sir}\:{why}\:{center}\:{point}\:{at}\:\left(\mathrm{0},\mathrm{0}\right)\:? \\ $$$${and}\:{i}\:{got}\:{the}\:{angle}\:\alpha\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}\right).\:{where} \\ $$$${i}'{m}\:{wrong}\:{sir}? \\ $$

Commented by MJS last updated on 15/Jan/20

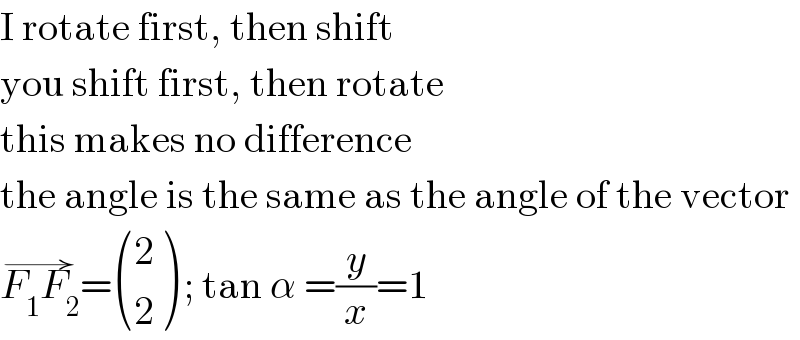
I rotate first, then shift you shift first, then rotate this makes no difference the angle is the same as the angle of the vector F_1 F_2 ^(→) = ((2),(2) ) ; tan α =(y/x)=1

$$\mathrm{I}\:\mathrm{rotate}\:\mathrm{first},\:\mathrm{then}\:\mathrm{shift} \\ $$$$\mathrm{you}\:\mathrm{shift}\:\mathrm{first},\:\mathrm{then}\:\mathrm{rotate} \\ $$$$\mathrm{this}\:\mathrm{makes}\:\mathrm{no}\:\mathrm{difference} \\ $$$$\mathrm{the}\:\mathrm{angle}\:\mathrm{is}\:\mathrm{the}\:\mathrm{same}\:\mathrm{as}\:\mathrm{the}\:\mathrm{angle}\:\mathrm{of}\:\mathrm{the}\:\mathrm{vector} \\ $$$$\overset{\rightarrow} {{F}_{\mathrm{1}} {F}_{\mathrm{2}} }=\begin{pmatrix}{\mathrm{2}}\\{\mathrm{2}}\end{pmatrix}\:;\:\mathrm{tan}\:\alpha\:=\frac{{y}}{{x}}=\mathrm{1} \\ $$

Commented by jagoll last updated on 15/Jan/20

yes sir. thanks

$${yes}\:{sir}.\:{thanks} \\ $$

Answered by jagoll last updated on 15/Jan/20

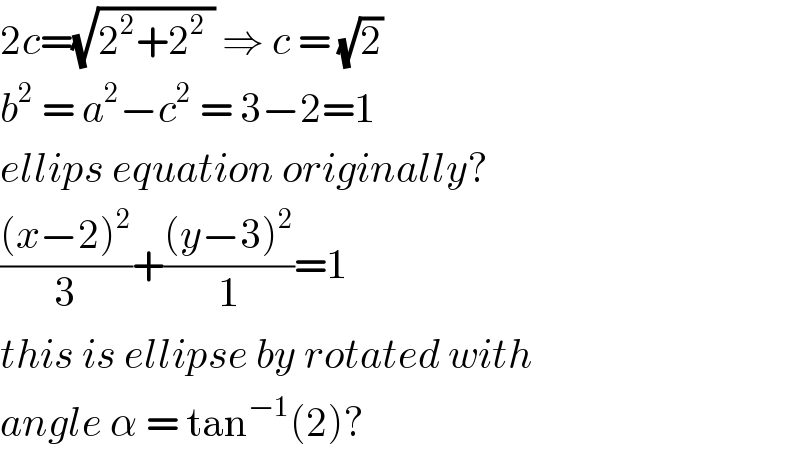
2c=(√(2^2 +2^2 )) ⇒ c = (√2) b^2 = a^2 −c^2 = 3−2=1 ellips equation originally? (((x−2)^2 )/3)+(((y−3)^2 )/1)=1 this is ellipse by rotated with angle α = tan^(−1) (2)?

$$\mathrm{2}{c}=\sqrt{\mathrm{2}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} \:}\:\Rightarrow\:{c}\:=\:\sqrt{\mathrm{2}} \\ $$$${b}^{\mathrm{2}} \:=\:{a}^{\mathrm{2}} −{c}^{\mathrm{2}} \:=\:\mathrm{3}−\mathrm{2}=\mathrm{1} \\ $$$${ellips}\:{equation}\:{originally}? \\ $$$$\frac{\left({x}−\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{3}}+\frac{\left({y}−\mathrm{3}\right)^{\mathrm{2}} }{\mathrm{1}}=\mathrm{1} \\ $$$${this}\:{is}\:{ellipse}\:{by}\:{rotated}\:{with} \\ $$$${angle}\:\alpha\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}\right)? \\ $$

Commented by MJS last updated on 15/Jan/20

angle α=tan^(−1) (1) =45°

$$\mathrm{angle}\:\alpha=\mathrm{tan}^{−\mathrm{1}} \:\left(\mathrm{1}\right)\:=\mathrm{45}° \\ $$

Commented by MJS last updated on 15/Jan/20

...you should get the same result as me. you shift first, then rotate

$$...\mathrm{you}\:\mathrm{should}\:\mathrm{get}\:\mathrm{the}\:\mathrm{same}\:\mathrm{result}\:\mathrm{as}\:\mathrm{me}.\:\mathrm{you} \\ $$$$\mathrm{shift}\:\mathrm{first},\:\mathrm{then}\:\mathrm{rotate} \\ $$

Commented by jagoll last updated on 15/Jan/20

oo tan α =((4−2)/(3−1))=1 . oo i understand sir. thanks you very much

$${oo}\:\mathrm{tan}\:\alpha\:=\frac{\mathrm{4}−\mathrm{2}}{\mathrm{3}−\mathrm{1}}=\mathrm{1}\:.\:{oo}\:{i}\:{understand}\: \\ $$$${sir}.\:{thanks}\:{you}\:{very}\:{much} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com