
Question and Answers Forum
Question Number 78284 by msup trace by abdo last updated on 15/Jan/20
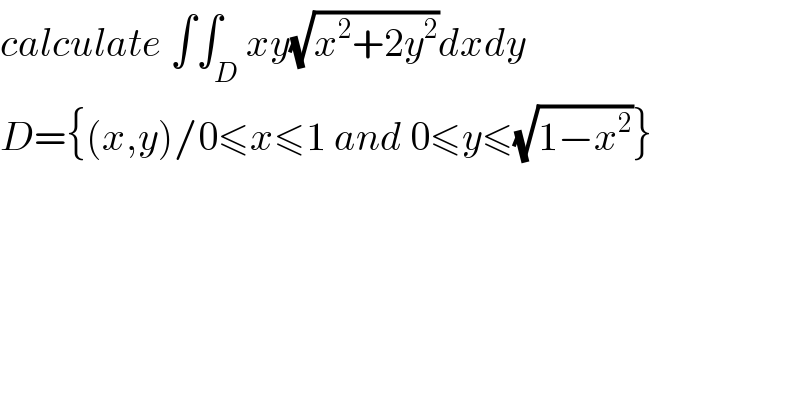
Commented by abdomathmax last updated on 17/Jan/20
![I =∫∫_D xy(√(x^2 +2y^2 ))dxdy ⇒ I =∫_0 ^1 (∫_0 ^(√(1−x^2 )) y(√(x^2 +2y^2 ))dy)xdx but ∫_0 ^(√(1−x^2 )) y(√(x^2 +2y^2 ))dy =[(1/6)(x^2 +2y^2 )^(3/2) ]_0 ^(√(1−x^2 )) =(1/6){ (x^2 +(x^2 +2−2x^2 )^(3/2) −x^3 } =(1/6){ (x^2 −x^3 +(2−x^2 )^(3/2) } ⇒ 6I =∫_0 ^1 x(x^2 −x^3 +(2−x^2 )^(3/2) )dx =∫_0 ^1 (x^3 −x^4 )dx+∫_0 ^1 x(2−x^2 )^(3/2) dx =[(x^4 /4)−(x^5 /5)]_0 ^1 +∫_0 ^1 x(2−x^2 )^(3/2) dx =(1/(20)) +∫_0 ^1 x(2−x^2 )^(3/2) dx we have ∫_0 ^1 x(2−x^2 )^(3/2) dx =_(x=(√2)sint) ∫_0 ^(π/4) (√2)sint(2−2sin^2 t)^(3/2) (√2)costdt =2×2^(3/2) ∫_0 ^(π/4) sint cos^4 t dt =2^(5/2) [−(1/5)cos^5 t]_0 ^(π/4) =−((4(√2))/5)( ((1/(√2)))^5 −1) =−((4(√2))/5)( (1/(4(√2)))−1) =−(1/5)+((4(√2))/5) ⇒ 6I =(1/(20))−(1/5) +((4(√2))/5) =((−3)/(20)) +((4(√2))/5) ⇒ I =−(1/(40)) +((2(√2))/(15))](Q78430.png)
| ||
Question and Answers Forum | ||
Question Number 78284 by msup trace by abdo last updated on 15/Jan/20 | ||
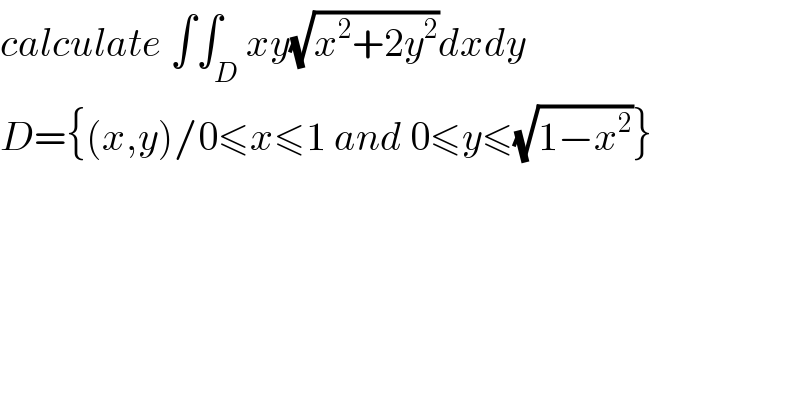 | ||
Commented by abdomathmax last updated on 17/Jan/20 | ||
![I =∫∫_D xy(√(x^2 +2y^2 ))dxdy ⇒ I =∫_0 ^1 (∫_0 ^(√(1−x^2 )) y(√(x^2 +2y^2 ))dy)xdx but ∫_0 ^(√(1−x^2 )) y(√(x^2 +2y^2 ))dy =[(1/6)(x^2 +2y^2 )^(3/2) ]_0 ^(√(1−x^2 )) =(1/6){ (x^2 +(x^2 +2−2x^2 )^(3/2) −x^3 } =(1/6){ (x^2 −x^3 +(2−x^2 )^(3/2) } ⇒ 6I =∫_0 ^1 x(x^2 −x^3 +(2−x^2 )^(3/2) )dx =∫_0 ^1 (x^3 −x^4 )dx+∫_0 ^1 x(2−x^2 )^(3/2) dx =[(x^4 /4)−(x^5 /5)]_0 ^1 +∫_0 ^1 x(2−x^2 )^(3/2) dx =(1/(20)) +∫_0 ^1 x(2−x^2 )^(3/2) dx we have ∫_0 ^1 x(2−x^2 )^(3/2) dx =_(x=(√2)sint) ∫_0 ^(π/4) (√2)sint(2−2sin^2 t)^(3/2) (√2)costdt =2×2^(3/2) ∫_0 ^(π/4) sint cos^4 t dt =2^(5/2) [−(1/5)cos^5 t]_0 ^(π/4) =−((4(√2))/5)( ((1/(√2)))^5 −1) =−((4(√2))/5)( (1/(4(√2)))−1) =−(1/5)+((4(√2))/5) ⇒ 6I =(1/(20))−(1/5) +((4(√2))/5) =((−3)/(20)) +((4(√2))/5) ⇒ I =−(1/(40)) +((2(√2))/(15))](Q78430.png) | ||