
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 78286 by msup trace by abdo last updated on 15/Jan/20
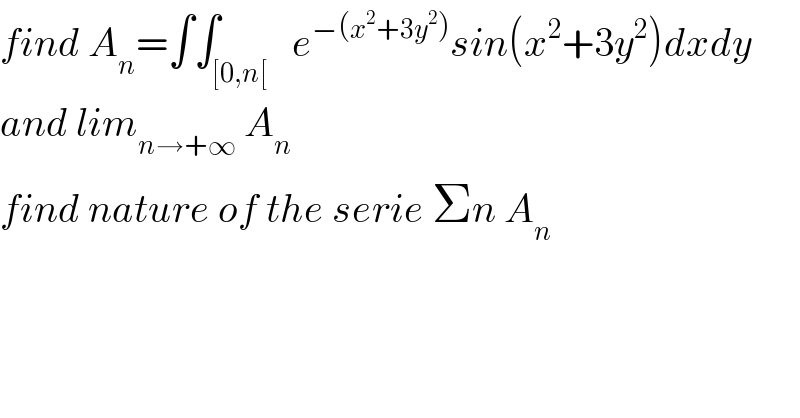
Commented by mathmax by abdo last updated on 16/Jan/20
![changement x=rcosθ and y =(r/(√3))sinθ give x^2 +3y^2 =r^2 0≤x≤n and 0≤y≤n ⇒0≤x^2 +y^2 ≤2n^2 ⇒0≤r≤n(√2) θ ∈[0,(π/2)] diffemorphisme is (r,θ)→(x,y)=(ϕ_1 ,ϕ_2 )(rcosθ,(r/(√3))sinθ) M_j (ϕ) = ((((∂ϕ_1 /∂r) (∂ϕ_1 /∂θ))),(((∂ϕ_2 /∂r) (∂ϕ_2 /∂θ))) ) = (((cosθ −rsinθ )),((((sinθ)/(√3)) (r/(√3))cosθ)) ) ⇒det(M_j ) =(r/(√3)) ⇒ A_n =∫_0 ^(π/2) ∫_0 ^(n(√2)) e^(−r^2 ) sin(r^2 )(r/(√3))dr dθ =(π/(2(√3))) ∫_0 ^(n(√2)) r e^(−r^2 ) sin(r^2 )dr by parts u^′ =re^(−r^2 ) and v=sin(r^2 ) A_n =(π/(2(√3))){ [−(1/2)e^(−r^2 ) sin(r^2 )]_0 ^(n(√2)) −∫_0 ^(n(√2)) (−(1/2)e^(−r^2 ) ×2rcos(r^2 ))dr} =(π/(2(√3))){−(1/2)e^(−2n^2 ) sin(2n^2 )+∫_0 ^(n(√2)) r e^(−r^2 ) cos(r^2 )dr} =(π/(2(√3))){ −(1/2)e^(−2n^2 ) sin(2n^2 )+[−(1/2)e^(−r^2 ) cos(r^2 )]_0 ^(n(√2)) −∫_0 ^(n(√2)) (−(1/2)e^(−r^2 ) (−2r sin(r^2 ))dr =(π/(2(√3))){−(1/2)e^(−2n^2 ) sin(2n^2 )+(1/2)−(1/2)e^(−2n^2 ) cos(2n^2 )−∫_0 ^(n(√2)) r e^(−r^2 ) sin(r^2 )dr} ⇒2A_n =(π/(4(√3))){1−e^(−2n^2 ) sin(2n^2 )−e^(−2n^2 ) cos(2n^2 )} ⇒ A_n =(π/(8(√3))){ 1−e^(−2n^2 ) sin(2n^2 )−e^(−2n^2 ) cos(2n^2 )} we have lim_(n→+∞) e^(−2n^2 ) sin(2n^2 )=lim_(n→+∞) e^(−2n^2 ) cos(2n^2 )=0 ⇒ lim_(n→+∞) A_n =(π/(8(√3)))](Q78388.png)
| ||
Question and Answers Forum | ||
Previous in Relation and Functions Next in Relation and Functions | ||
Question Number 78286 by msup trace by abdo last updated on 15/Jan/20 | ||
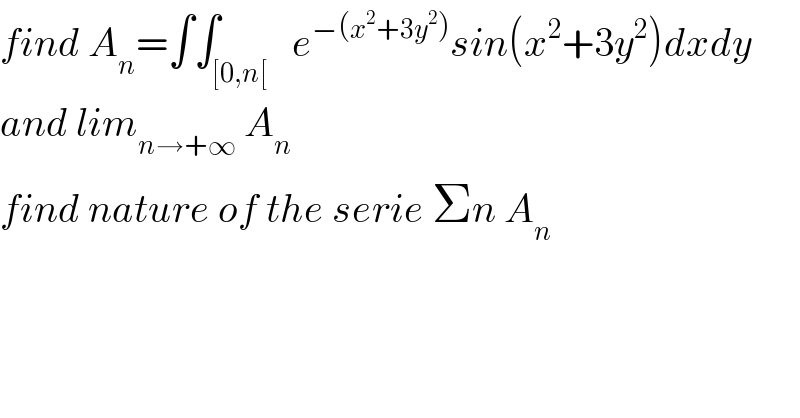 | ||
Commented by mathmax by abdo last updated on 16/Jan/20 | ||
![changement x=rcosθ and y =(r/(√3))sinθ give x^2 +3y^2 =r^2 0≤x≤n and 0≤y≤n ⇒0≤x^2 +y^2 ≤2n^2 ⇒0≤r≤n(√2) θ ∈[0,(π/2)] diffemorphisme is (r,θ)→(x,y)=(ϕ_1 ,ϕ_2 )(rcosθ,(r/(√3))sinθ) M_j (ϕ) = ((((∂ϕ_1 /∂r) (∂ϕ_1 /∂θ))),(((∂ϕ_2 /∂r) (∂ϕ_2 /∂θ))) ) = (((cosθ −rsinθ )),((((sinθ)/(√3)) (r/(√3))cosθ)) ) ⇒det(M_j ) =(r/(√3)) ⇒ A_n =∫_0 ^(π/2) ∫_0 ^(n(√2)) e^(−r^2 ) sin(r^2 )(r/(√3))dr dθ =(π/(2(√3))) ∫_0 ^(n(√2)) r e^(−r^2 ) sin(r^2 )dr by parts u^′ =re^(−r^2 ) and v=sin(r^2 ) A_n =(π/(2(√3))){ [−(1/2)e^(−r^2 ) sin(r^2 )]_0 ^(n(√2)) −∫_0 ^(n(√2)) (−(1/2)e^(−r^2 ) ×2rcos(r^2 ))dr} =(π/(2(√3))){−(1/2)e^(−2n^2 ) sin(2n^2 )+∫_0 ^(n(√2)) r e^(−r^2 ) cos(r^2 )dr} =(π/(2(√3))){ −(1/2)e^(−2n^2 ) sin(2n^2 )+[−(1/2)e^(−r^2 ) cos(r^2 )]_0 ^(n(√2)) −∫_0 ^(n(√2)) (−(1/2)e^(−r^2 ) (−2r sin(r^2 ))dr =(π/(2(√3))){−(1/2)e^(−2n^2 ) sin(2n^2 )+(1/2)−(1/2)e^(−2n^2 ) cos(2n^2 )−∫_0 ^(n(√2)) r e^(−r^2 ) sin(r^2 )dr} ⇒2A_n =(π/(4(√3))){1−e^(−2n^2 ) sin(2n^2 )−e^(−2n^2 ) cos(2n^2 )} ⇒ A_n =(π/(8(√3))){ 1−e^(−2n^2 ) sin(2n^2 )−e^(−2n^2 ) cos(2n^2 )} we have lim_(n→+∞) e^(−2n^2 ) sin(2n^2 )=lim_(n→+∞) e^(−2n^2 ) cos(2n^2 )=0 ⇒ lim_(n→+∞) A_n =(π/(8(√3)))](Q78388.png) | ||