Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 78357 by TawaTawa last updated on 16/Jan/20

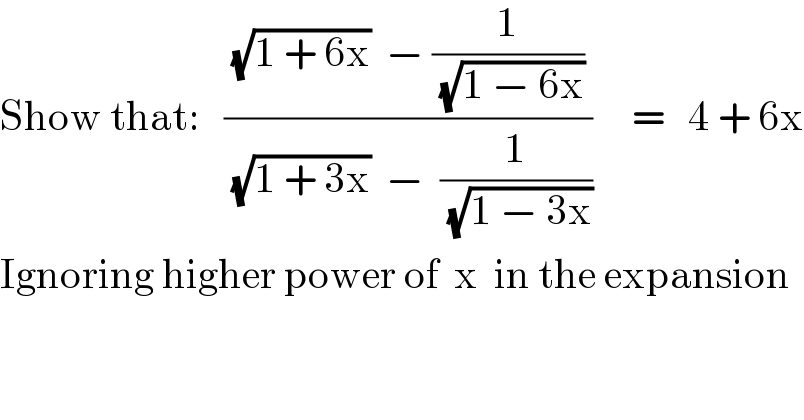
Show that: (((√(1 + 6x)) − (1/(√(1 − 6x))))/((√(1 + 3x)) − (1/(√(1 − 3x))))) = 4 + 6x Ignoring higher power of x in the expansion

$$\mathrm{Show}\:\mathrm{that}:\:\:\:\frac{\sqrt{\mathrm{1}\:+\:\mathrm{6x}}\:\:−\:\frac{\mathrm{1}}{\sqrt{\mathrm{1}\:−\:\mathrm{6x}}}}{\sqrt{\mathrm{1}\:+\:\mathrm{3x}}\:\:−\:\:\frac{\mathrm{1}}{\sqrt{\mathrm{1}\:−\:\mathrm{3x}}}}\:\:\:\:\:=\:\:\:\mathrm{4}\:+\:\mathrm{6x} \\ $$$$\mathrm{Ignoring}\:\mathrm{higher}\:\mathrm{power}\:\mathrm{of}\:\:\mathrm{x}\:\:\mathrm{in}\:\mathrm{the}\:\mathrm{expansion} \\ $$

Commented by MJS last updated on 16/Jan/20

I don′t understand this question the left handed side is defined for −(1/6)≤x<(1/6)∧x≠0 it has an absolute minimum at x≈−.060524; y≈3.82364 its range is 3.82364<y<+∞ how can this be equal to a straight line?

$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{understand}\:\mathrm{this}\:\mathrm{question} \\ $$$$\mathrm{the}\:\mathrm{left}\:\mathrm{handed}\:\mathrm{side}\:\mathrm{is}\:\mathrm{defined}\:\mathrm{for} \\ $$$$−\frac{\mathrm{1}}{\mathrm{6}}\leqslant{x}<\frac{\mathrm{1}}{\mathrm{6}}\wedge{x}\neq\mathrm{0} \\ $$$$\mathrm{it}\:\mathrm{has}\:\mathrm{an}\:\mathrm{absolute}\:\mathrm{minimum}\:\mathrm{at} \\ $$$${x}\approx−.\mathrm{060524};\:{y}\approx\mathrm{3}.\mathrm{82364} \\ $$$$\mathrm{its}\:\mathrm{range}\:\mathrm{is}\:\mathrm{3}.\mathrm{82364}<{y}<+\infty \\ $$$$\mathrm{how}\:\mathrm{can}\:\mathrm{this}\:\mathrm{be}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{a}\:\mathrm{straight}\:\mathrm{line}? \\ $$

Commented by TawaTawa last updated on 16/Jan/20

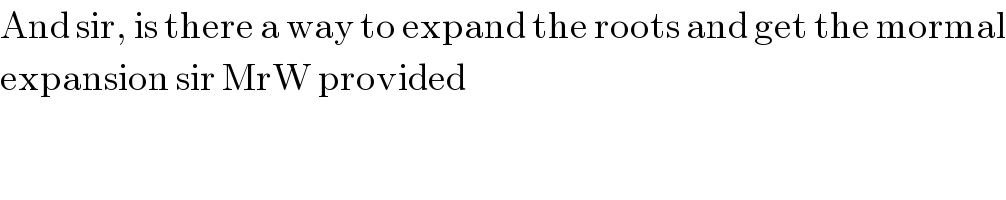
And sir, is there a way to expand the roots and get the mormal expansion sir MrW provided

$$\mathrm{And}\:\mathrm{sir},\:\mathrm{is}\:\mathrm{there}\:\mathrm{a}\:\mathrm{way}\:\mathrm{to}\:\mathrm{expand}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{and}\:\mathrm{get}\:\mathrm{the}\:\mathrm{mormal} \\ $$$$\mathrm{expansion}\:\mathrm{sir}\:\mathrm{MrW}\:\mathrm{provided} \\ $$

Commented by TawaTawa last updated on 16/Jan/20

Sir it is if x is so small. prove the above.

$$\mathrm{Sir}\:\mathrm{it}\:\mathrm{is}\:\mathrm{if}\:\:\mathrm{x}\:\mathrm{is}\:\mathrm{so}\:\mathrm{small}.\:\mathrm{prove}\:\mathrm{the}\:\mathrm{above}. \\ $$

Commented by MJS last updated on 16/Jan/20

lim_(x→0) (lhs) =4 and lim_(x→0) ((d/dx)[lhs]) =6 ⇒ the tangent in x=0 is indeed 6x+4 but it′s not easy to expand the lhs

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{lhs}\right)\:=\mathrm{4}\:\mathrm{and}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{{d}}{{dx}}\left[\mathrm{lhs}\right]\right)\:=\mathrm{6}\:\Rightarrow \\ $$$$\mathrm{the}\:\mathrm{tangent}\:\mathrm{in}\:{x}=\mathrm{0}\:\mathrm{is}\:\mathrm{indeed}\:\mathrm{6}{x}+\mathrm{4} \\ $$$$\mathrm{but}\:\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{expand}\:\mathrm{the}\:\mathrm{lhs} \\ $$

Commented by mathmax by abdo last updated on 16/Jan/20

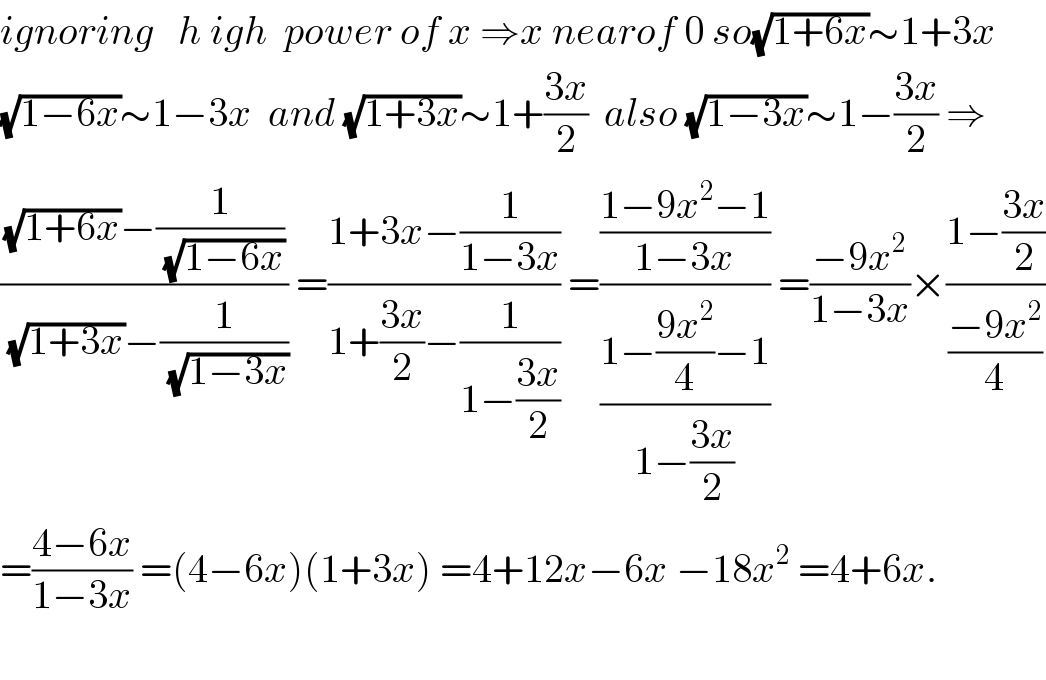
ignoring h igh power of x ⇒x nearof 0 so(√(1+6x))∼1+3x (√(1−6x))∼1−3x and (√(1+3x))∼1+((3x)/2) also (√(1−3x))∼1−((3x)/2) ⇒ (((√(1+6x))−(1/(√(1−6x))))/((√(1+3x))−(1/(√(1−3x))))) =((1+3x−(1/(1−3x)))/(1+((3x)/2)−(1/(1−((3x)/2))))) =(((1−9x^2 −1)/(1−3x))/((1−((9x^2 )/4)−1)/(1−((3x)/2)))) =((−9x^2 )/(1−3x))×((1−((3x)/2))/((−9x^2 )/4)) =((4−6x)/(1−3x)) =(4−6x)(1+3x) =4+12x−6x −18x^2 =4+6x.

$${ignoring}\:\:\:{h}\:{igh}\:\:{power}\:{of}\:{x}\:\Rightarrow{x}\:{nearof}\:\mathrm{0}\:{so}\sqrt{\mathrm{1}+\mathrm{6}{x}}\sim\mathrm{1}+\mathrm{3}{x} \\ $$$$\sqrt{\mathrm{1}−\mathrm{6}{x}}\sim\mathrm{1}−\mathrm{3}{x}\:\:{and}\:\sqrt{\mathrm{1}+\mathrm{3}{x}}\sim\mathrm{1}+\frac{\mathrm{3}{x}}{\mathrm{2}}\:\:{also}\:\sqrt{\mathrm{1}−\mathrm{3}{x}}\sim\mathrm{1}−\frac{\mathrm{3}{x}}{\mathrm{2}}\:\Rightarrow \\ $$$$\frac{\sqrt{\mathrm{1}+\mathrm{6}{x}}−\frac{\mathrm{1}}{\sqrt{\mathrm{1}−\mathrm{6}{x}}}}{\sqrt{\mathrm{1}+\mathrm{3}{x}}−\frac{\mathrm{1}}{\sqrt{\mathrm{1}−\mathrm{3}{x}}}}\:=\frac{\mathrm{1}+\mathrm{3}{x}−\frac{\mathrm{1}}{\mathrm{1}−\mathrm{3}{x}}}{\mathrm{1}+\frac{\mathrm{3}{x}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{3}{x}}{\mathrm{2}}}}\:=\frac{\frac{\mathrm{1}−\mathrm{9}{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}−\mathrm{3}{x}}}{\frac{\mathrm{1}−\frac{\mathrm{9}{x}^{\mathrm{2}} }{\mathrm{4}}−\mathrm{1}}{\mathrm{1}−\frac{\mathrm{3}{x}}{\mathrm{2}}}}\:=\frac{−\mathrm{9}{x}^{\mathrm{2}} }{\mathrm{1}−\mathrm{3}{x}}×\frac{\mathrm{1}−\frac{\mathrm{3}{x}}{\mathrm{2}}}{\frac{−\mathrm{9}{x}^{\mathrm{2}} }{\mathrm{4}}} \\ $$$$=\frac{\mathrm{4}−\mathrm{6}{x}}{\mathrm{1}−\mathrm{3}{x}}\:=\left(\mathrm{4}−\mathrm{6}{x}\right)\left(\mathrm{1}+\mathrm{3}{x}\right)\:=\mathrm{4}+\mathrm{12}{x}−\mathrm{6}{x}\:−\mathrm{18}{x}^{\mathrm{2}} \:=\mathrm{4}+\mathrm{6}{x}. \\ $$$$ \\ $$

Commented by TawaTawa last updated on 16/Jan/20

Wow, God bless you sir.

$$\mathrm{Wow},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Commented by mathmax by abdo last updated on 17/Jan/20

you are welcome

$${you}\:{are}\:{welcome} \\ $$

Answered by Kunal12588 last updated on 16/Jan/20

(((√(1 + 6x)) − (1/(√(1 − 6x))))/((√(1 + 3x)) − (1/(√(1 − 3x))))) =((1 + 6x −1)/(1 + 3x − 1))×((√(1−3x))/(√(1−6x))) =2(√((1−3x)/(1−6x))) now we have to proove (2+3x)^2 =((1−3x)/(1−6x)) ⇒(4+12x+9x^2 )(1−6x)=1−3x ⇒4+12x+9x^2 −24x−72x^2 −54x^3 =1−3x ⇒3−9x−63x^2 −54x^3 =0 ⇒18x^3 +21x^2 +3x−1=0 so the values satisfying this equation can be the solution of the equation. this is not true everywhere. ∴ we can not prove your equation

$$\frac{\sqrt{\mathrm{1}\:+\:\mathrm{6x}}\:\:−\:\frac{\mathrm{1}}{\sqrt{\mathrm{1}\:−\:\mathrm{6x}}}}{\sqrt{\mathrm{1}\:+\:\mathrm{3x}}\:\:−\:\:\frac{\mathrm{1}}{\sqrt{\mathrm{1}\:−\:\mathrm{3x}}}} \\ $$$$=\frac{\mathrm{1}\:+\:\mathrm{6x}\:−\mathrm{1}}{\mathrm{1}\:+\:\mathrm{3x}\:\:−\:\:\mathrm{1}}×\frac{\sqrt{\mathrm{1}−\mathrm{3}{x}}}{\sqrt{\mathrm{1}−\mathrm{6}{x}}} \\ $$$$=\mathrm{2}\sqrt{\frac{\mathrm{1}−\mathrm{3}{x}}{\mathrm{1}−\mathrm{6}{x}}} \\ $$$${now}\:{we}\:{have}\:{to}\:{proove} \\ $$$$\left(\mathrm{2}+\mathrm{3}{x}\right)^{\mathrm{2}} =\frac{\mathrm{1}−\mathrm{3}{x}}{\mathrm{1}−\mathrm{6}{x}} \\ $$$$\Rightarrow\left(\mathrm{4}+\mathrm{12}{x}+\mathrm{9}{x}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{6}{x}\right)=\mathrm{1}−\mathrm{3}{x} \\ $$$$\Rightarrow\mathrm{4}+\mathrm{12}{x}+\mathrm{9}{x}^{\mathrm{2}} −\mathrm{24}{x}−\mathrm{72}{x}^{\mathrm{2}} −\mathrm{54}{x}^{\mathrm{3}} =\mathrm{1}−\mathrm{3}{x} \\ $$$$\Rightarrow\mathrm{3}−\mathrm{9}{x}−\mathrm{63}{x}^{\mathrm{2}} −\mathrm{54}{x}^{\mathrm{3}} =\mathrm{0} \\ $$$$\Rightarrow\mathrm{18}{x}^{\mathrm{3}} +\mathrm{21}{x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{1}=\mathrm{0} \\ $$$${so}\:{the}\:{values}\:{satisfying}\:{this}\:{equation}\:{can} \\ $$$${be}\:{the}\:{solution}\:{of}\:{the}\:{equation}.\:{this}\:{is}\:{not}\: \\ $$$${true}\:{everywhere}. \\ $$$$\therefore\:{we}\:{can}\:{not}\:{prove}\:{your}\:{equation} \\ $$

Commented by TawaTawa last updated on 16/Jan/20

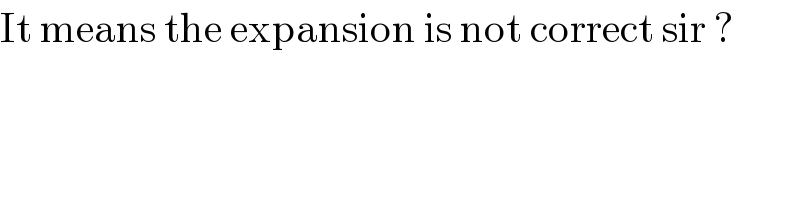
It means the expansion is not correct sir ?

$$\mathrm{It}\:\mathrm{means}\:\mathrm{the}\:\mathrm{expansion}\:\mathrm{is}\:\mathrm{not}\:\mathrm{correct}\:\mathrm{sir}\:? \\ $$

Commented by mr W last updated on 16/Jan/20

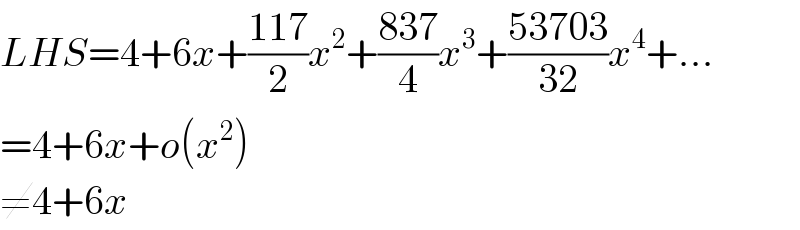
LHS=4+6x+((117)/2)x^2 +((837)/4)x^3 +((53703)/(32))x^4 +... =4+6x+o(x^2 ) ≠4+6x

$${LHS}=\mathrm{4}+\mathrm{6}{x}+\frac{\mathrm{117}}{\mathrm{2}}{x}^{\mathrm{2}} +\frac{\mathrm{837}}{\mathrm{4}}{x}^{\mathrm{3}} +\frac{\mathrm{53703}}{\mathrm{32}}{x}^{\mathrm{4}} +... \\ $$$$=\mathrm{4}+\mathrm{6}{x}+{o}\left({x}^{\mathrm{2}} \right) \\ $$$$\neq\mathrm{4}+\mathrm{6}{x} \\ $$

Commented by TawaTawa last updated on 16/Jan/20

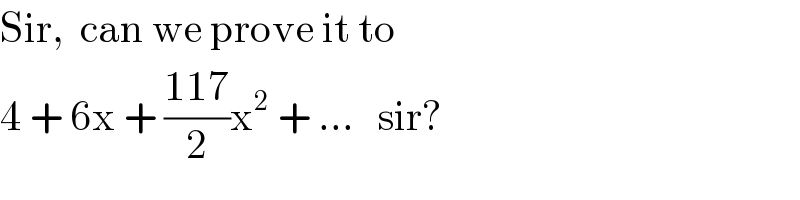
Sir, can we prove it to 4 + 6x + ((117)/2)x^2 + ... sir?

$$\mathrm{Sir},\:\:\mathrm{can}\:\mathrm{we}\:\mathrm{prove}\:\mathrm{it}\:\mathrm{to} \\ $$$$\mathrm{4}\:+\:\mathrm{6x}\:+\:\frac{\mathrm{117}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \:+\:...\:\:\:\mathrm{sir}? \\ $$

Commented by mr W last updated on 16/Jan/20

we can prove LHS=4+o(x) LHS=4+6x+o(x^2 ) LHS=4+6x+((117)/2)x^2 +o(x^3 ) LHS=4+6x+((117)/2)x^2 +((837)/4)x^3 +o(x^4 ) LHS=4+6x+((117)/2)x^2 +((837)/4)x^3 +((53703)/(32))x^4 +o(x^5 ) etc. but we can not prove LHS=4+6x

$${we}\:{can}\:{prove} \\ $$$${LHS}=\mathrm{4}+{o}\left({x}\right) \\ $$$${LHS}=\mathrm{4}+\mathrm{6}{x}+{o}\left({x}^{\mathrm{2}} \right) \\ $$$${LHS}=\mathrm{4}+\mathrm{6}{x}+\frac{\mathrm{117}}{\mathrm{2}}{x}^{\mathrm{2}} +{o}\left({x}^{\mathrm{3}} \right) \\ $$$${LHS}=\mathrm{4}+\mathrm{6}{x}+\frac{\mathrm{117}}{\mathrm{2}}{x}^{\mathrm{2}} +\frac{\mathrm{837}}{\mathrm{4}}{x}^{\mathrm{3}} +{o}\left({x}^{\mathrm{4}} \right) \\ $$$${LHS}=\mathrm{4}+\mathrm{6}{x}+\frac{\mathrm{117}}{\mathrm{2}}{x}^{\mathrm{2}} +\frac{\mathrm{837}}{\mathrm{4}}{x}^{\mathrm{3}} +\frac{\mathrm{53703}}{\mathrm{32}}{x}^{\mathrm{4}} +{o}\left({x}^{\mathrm{5}} \right) \\ $$$${etc}. \\ $$$${but}\:{we}\:{can}\:{not}\:{prove} \\ $$$${LHS}=\mathrm{4}+\mathrm{6}{x} \\ $$

Commented by TawaTawa last updated on 16/Jan/20

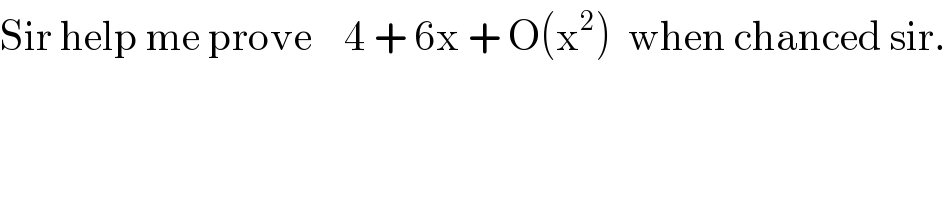
Sir help me prove 4 + 6x + O(x^2 ) when chanced sir.

$$\mathrm{Sir}\:\mathrm{help}\:\mathrm{me}\:\mathrm{prove}\:\:\:\:\mathrm{4}\:+\:\mathrm{6x}\:+\:\mathrm{O}\left(\mathrm{x}^{\mathrm{2}} \right)\:\:\mathrm{when}\:\mathrm{chanced}\:\mathrm{sir}. \\ $$

Commented by TawaTawa last updated on 16/Jan/20

Thanks for your time.

$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}. \\ $$

Commented by mr W last updated on 16/Jan/20

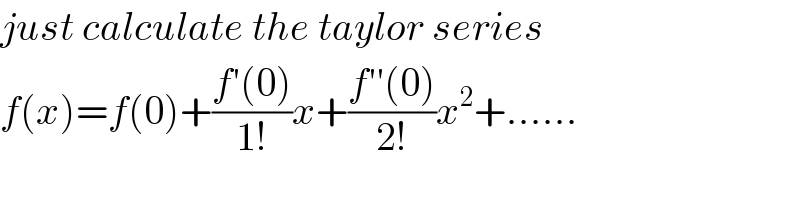
just calculate the taylor series f(x)=f(0)+((f′(0))/(1!))x+((f′′(0))/(2!))x^2 +......

$${just}\:{calculate}\:{the}\:{taylor}\:{series}\: \\ $$$${f}\left({x}\right)={f}\left(\mathrm{0}\right)+\frac{{f}'\left(\mathrm{0}\right)}{\mathrm{1}!}{x}+\frac{{f}''\left(\mathrm{0}\right)}{\mathrm{2}!}{x}^{\mathrm{2}} +...... \\ $$

Commented by MJS last updated on 16/Jan/20

Sir mrW, what about my idea using the limits?

$$\mathrm{Sir}\:\mathrm{mrW},\:\mathrm{what}\:\mathrm{about}\:\mathrm{my}\:\mathrm{idea}\:\mathrm{using}\:\mathrm{the}\:\mathrm{limits}? \\ $$

Commented by mr W last updated on 16/Jan/20

good idea sir! we even have to use limits here, since lhs is not defined at x=0.

$${good}\:{idea}\:{sir}!\:{we}\:{even}\:{have}\:{to}\:{use} \\ $$$${limits}\:{here},\:{since}\:{lhs}\:{is}\:{not}\:{defined} \\ $$$${at}\:{x}=\mathrm{0}. \\ $$

Commented by TawaTawa last updated on 16/Jan/20

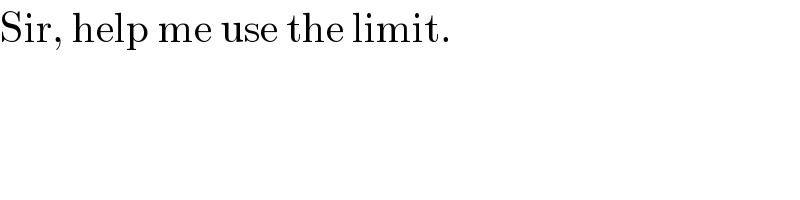
Sir, help me use the limit.

$$\mathrm{Sir},\:\mathrm{help}\:\mathrm{me}\:\mathrm{use}\:\mathrm{the}\:\mathrm{limit}. \\ $$

Commented by mr W last updated on 16/Jan/20

a piece of pure routine work! try DIY!

$${a}\:{piece}\:{of}\:{pure}\:{routine}\:{work}!\:{try}\:{DIY}! \\ $$

Answered by mr W last updated on 16/Jan/20

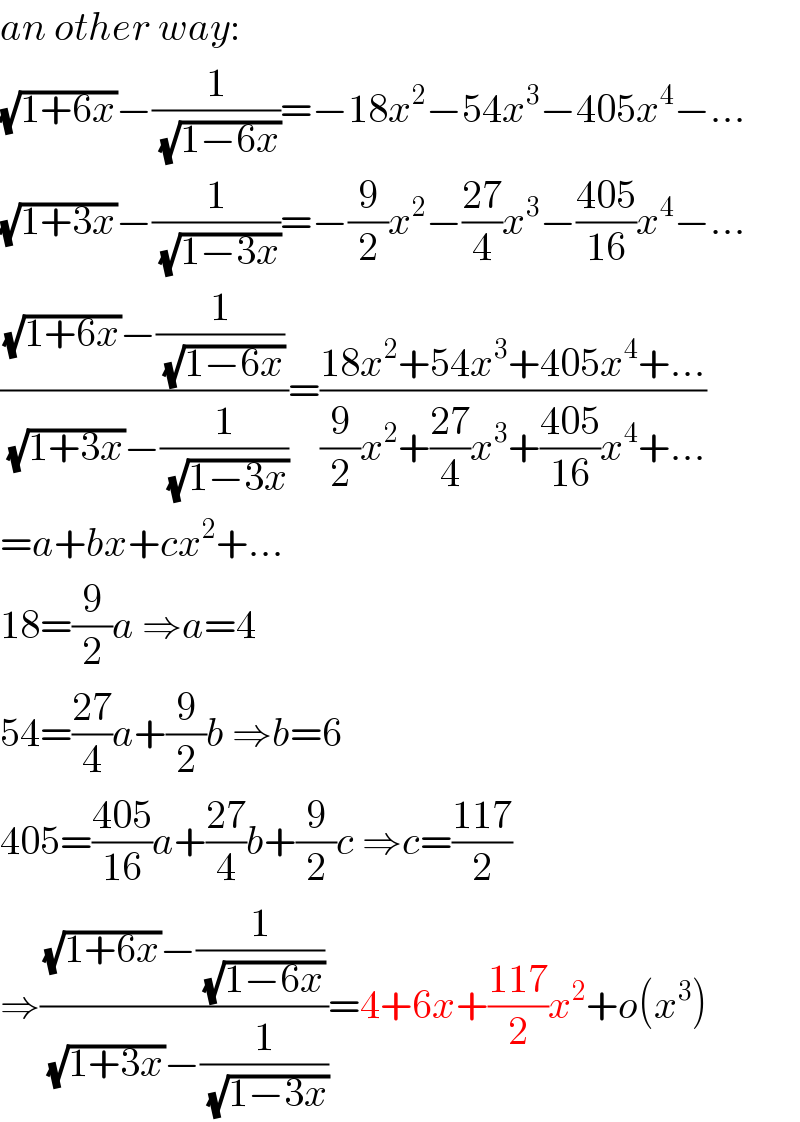
an other way: (√(1+6x))−(1/(√(1−6x)))=−18x^2 −54x^3 −405x^4 −... (√(1+3x))−(1/(√(1−3x)))=−(9/2)x^2 −((27)/4)x^3 −((405)/(16))x^4 −... (((√(1+6x))−(1/(√(1−6x))))/((√(1+3x))−(1/(√(1−3x)))))=((18x^2 +54x^3 +405x^4 +...)/((9/2)x^2 +((27)/4)x^3 +((405)/(16))x^4 +...)) =a+bx+cx^2 +... 18=(9/2)a ⇒a=4 54=((27)/4)a+(9/2)b ⇒b=6 405=((405)/(16))a+((27)/4)b+(9/2)c ⇒c=((117)/2) ⇒(((√(1+6x))−(1/(√(1−6x))))/((√(1+3x))−(1/(√(1−3x)))))=4+6x+((117)/2)x^2 +o(x^3 )

$${an}\:{other}\:{way}: \\ $$$$\sqrt{\mathrm{1}+\mathrm{6}{x}}−\frac{\mathrm{1}}{\sqrt{\mathrm{1}−\mathrm{6}{x}}}=−\mathrm{18}{x}^{\mathrm{2}} −\mathrm{54}{x}^{\mathrm{3}} −\mathrm{405}{x}^{\mathrm{4}} −... \\ $$$$\sqrt{\mathrm{1}+\mathrm{3}{x}}−\frac{\mathrm{1}}{\sqrt{\mathrm{1}−\mathrm{3}{x}}}=−\frac{\mathrm{9}}{\mathrm{2}}{x}^{\mathrm{2}} −\frac{\mathrm{27}}{\mathrm{4}}{x}^{\mathrm{3}} −\frac{\mathrm{405}}{\mathrm{16}}{x}^{\mathrm{4}} −... \\ $$$$\frac{\sqrt{\mathrm{1}+\mathrm{6}{x}}−\frac{\mathrm{1}}{\sqrt{\mathrm{1}−\mathrm{6}{x}}}}{\sqrt{\mathrm{1}+\mathrm{3}{x}}−\frac{\mathrm{1}}{\sqrt{\mathrm{1}−\mathrm{3}{x}}}}=\frac{\mathrm{18}{x}^{\mathrm{2}} +\mathrm{54}{x}^{\mathrm{3}} +\mathrm{405}{x}^{\mathrm{4}} +...}{\frac{\mathrm{9}}{\mathrm{2}}{x}^{\mathrm{2}} +\frac{\mathrm{27}}{\mathrm{4}}{x}^{\mathrm{3}} +\frac{\mathrm{405}}{\mathrm{16}}{x}^{\mathrm{4}} +...} \\ $$$$={a}+{bx}+{cx}^{\mathrm{2}} +... \\ $$$$\mathrm{18}=\frac{\mathrm{9}}{\mathrm{2}}{a}\:\Rightarrow{a}=\mathrm{4} \\ $$$$\mathrm{54}=\frac{\mathrm{27}}{\mathrm{4}}{a}+\frac{\mathrm{9}}{\mathrm{2}}{b}\:\Rightarrow{b}=\mathrm{6} \\ $$$$\mathrm{405}=\frac{\mathrm{405}}{\mathrm{16}}{a}+\frac{\mathrm{27}}{\mathrm{4}}{b}+\frac{\mathrm{9}}{\mathrm{2}}{c}\:\Rightarrow{c}=\frac{\mathrm{117}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{\sqrt{\mathrm{1}+\mathrm{6}{x}}−\frac{\mathrm{1}}{\sqrt{\mathrm{1}−\mathrm{6}{x}}}}{\sqrt{\mathrm{1}+\mathrm{3}{x}}−\frac{\mathrm{1}}{\sqrt{\mathrm{1}−\mathrm{3}{x}}}}=\mathrm{4}+\mathrm{6}{x}+\frac{\mathrm{117}}{\mathrm{2}}{x}^{\mathrm{2}} +{o}\left({x}^{\mathrm{3}} \right) \\ $$

Commented by TawaTawa last updated on 16/Jan/20

Wow, God bless you sir

$$\mathrm{Wow},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by mr W last updated on 16/Jan/20

sir, if you are not only interested in result, but want to learn the general method, try to use taylor series and calculate f(0),f′(0), f′′(0) etc.

$${sir},\:{if}\:{you}\:{are}\:{not}\:{only}\:{interested}\:{in} \\ $$$${result},\:{but}\:{want}\:{to}\:{learn}\:{the}\:{general} \\ $$$${method},\:{try}\:{to}\:{use}\:{taylor}\:{series}\:{and} \\ $$$${calculate}\:{f}\left(\mathrm{0}\right),{f}'\left(\mathrm{0}\right),\:{f}''\left(\mathrm{0}\right)\:{etc}. \\ $$

Commented by TawaTawa last updated on 16/Jan/20

Alright sir. God bless you. But sir, i am a miss.

$$\mathrm{Alright}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}.\: \\ $$$$\mathrm{But}\:\mathrm{sir},\:\:\mathrm{i}\:\mathrm{am}\:\mathrm{a}\:\mathrm{miss}. \\ $$

Commented by peter frank last updated on 17/Jan/20

nice solution.both

$${nice}\:{solution}.{both} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com