how to solve find inf and sup of A 1. A={(m/n)+((4n)/m) m,n ∈N} 2. A={((mn)/(4m^2 + n^2 )) m∈Z,n ∈N} 3. A={(m/(∣m∣ + n)) m∈Z,n ∈N}


Question and Answers Forum

All Questions Topic List
None Questions
Previous in All Question Next in All Question
Previous in None Next in None
Question Number 78425 by arkanmath7@gmail.com last updated on 17/Jan/20
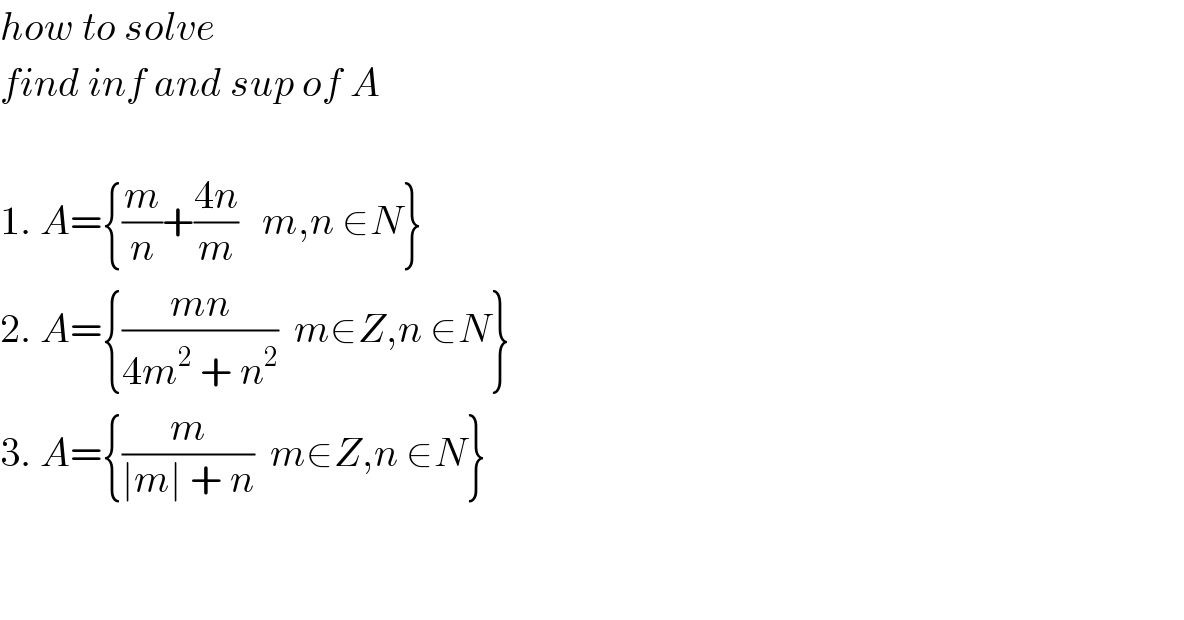
$how to solve find inf and sup of A 1. A={(m/n)+((4n)/m) m,n ∈N} 2. A={((mn)/(4m^2 + n^2 )) m∈Z,n ∈N} 3. A={(m/(∣m∣ + n)) m∈Z,n ∈N}$
$h o w t o s o l v e$ $f i n d i n f a n d s u p o f A$ $1 . A = {\frac{m}{n} + \frac{4 n}{m} m, n \in N}$ $2 . A = {\frac{m n}{4 m^{2} + n^{2}} m \in Z, n \in N}$ $3 . A = {\frac{m}{∣ m ∣ + n} m \in Z, n \in N}$
	Answered by MJS last updated on 17/Jan/20
	$(d/dm)[(m/n)+((4n)/m)]=(1/n)−((4n)/m^2 )=0 ⇒ m=±2n (d^2 /dm^2 )[(m/n)+((4n)/m)]=((8n)/m^3 )= { ((−(1/n^2 ); m=−2n)),(((1/n^2 ); m=+2n)) :} local max at m=−2n but m, n ∈N ⇒ ⇒ A_(max) =+∞ [m=1∧n→+∞ or n=1∧m→+∞ ⇒ A→+∞] local min at m=2n∧m, n ∈N ⇒ A_(min) =4$
	$\frac{d}{d m} [\frac{m}{n} + \frac{4 n}{m}] = \frac{1}{n} - \frac{4 n}{m^{2}} = 0 \Rightarrow m = \pm 2 n$ $\frac{d^{2}}{{d m}^{2}} [\frac{m}{n} + \frac{4 n}{m}] = \frac{8 n}{m^{3}} = {\begin{cases} - \frac{1}{n^{2}}; m = - 2 n \\ \frac{1}{n^{2}}; m = + 2 n \end{cases}$ $local \max at m = - 2 n but m, n \in N \Rightarrow$ $\Rightarrow A_{\max} = + \infty [m = 1 \land n \to + \infty or n = 1 \land m \to + \infty \Rightarrow A \to + \infty]$ $local \min at m = 2 n \land m, n \in N \Rightarrow A_{\min} = 4$
	Commented by MJS last updated on 17/Jan/20

	$because at a \max the 2^{nd} derivate is smaller$ $than 0$
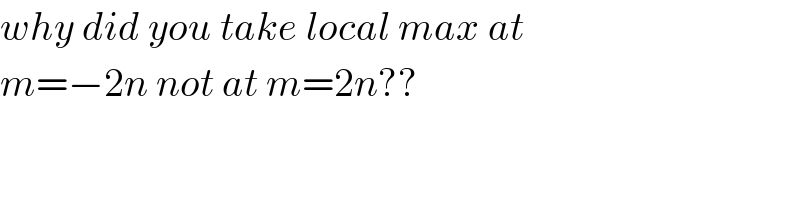
	Commented by arkanmath7@gmail.com last updated on 17/Jan/20

	$w h y d i d y o u t a k e l o c a l m a x a t$ $m = - 2 n n o t a t m = 2 n ? ?$
	Commented by arkanmath7@gmail.com last updated on 17/Jan/20

	$t h a n k y o u s o m u c h s i r$
	Answered by MJS last updated on 17/Jan/20
	$(d/dm)[((mn)/(4m^2 +n^2 ))]=−((n(4m^2 −n^2 ))/((4m^2 +n^2 )^2 ))=0 ⇒ m=±(n/2) (d^2 /dm^2 )[((mn)/(4m^2 +n^2 ))]=((8mn(4m^2 −3n^2 ))/((4m^2 +n^2 )^3 ))= { (((1/n^2 ); m=−(n/2))),((−(1/n^2 ); m=(n/2))) :} min at m=−(n/2); A=−(1/4) max at m=(n/2); A=(1/4) try ((mn)/(4m^2 +n^2 ))<−(1/4) 4mn<−4m^2 −n^2 4m^2 +4mn+n^2 <0 (2m+n)^2 <0 false ((mn)/(4m^2 +n^2 ))>(1/4) leads to (2m−n)^2 <0 ⇒ false$
	$\frac{d}{d m} [\frac{m n}{4 m^{2} + n^{2}}] = - \frac{n (4 m^{2} - n^{2})}{{(4 m^{2} + n^{2})}^{2}} = 0 \Rightarrow m = \pm \frac{n}{2}$ $\frac{d^{2}}{{d m}^{2}} [\frac{m n}{4 m^{2} + n^{2}}] = \frac{8 m n (4 m^{2} - 3 n^{2})}{{(4 m^{2} + n^{2})}^{3}} = {\begin{cases} \frac{1}{n^{2}}; m = - \frac{n}{2} \\ - \frac{1}{n^{2}}; m = \frac{n}{2} \end{cases}$ $\min at m = - \frac{n}{2}; A = - \frac{1}{4}$ $\max at m = \frac{n}{2}; A = \frac{1}{4}$ $try$ $\frac{m n}{4 m^{2} + n^{2}} < - \frac{1}{4}$ $4 m n < - 4 m^{2} - n^{2}$ $4 m^{2} + 4 m n + n^{2} < 0$ ${(2 m + n)}^{2} < 0 false$ $\frac{m n}{4 m^{2} + n^{2}} > \frac{1}{4} leads to {(2 m - n)}^{2} < 0 \Rightarrow false$
	Answered by MJS last updated on 17/Jan/20

	$- 1 < \frac{m}{∣ m ∣ + n} < + 1$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum