
Question and Answers Forum
Question Number 78490 by ~blr237~ last updated on 18/Jan/20
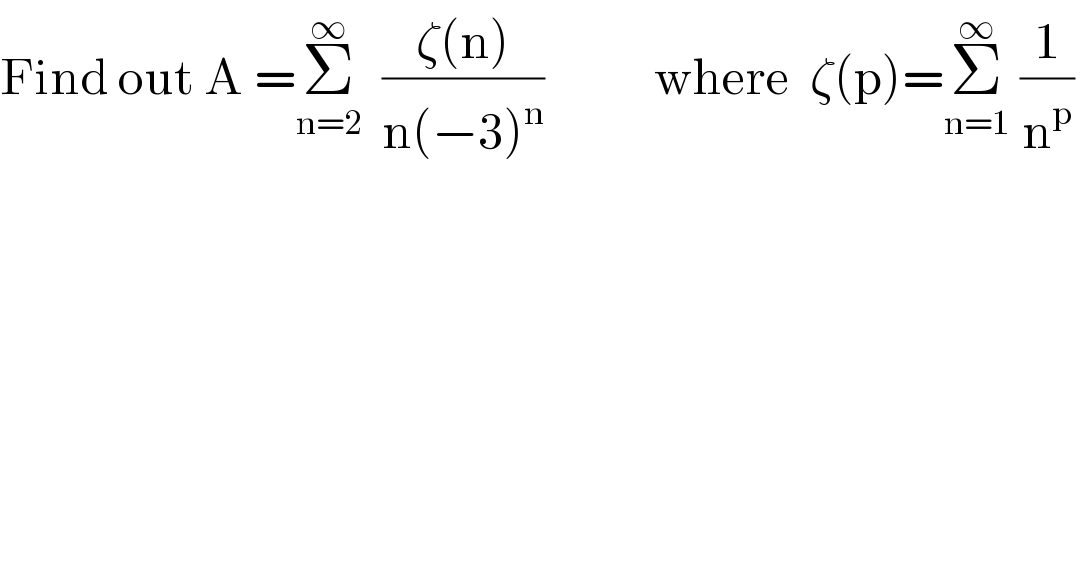
Answered by mind is power last updated on 19/Jan/20
![let f(x)=Σ_(n≥2) ((ζ(n)x^n )/n)=Σ_(n≥2) (x^n /n)Σ_(m≥1) (1/m^n ) =Σ_(n≥2) .Σ_(m≥1) ((x/m))^n .(1/n) ∀n,m ,n≥2 and m≥1 we haveΣ_(n≥2) Σ_(m≥1) ((x/m))^n .(1/n),≤Σ_(n≥2) (x^n /n).ζ(2)<∞ ,∀x∈]−1,1[ ⇒Σ_(n≥2) .Σ_(m≥1) ((x/m))^n .(1/n)=Σ_(m≥1) Σ_(n≥2) ((((x/m))^n )/n)=f(x) Σ_(k≥1) (a^k /k)=−ln(1−a)⇒Σ_(k≥2) (a^k /k)=−ln(1−a)−a f(x)=Σ_(m≥1) {−ln(1−(x/m))−(x/m)}=f(x) we have our sum=f(−(1/3)) Γ(x)=(1/x)Π_(k≥1) (((1+(1/k))^x )/(1+(x/k)))⇒(1/x)Π_(k≥1) .(e^(xln(1+(1/k))) /(1+(x/k)))=(1/x).Π_(k≥1) (e^(xln(1+(1/k))−(x/k)+(x/k)) /(1+(x/k))) =(1/x).Π_(k≥1) (e^(x(ln(1+(1/k))−(1/k))+(x/k)) /(1+(x/k)))=(1/x).e^(Σ_(k≥1) x(ln(1+(1/k))−(1/k))) .Π_(k≥1) (e^(x/k) /e^(ln(1+(x/k))) ) Σ_(k≥1) {ln(1+(1/k))−(1/k)}=−γ Euler macheronie Constent Γ(x)=(e^(−γx) /x).e^(Σ_(k≥1) {(x/k)−ln(1+(x/k))}) ⇒lnΓ(x)=−γx−ln(x)+Σ_(k≥1) {(x/k)−ln(1+(x/k))} ⇒Σ_(k≥1) {(x/k)−ln(1+(x/k))}=ln(Γ(x))+γx+ln(x) ⇒Σ_(k≥1) {−(x/k)−ln(1−(x/k))}=f(x)=ln(Γ(−x))−γx+ln(−x) S=f(−(1/3))=ln(Γ((1/3)))+(γ/3)+ln((1/3))=Σ_(n≥2) ((ζ(n))/(n(−3)^n ))](Q78666.png)
| ||
Question and Answers Forum | ||
Question Number 78490 by ~blr237~ last updated on 18/Jan/20 | ||
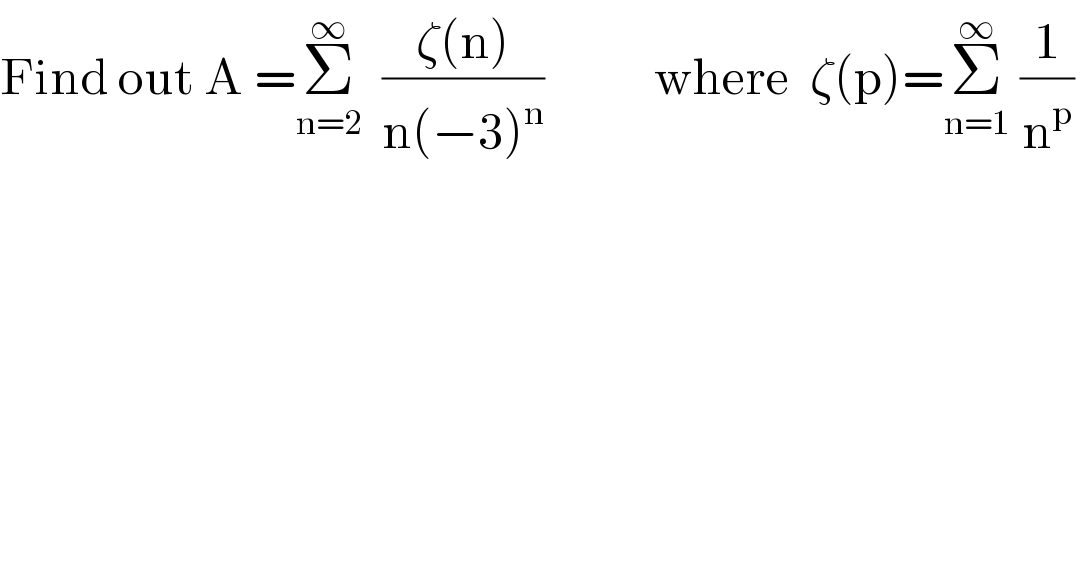 | ||
Answered by mind is power last updated on 19/Jan/20 | ||
![let f(x)=Σ_(n≥2) ((ζ(n)x^n )/n)=Σ_(n≥2) (x^n /n)Σ_(m≥1) (1/m^n ) =Σ_(n≥2) .Σ_(m≥1) ((x/m))^n .(1/n) ∀n,m ,n≥2 and m≥1 we haveΣ_(n≥2) Σ_(m≥1) ((x/m))^n .(1/n),≤Σ_(n≥2) (x^n /n).ζ(2)<∞ ,∀x∈]−1,1[ ⇒Σ_(n≥2) .Σ_(m≥1) ((x/m))^n .(1/n)=Σ_(m≥1) Σ_(n≥2) ((((x/m))^n )/n)=f(x) Σ_(k≥1) (a^k /k)=−ln(1−a)⇒Σ_(k≥2) (a^k /k)=−ln(1−a)−a f(x)=Σ_(m≥1) {−ln(1−(x/m))−(x/m)}=f(x) we have our sum=f(−(1/3)) Γ(x)=(1/x)Π_(k≥1) (((1+(1/k))^x )/(1+(x/k)))⇒(1/x)Π_(k≥1) .(e^(xln(1+(1/k))) /(1+(x/k)))=(1/x).Π_(k≥1) (e^(xln(1+(1/k))−(x/k)+(x/k)) /(1+(x/k))) =(1/x).Π_(k≥1) (e^(x(ln(1+(1/k))−(1/k))+(x/k)) /(1+(x/k)))=(1/x).e^(Σ_(k≥1) x(ln(1+(1/k))−(1/k))) .Π_(k≥1) (e^(x/k) /e^(ln(1+(x/k))) ) Σ_(k≥1) {ln(1+(1/k))−(1/k)}=−γ Euler macheronie Constent Γ(x)=(e^(−γx) /x).e^(Σ_(k≥1) {(x/k)−ln(1+(x/k))}) ⇒lnΓ(x)=−γx−ln(x)+Σ_(k≥1) {(x/k)−ln(1+(x/k))} ⇒Σ_(k≥1) {(x/k)−ln(1+(x/k))}=ln(Γ(x))+γx+ln(x) ⇒Σ_(k≥1) {−(x/k)−ln(1−(x/k))}=f(x)=ln(Γ(−x))−γx+ln(−x) S=f(−(1/3))=ln(Γ((1/3)))+(γ/3)+ln((1/3))=Σ_(n≥2) ((ζ(n))/(n(−3)^n ))](Q78666.png) | ||
| ||