
Question and Answers Forum
Question Number 78596 by jagoll last updated on 19/Jan/20
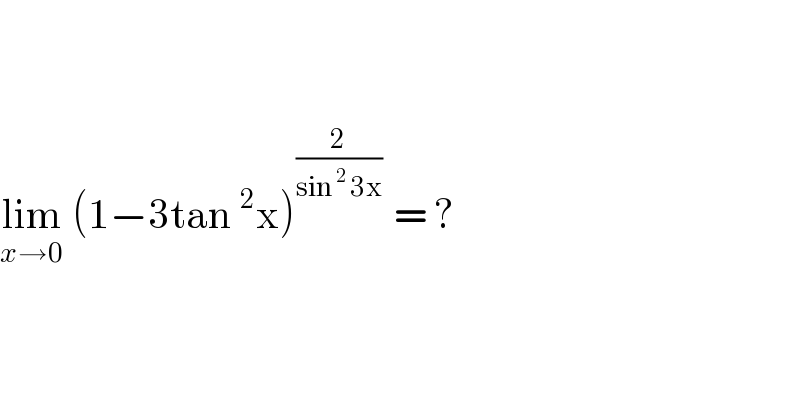
Commented by mathmax by abdo last updated on 19/Jan/20

Answered by john santu last updated on 19/Jan/20
![we know that lim_(x→0) (1+x)^(1/x) = e now we work the question lim_(x→0) [ (1+(−3tan^2 x))^(1/(−3tan^2 x)) ]^((−6tan^2 x)/(sin^2 3x)) = e^(lim_(x→0) (((−6tan^2 x)/(sin^2 3x)))) = e^(−(6/9)) = (1/(e^2 )^(1/(3 )) ) .](Q78597.png)
| ||
Question and Answers Forum | ||
Question Number 78596 by jagoll last updated on 19/Jan/20 | ||
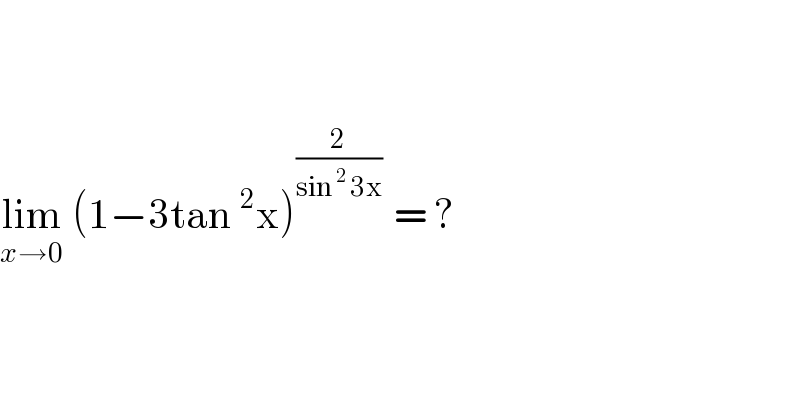 | ||
Commented by mathmax by abdo last updated on 19/Jan/20 | ||
 | ||
Answered by john santu last updated on 19/Jan/20 | ||
![we know that lim_(x→0) (1+x)^(1/x) = e now we work the question lim_(x→0) [ (1+(−3tan^2 x))^(1/(−3tan^2 x)) ]^((−6tan^2 x)/(sin^2 3x)) = e^(lim_(x→0) (((−6tan^2 x)/(sin^2 3x)))) = e^(−(6/9)) = (1/(e^2 )^(1/(3 )) ) .](Q78597.png) | ||
| ||