Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 7861 by Yozzia last updated on 21/Sep/16

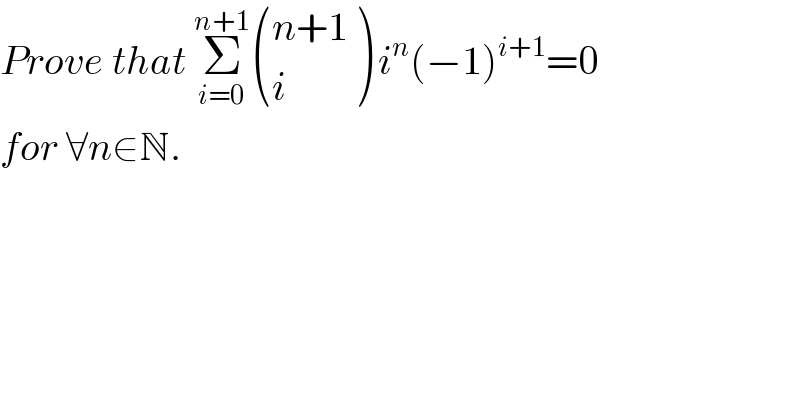
Prove that Σ_(i=0) ^(n+1) (((n+1)),(i) ) i^n (−1)^(i+1) =0 for ∀n∈N.

$${Prove}\:{that}\:\underset{{i}=\mathrm{0}} {\overset{{n}+\mathrm{1}} {\sum}}\begin{pmatrix}{{n}+\mathrm{1}}\\{{i}}\end{pmatrix}\:{i}^{{n}} \left(−\mathrm{1}\right)^{{i}+\mathrm{1}} =\mathrm{0}\: \\ $$$${for}\:\forall{n}\in\mathbb{N}. \\ $$

Commented by FilupSmith last updated on 22/Sep/16

attempt Σ_(i=0) ^(n+1) (((n+1)),(i) ) =Σ_(i=0) ^k ((k!)/(i!∙(k−i)!))=k!Σ_(i=0) ^k (1/(i!∙(k−i)!)) n+1=k ⇒ n=k−1 Σ_(i=0) ^k S=k!((1/(0!×k!))+(1/(1!×(k−1)!))+(1/(2!×(k−2)!))+...+(1/((k−1)!×1!))+(1/(k!×0!))) ∴Σ_(i=0) ^(n+1) (((n+1)),(i) ) i^n (−1)^(n+1) =Σ_(i=0) ^k Si^(k−1) (−1)^k Σ_(i=0) ^k Si^(k−1) =k!((0^(k−1) /(0!×k!))+(1^(k−1) /(1!×(k−1)!))+(2^(k−1) /(2!×(k−2)!))+...+(((k−1)^(k−1) )/((k−1)!×1!))+(k^(k−1) /(k!×0!))) Σ_(i=0) ^k Si^(k−1) =(0^(k−1) /(0!))+((k×1^(k−1) )/(1!))+((k(k−1)2^(k−1) )/(2!))+((k(k−1)(k−2)3^(k−1) )/(3!))+...+((k(k−1)^(k−1) )/(1!))+(k^(k−1) /(0!)) ∴Σ_(i=0) ^k Si^(k−1) (−1)^k =(0^(k−1) /(0!))+((k×1^(k−1) )/(1!))−((k(k−1)2^(k−1) )/(2!))+((k(k−1)(k−2)3^(k−1) )/(3!))−...+((k(k−1)^(k−1) )/(1!))−(k^(k−1) /(0!)) note: + if previous denominator has a even term ∴ = (0^(k−1) /(0!))+(((k×1^(k−1) )/(1!))+((k(k−1)(k−2)3^(k−1) )/(3!))+...)−(((k(k−1)2^(k−1) )/(2!))+((k(k−1)(k−2)(k−3)4^(k−1) )/(4!))+...) working currently unsure how to continue

$${attempt} \\ $$$$\underset{{i}=\mathrm{0}} {\overset{{n}+\mathrm{1}} {\sum}}\begin{pmatrix}{{n}+\mathrm{1}}\\{{i}}\end{pmatrix}\:=\underset{{i}=\mathrm{0}} {\overset{{k}} {\sum}}\:\frac{{k}!}{{i}!\centerdot\left({k}−{i}\right)!}={k}!\underset{{i}=\mathrm{0}} {\overset{{k}} {\sum}}\:\frac{\mathrm{1}}{{i}!\centerdot\left({k}−{i}\right)!} \\ $$$${n}+\mathrm{1}={k}\:\:\:\Rightarrow\:\:{n}={k}−\mathrm{1} \\ $$$$\underset{{i}=\mathrm{0}} {\overset{{k}} {\sum}}{S}={k}!\left(\frac{\mathrm{1}}{\mathrm{0}!×{k}!}+\frac{\mathrm{1}}{\mathrm{1}!×\left({k}−\mathrm{1}\right)!}+\frac{\mathrm{1}}{\mathrm{2}!×\left({k}−\mathrm{2}\right)!}+...+\frac{\mathrm{1}}{\left({k}−\mathrm{1}\right)!×\mathrm{1}!}+\frac{\mathrm{1}}{{k}!×\mathrm{0}!}\right) \\ $$$$\: \\ $$$$\therefore\underset{{i}=\mathrm{0}} {\overset{{n}+\mathrm{1}} {\sum}}\begin{pmatrix}{{n}+\mathrm{1}}\\{{i}}\end{pmatrix}\:{i}^{{n}} \left(−\mathrm{1}\right)^{{n}+\mathrm{1}} =\underset{{i}=\mathrm{0}} {\overset{{k}} {\sum}}{Si}^{{k}−\mathrm{1}} \left(−\mathrm{1}\right)^{{k}} \\ $$$$\: \\ $$$$\underset{{i}=\mathrm{0}} {\overset{{k}} {\sum}}{Si}^{{k}−\mathrm{1}} ={k}!\left(\frac{\mathrm{0}^{{k}−\mathrm{1}} }{\mathrm{0}!×{k}!}+\frac{\mathrm{1}^{{k}−\mathrm{1}} }{\mathrm{1}!×\left({k}−\mathrm{1}\right)!}+\frac{\mathrm{2}^{{k}−\mathrm{1}} }{\mathrm{2}!×\left({k}−\mathrm{2}\right)!}+...+\frac{\left({k}−\mathrm{1}\right)^{{k}−\mathrm{1}} }{\left({k}−\mathrm{1}\right)!×\mathrm{1}!}+\frac{{k}^{{k}−\mathrm{1}} }{{k}!×\mathrm{0}!}\right) \\ $$$$\underset{{i}=\mathrm{0}} {\overset{{k}} {\sum}}{Si}^{{k}−\mathrm{1}} =\frac{\mathrm{0}^{{k}−\mathrm{1}} }{\mathrm{0}!}+\frac{{k}×\mathrm{1}^{{k}−\mathrm{1}} }{\mathrm{1}!}+\frac{{k}\left({k}−\mathrm{1}\right)\mathrm{2}^{{k}−\mathrm{1}} }{\mathrm{2}!}+\frac{{k}\left({k}−\mathrm{1}\right)\left({k}−\mathrm{2}\right)\mathrm{3}^{{k}−\mathrm{1}} }{\mathrm{3}!}+...+\frac{{k}\left({k}−\mathrm{1}\right)^{{k}−\mathrm{1}} }{\mathrm{1}!}+\frac{{k}^{{k}−\mathrm{1}} }{\mathrm{0}!} \\ $$$$\: \\ $$$$\therefore\underset{{i}=\mathrm{0}} {\overset{{k}} {\sum}}{Si}^{{k}−\mathrm{1}} \left(−\mathrm{1}\right)^{{k}} =\frac{\mathrm{0}^{{k}−\mathrm{1}} }{\mathrm{0}!}+\frac{{k}×\mathrm{1}^{{k}−\mathrm{1}} }{\mathrm{1}!}−\frac{{k}\left({k}−\mathrm{1}\right)\mathrm{2}^{{k}−\mathrm{1}} }{\mathrm{2}!}+\frac{{k}\left({k}−\mathrm{1}\right)\left({k}−\mathrm{2}\right)\mathrm{3}^{{k}−\mathrm{1}} }{\mathrm{3}!}−...+\frac{{k}\left({k}−\mathrm{1}\right)^{{k}−\mathrm{1}} }{\mathrm{1}!}−\frac{{k}^{{k}−\mathrm{1}} }{\mathrm{0}!} \\ $$$$\mathrm{note}:\:\:\:+\:\mathrm{if}\:\mathrm{previous}\:\mathrm{denominator}\:\mathrm{has}\:\mathrm{a}\:\mathrm{even}\:\mathrm{term} \\ $$$$\therefore\:=\:\frac{\mathrm{0}^{{k}−\mathrm{1}} }{\mathrm{0}!}+\left(\frac{{k}×\mathrm{1}^{{k}−\mathrm{1}} }{\mathrm{1}!}+\frac{{k}\left({k}−\mathrm{1}\right)\left({k}−\mathrm{2}\right)\mathrm{3}^{{k}−\mathrm{1}} }{\mathrm{3}!}+...\right)−\left(\frac{{k}\left({k}−\mathrm{1}\right)\mathrm{2}^{{k}−\mathrm{1}} }{\mathrm{2}!}+\frac{{k}\left({k}−\mathrm{1}\right)\left({k}−\mathrm{2}\right)\left({k}−\mathrm{3}\right)\mathrm{4}^{{k}−\mathrm{1}} }{\mathrm{4}!}+...\right) \\ $$$${working} \\ $$$${currently}\:{unsure}\:{how}\:{to}\:{continue} \\ $$

Commented by prakash jain last updated on 01/Oct/16

f(x)=(1−e^x )^(n+1) =−Σ_(i=0) ^(n+1) ^(n+1) C_i e^(ix) (−1)^(i+1) f^n (x)=−Σ_(i=0) ^n ^(n+1) C_i i^n e^(ix) (−1)^(i+1) =required expression at x=0 Also f(x)=(1−e^x )^(n+1) =LHS f ′(x)=−(n+1)(1−e^x )^n (−e^x ) f^2 (x)=−[(n+1)(e^x )(1−e^x )^n −(n+1)ne^x (1−e^x )^(n−1) (−e^x )] ⋮ f^n (0)=0 [∵(1−e^x ) is factor till n^(th) differentiation] hence −Σ_(i=0) ^n ^(n+1) C_i i^n (−1)^(i+1) please check

$${f}\left({x}\right)=\left(\mathrm{1}−{e}^{{x}} \right)^{{n}+\mathrm{1}} \\ $$$$=−\underset{{i}=\mathrm{0}} {\overset{{n}+\mathrm{1}} {\sum}}\:^{{n}+\mathrm{1}} {C}_{{i}} {e}^{{ix}} \left(−\mathrm{1}\right)^{{i}+\mathrm{1}} \\ $$$${f}^{{n}} \left({x}\right)=−\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}\:^{{n}+\mathrm{1}} {C}_{{i}} {i}^{{n}} {e}^{{ix}} \left(−\mathrm{1}\right)^{{i}+\mathrm{1}} =\mathrm{required}\:\mathrm{expression} \\ $$$$\mathrm{at}\:{x}=\mathrm{0} \\ $$$$\mathrm{Also}\:{f}\left({x}\right)=\left(\mathrm{1}−{e}^{{x}} \right)^{{n}+\mathrm{1}} ={LHS} \\ $$$${f}\:'\left({x}\right)=−\left({n}+\mathrm{1}\right)\left(\mathrm{1}−{e}^{{x}} \right)^{{n}} \left(−{e}^{{x}} \right) \\ $$$${f}^{\mathrm{2}} \left({x}\right)=−\left[\left({n}+\mathrm{1}\right)\left({e}^{{x}} \right)\left(\mathrm{1}−{e}^{{x}} \right)^{{n}} −\left({n}+\mathrm{1}\right){ne}^{{x}} \left(\mathrm{1}−{e}^{{x}} \right)^{{n}−\mathrm{1}} \left(−{e}^{{x}} \right)\right] \\ $$$$\vdots \\ $$$${f}^{{n}} \left(\mathrm{0}\right)=\mathrm{0}\:\left[\because\left(\mathrm{1}−{e}^{{x}} \right)\:\mathrm{is}\:\mathrm{factor}\:\mathrm{till}\:{n}^{{th}} {differentiation}\right] \\ $$$$\mathrm{hence} \\ $$$$−\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}\:^{{n}+\mathrm{1}} {C}_{{i}} {i}^{{n}} \left(−\mathrm{1}\right)^{{i}+\mathrm{1}} \\ $$$$\mathrm{please}\:\mathrm{check} \\ $$

Commented by Yozzia last updated on 30/Sep/16

That seems sufficient to show that the equation is true. Nicely done! I like the application of the exponential function and binomial theorem.

$${That}\:{seems}\:{sufficient}\:{to}\:{show}\:{that} \\ $$$${the}\:{equation}\:{is}\:{true}.\:{Nicely}\:{done}! \\ $$$${I}\:{like}\:{the}\:{application}\:{of}\:{the}\:{exponential} \\ $$$${function}\:{and}\:{binomial}\:{theorem}. \\ $$

Answered by prakash jain last updated on 22/Sep/16

n=2 −^3 C_0 .0+1^2 ^3 C_1 −2^2 ^3 C_2 +3^2 ^3 C_3 =−0+3−12+9=0 n=3 −0+1^3 ×^4 C_1 −2^3 ×^4 C_2 +3^3 ×^4 C_3 −4^3 ×^4 C_4 =1×4−8×6+27×4−64 =4−48−108−64=0

$${n}=\mathrm{2} \\ $$$$−\:^{\mathrm{3}} {C}_{\mathrm{0}} .\mathrm{0}+\mathrm{1}^{\mathrm{2}} \:^{\mathrm{3}} {C}_{\mathrm{1}} −\mathrm{2}^{\mathrm{2}} \:^{\mathrm{3}} {C}_{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} \:^{\mathrm{3}} {C}_{\mathrm{3}} \\ $$$$=−\mathrm{0}+\mathrm{3}−\mathrm{12}+\mathrm{9}=\mathrm{0} \\ $$$${n}=\mathrm{3} \\ $$$$−\mathrm{0}+\mathrm{1}^{\mathrm{3}} ×^{\mathrm{4}} {C}_{\mathrm{1}} −\mathrm{2}^{\mathrm{3}} ×^{\mathrm{4}} {C}_{\mathrm{2}} +\mathrm{3}^{\mathrm{3}} ×^{\mathrm{4}} {C}_{\mathrm{3}} −\mathrm{4}^{\mathrm{3}} ×^{\mathrm{4}} {C}_{\mathrm{4}} \\ $$$$=\mathrm{1}×\mathrm{4}−\mathrm{8}×\mathrm{6}+\mathrm{27}×\mathrm{4}−\mathrm{64} \\ $$$$=\mathrm{4}−\mathrm{48}−\mathrm{108}−\mathrm{64}=\mathrm{0} \\ $$

Commented by Yozzia last updated on 22/Sep/16

((3),(0) ) has coefficient 0 for T(n)= (((n+1)),(i) ) i^n (−1)^(n+1) n≥0.

$$\begin{pmatrix}{\mathrm{3}}\\{\mathrm{0}}\end{pmatrix}\:{has}\:{coefficient}\:\mathrm{0}\:{for}\:{T}\left({n}\right)=\begin{pmatrix}{{n}+\mathrm{1}}\\{{i}}\end{pmatrix}\:{i}^{{n}} \left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \:{n}\geqslant\mathrm{0}. \\ $$

Commented by Yozzia last updated on 22/Sep/16

I met this series in proving by induction that the general coefficient a_n of the terms in the power series of the W−Lambert function is a_n =(((−1)^(n+1) n^(n−2) )/((n−1)!)), n≥1 W(x)=Σ_(n=1) ^∞ (((−1)^(n+1) n^(n−2) x^n )/((n−1)!)) {−1≤x≤1} W(x)=f^(−1) (xe^x ) for −1≤x≤1.

$${I}\:{met}\:{this}\:{series}\:{in}\:{proving}\:{by}\:{induction}\:{that} \\ $$$${the}\:{general}\:{coefficient}\:{a}_{{n}} \:{of}\:{the}\:{terms}\:{in}\:{the}\:{power}\:{series} \\ $$$${of}\:{the}\:{W}−{Lambert}\:{function}\:{is} \\ $$$${a}_{{n}} =\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {n}^{{n}−\mathrm{2}} }{\left({n}−\mathrm{1}\right)!},\:{n}\geqslant\mathrm{1} \\ $$$${W}\left({x}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {n}^{{n}−\mathrm{2}} {x}^{{n}} }{\left({n}−\mathrm{1}\right)!}\:\:\:\left\{−\mathrm{1}\leqslant{x}\leqslant\mathrm{1}\right\} \\ $$$${W}\left({x}\right)={f}^{−\mathrm{1}} \left({xe}^{{x}} \right)\:\:{for}\:−\mathrm{1}\leqslant{x}\leqslant\mathrm{1}. \\ $$

Commented by prakash jain last updated on 22/Sep/16

Ok my mistake will look at again.

$$\mathrm{Ok}\:\mathrm{my}\:\mathrm{mistake}\:\mathrm{will}\:\mathrm{look}\:\mathrm{at}\:\mathrm{again}. \\ $$

Commented by FilupSmith last updated on 22/Sep/16

This is too complicated. I don′t know much about the W−Function

$$\mathrm{This}\:\mathrm{is}\:\mathrm{too}\:\mathrm{complicated}.\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{know} \\ $$$$\mathrm{much}\:\mathrm{about}\:\mathrm{the}\:{W}−{Function} \\ $$

Commented by prakash jain last updated on 22/Sep/16

n=3 not zero.

$${n}=\mathrm{3}\:{not}\:{zero}. \\ $$

Commented by Yozzia last updated on 22/Sep/16

Check that 3^3 term.

$${Check}\:{that}\:\mathrm{3}^{\mathrm{3}} \:{term}. \\ $$

Commented by prakash jain last updated on 30/Sep/16

Please check answer in comment.

$$\mathrm{Please}\:\mathrm{check}\:\mathrm{answer}\:\mathrm{in}\:\mathrm{comment}.\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com