Question and Answers Forum
Question Number 78694 by TawaTawa last updated on 19/Jan/20
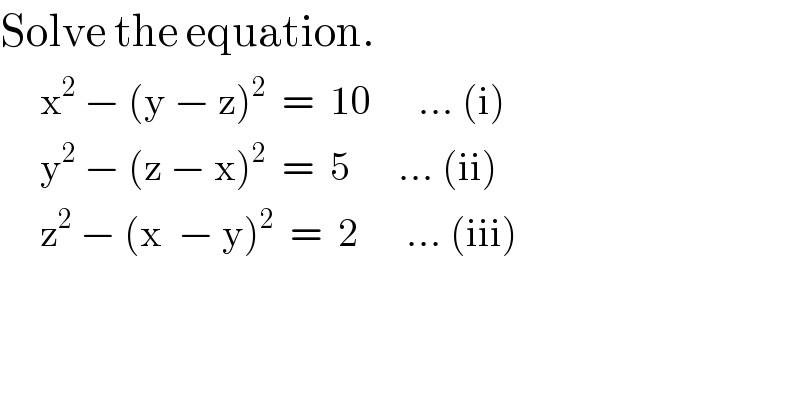
Commented by john santu last updated on 20/Jan/20
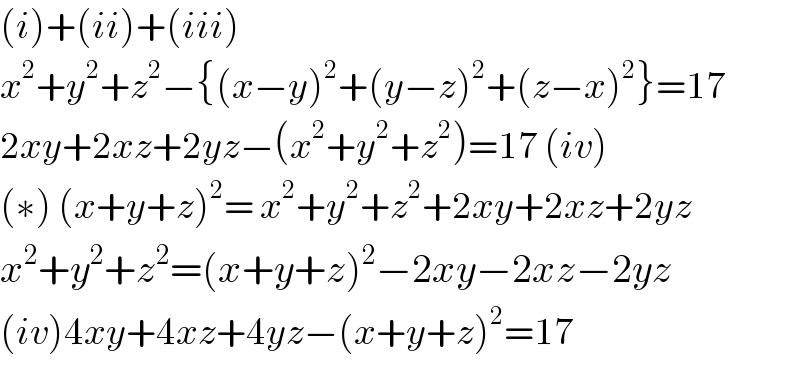
Commented by TawaTawa last updated on 20/Jan/20

Answered by Rasheed.Sindhi last updated on 20/Jan/20
![x^2 − (y − z)^2 = 10 ... (A) y^2 − (z − x)^2 = 5 ... (B) z^2 − (x − y)^2 = 2 ... (C) A/B:(((x−y+z)(x+y−z))/((y−z+x)(y+z−x)))=((10)/5)=2 x−y+z=2(y+z−x) x−y+z=2y+2z−2x) 3x−3y−z=0........∗ A/C:(((x−y+z)(x+y−z))/((z−x+y)(z+x−y)))=((10)/2)=5 ((x+y−z)/(z−x+y))=5 x+y−z=5z−5x+5y 6x−4y−6z=0 3x−2y−3z=0.........∗∗ B/C:(((y−z+x)(y+z−x))/((z−x+y)(z+x−y)))=(5/2) 5(z+x−y)=2(y−z+x) 3x−7y+3z=0......∗∗∗ ∗ , ∗∗ & ∗∗∗ are simultaneous linear equations in 3 variables and can be solved easily: [((3x−3y−z=0)),((3x−2y−3z=0)),((3x−7y+3z=0)) ]](Q78719.png)
Commented by TawaTawa last updated on 20/Jan/20

Answered by jagoll last updated on 20/Jan/20

Commented by jagoll last updated on 20/Jan/20

Commented by mr W last updated on 20/Jan/20

Commented by jagoll last updated on 20/Jan/20
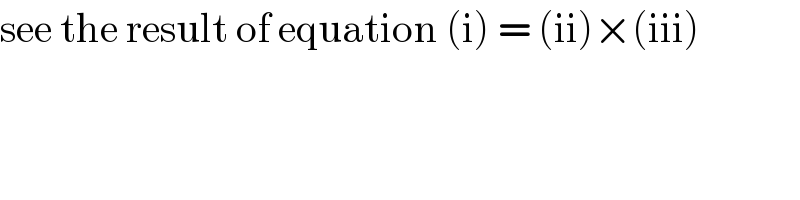
Commented by jagoll last updated on 20/Jan/20
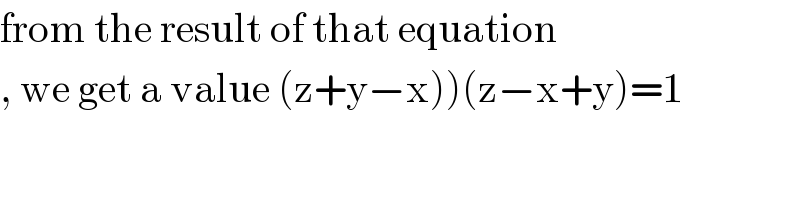
Commented by jagoll last updated on 20/Jan/20
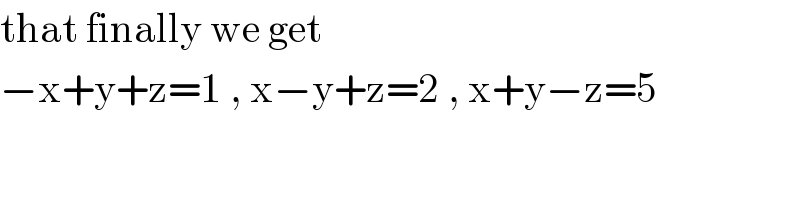
Commented by jagoll last updated on 20/Jan/20

Commented by mr W last updated on 20/Jan/20

Commented by jagoll last updated on 20/Jan/20

Commented by jagoll last updated on 20/Jan/20

Commented by mr W last updated on 20/Jan/20

Commented by jagoll last updated on 20/Jan/20

Commented by mr W last updated on 20/Jan/20

Commented by jagoll last updated on 20/Jan/20

Commented by mr W last updated on 20/Jan/20
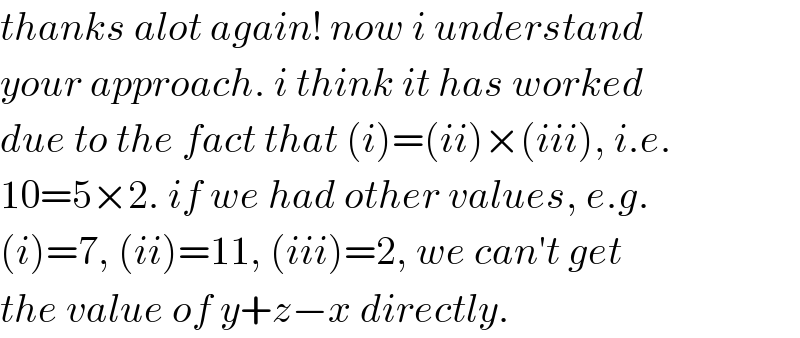
Commented by TawaTawa last updated on 20/Jan/20

Commented by john santu last updated on 21/Jan/20

Commented by john santu last updated on 21/Jan/20

Commented by mr W last updated on 21/Jan/20

Answered by jagoll last updated on 20/Jan/20

Commented by jagoll last updated on 20/Jan/20
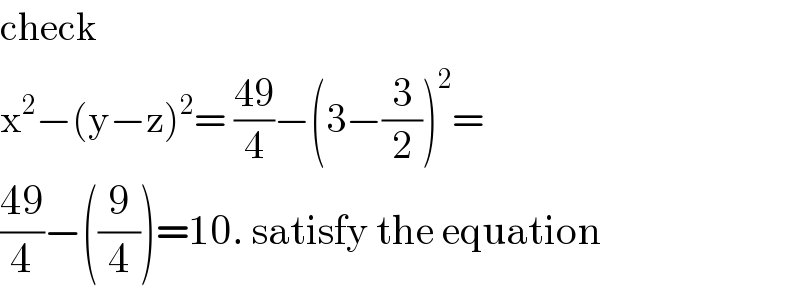
Answered by mr W last updated on 20/Jan/20
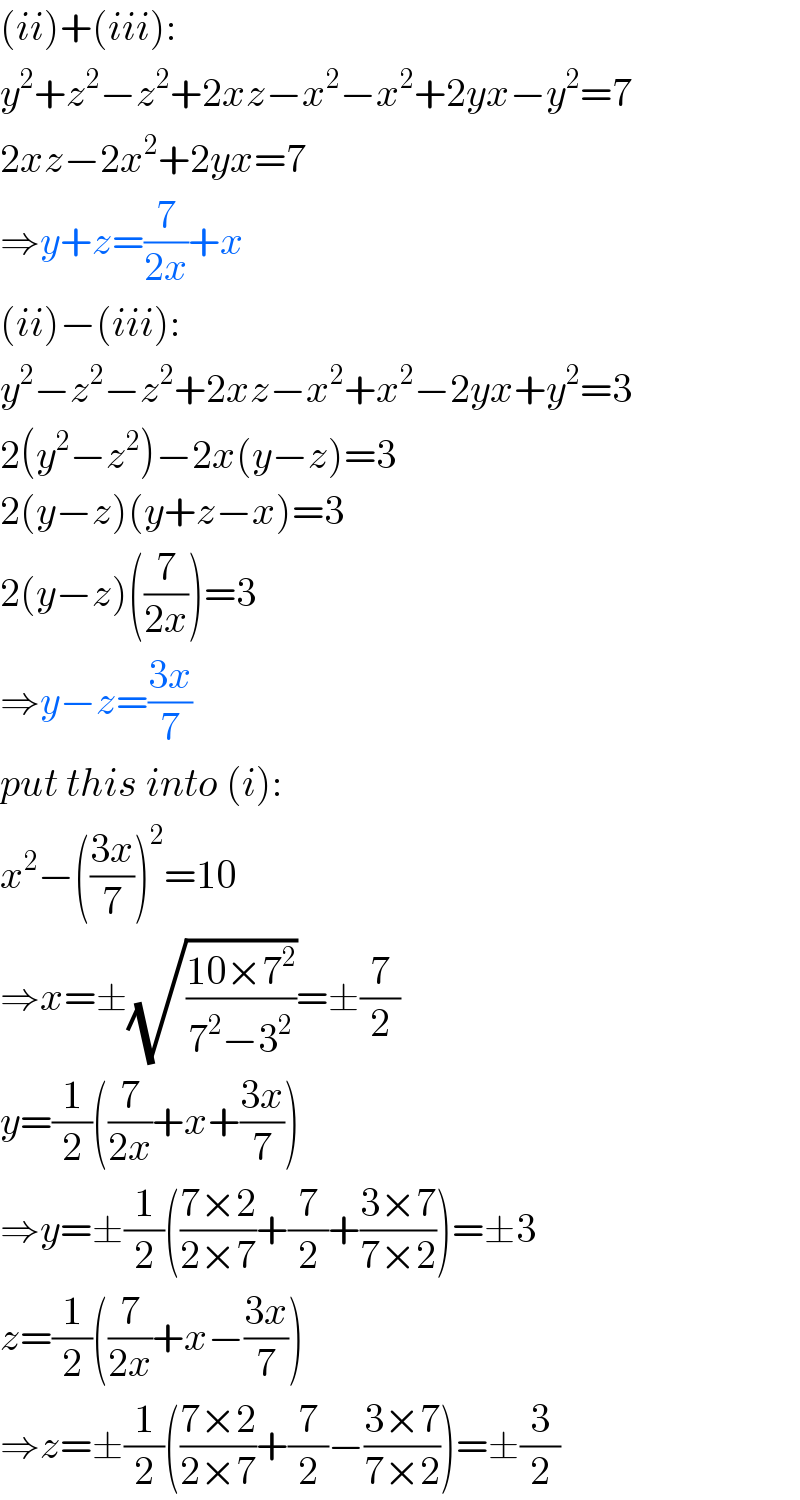
Commented by jagoll last updated on 20/Jan/20
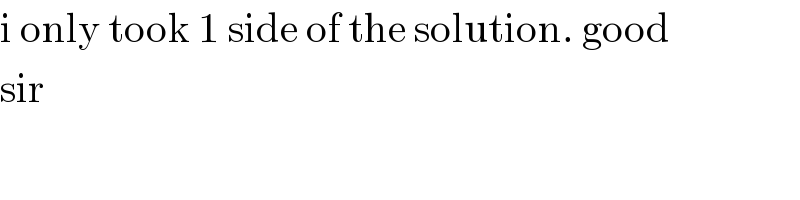
Commented by jagoll last updated on 20/Jan/20

Commented by TawaTawa last updated on 20/Jan/20

Commented by mr W last updated on 20/Jan/20

Commented by TawaTawa last updated on 20/Jan/20
Commented by mr W last updated on 20/Jan/20

Answered by MJS last updated on 20/Jan/20
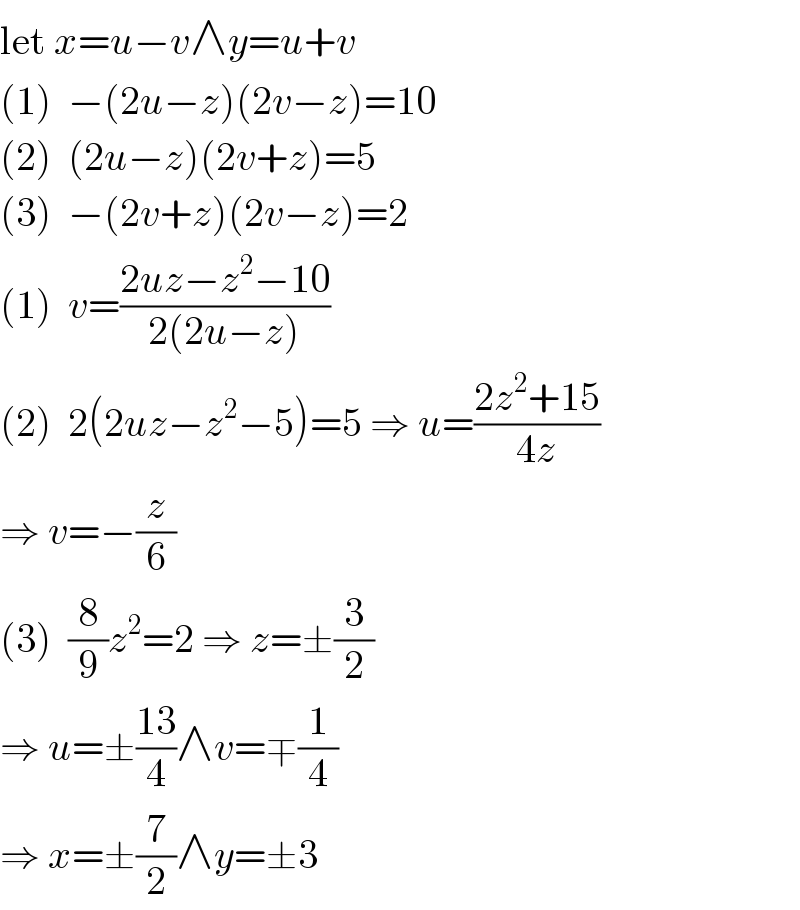
Commented by TawaTawa last updated on 20/Jan/20
Answered by behi83417@gmail.com last updated on 20/Jan/20
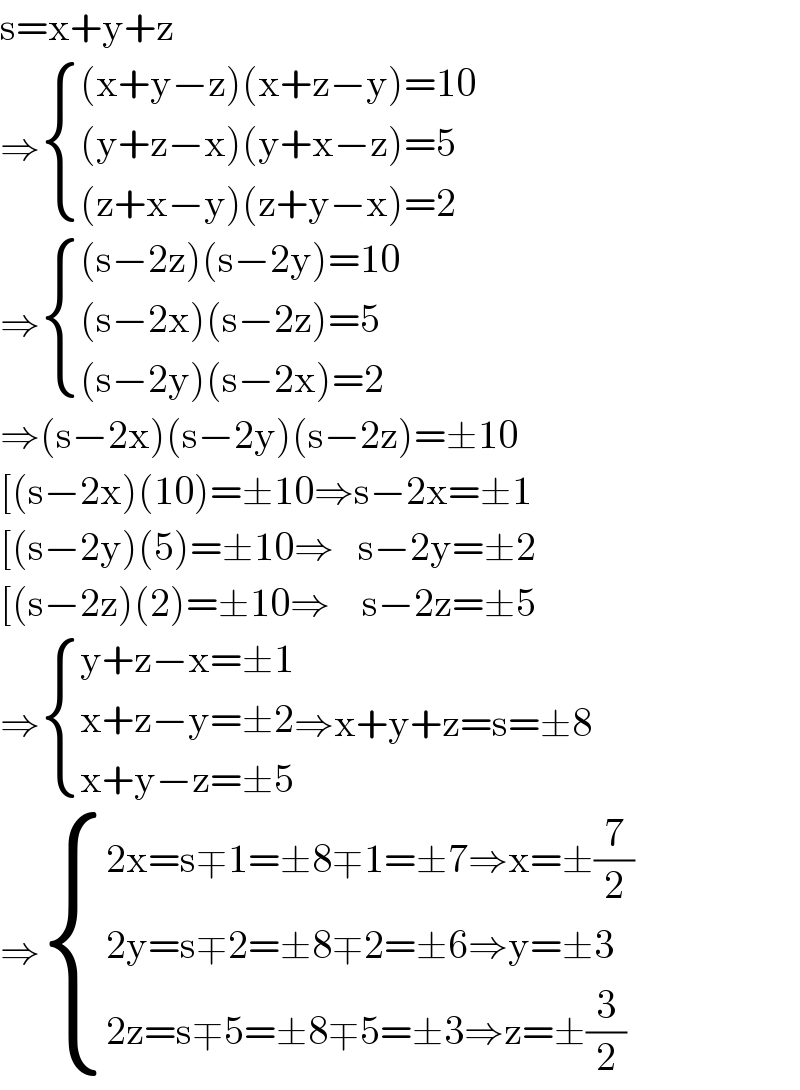
Commented by TawaTawa last updated on 20/Jan/20