
Question and Answers Forum
Question Number 78766 by M±th+et£s last updated on 20/Jan/20
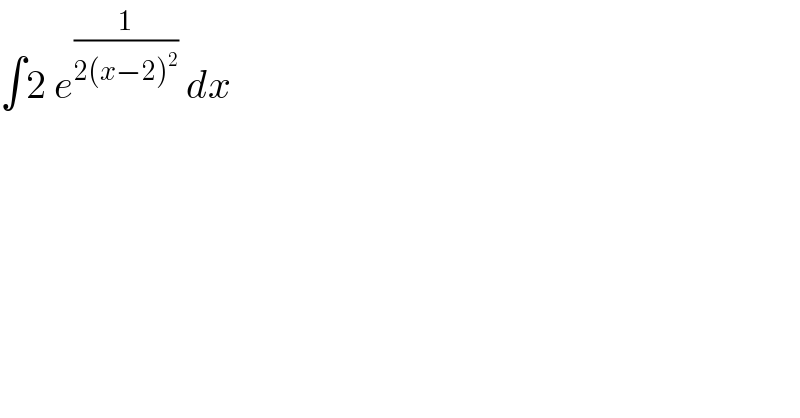
Answered by MJS last updated on 20/Jan/20
![2∫e^(1/(2(x−2)^2 )) dx= [t=2−x → dx=−dt] =−2∫e^(1/(2t^2 )) dt= by parts: u′=1 → u=t v=e^(1/(2t^2 )) → v′=−(e^(1/(2t^2 )) /t^3 ) =−2te^(1/(2t^2 )) +2∫−(e^(1/(2t^2 )) /t^2 )dt= [u=(1/((√2)t)) → dt=−(√2)t^2 du] =−2te^(1/(2t^2 )) +(√(2π))∫((2e^u^2 )/(√π))du= =−2te^(1/(2t^2 )) +(√(2π))erfi u = =−2te^(1/(2t^2 )) +(√(2π))erfi (1/((√2)t))= =−2(2−x)e^(1/(2(2−x)^2 )) +(√(2π))erfi ((√2)/(2(2−x))) +C](Q78782.png)
Commented by mind is power last updated on 20/Jan/20

Commented by M±th+et£s last updated on 20/Jan/20

| ||
Question and Answers Forum | ||
Question Number 78766 by M±th+et£s last updated on 20/Jan/20 | ||
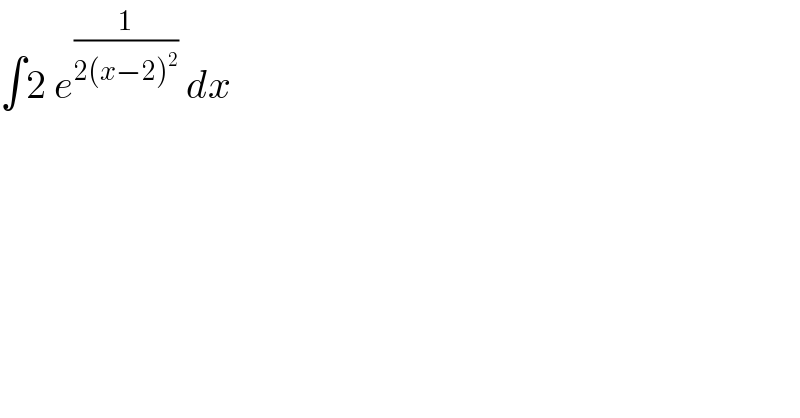 | ||
Answered by MJS last updated on 20/Jan/20 | ||
![2∫e^(1/(2(x−2)^2 )) dx= [t=2−x → dx=−dt] =−2∫e^(1/(2t^2 )) dt= by parts: u′=1 → u=t v=e^(1/(2t^2 )) → v′=−(e^(1/(2t^2 )) /t^3 ) =−2te^(1/(2t^2 )) +2∫−(e^(1/(2t^2 )) /t^2 )dt= [u=(1/((√2)t)) → dt=−(√2)t^2 du] =−2te^(1/(2t^2 )) +(√(2π))∫((2e^u^2 )/(√π))du= =−2te^(1/(2t^2 )) +(√(2π))erfi u = =−2te^(1/(2t^2 )) +(√(2π))erfi (1/((√2)t))= =−2(2−x)e^(1/(2(2−x)^2 )) +(√(2π))erfi ((√2)/(2(2−x))) +C](Q78782.png) | ||
| ||
Commented by mind is power last updated on 20/Jan/20 | ||
 | ||
Commented by M±th+et£s last updated on 20/Jan/20 | ||
 | ||