Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 78767 by jagoll last updated on 20/Jan/20

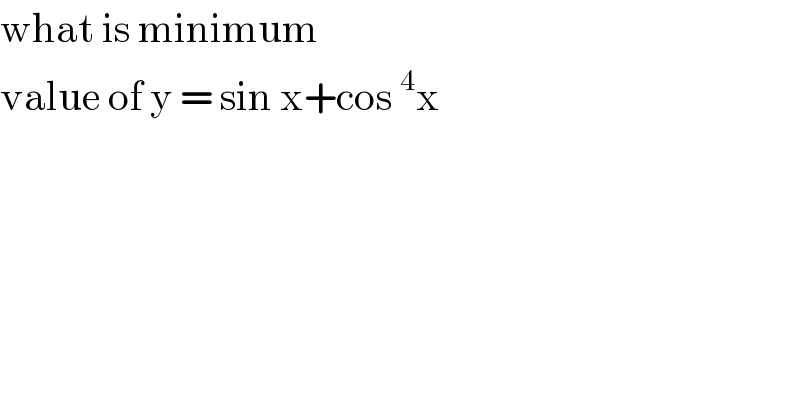
what is minimum value of y = sin x+cos^4 x

$$\mathrm{what}\:\mathrm{is}\:\mathrm{minimum} \\ $$$$\mathrm{value}\:\mathrm{of}\:\mathrm{y}\:=\:\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:^{\mathrm{4}} \mathrm{x} \\ $$

Commented by mr W last updated on 20/Jan/20

since cos^4 x≥0, y_(min) =−1 when sin x=−1 and cos x=0

$${since}\:\mathrm{cos}^{\mathrm{4}} \:{x}\geqslant\mathrm{0}, \\ $$$${y}_{{min}} =−\mathrm{1}\:{when}\:\mathrm{sin}\:{x}=−\mathrm{1}\:{and}\:\mathrm{cos}\:{x}=\mathrm{0} \\ $$

Commented by jagoll last updated on 20/Jan/20

why not use difffential sir?

$$\mathrm{why}\:\mathrm{not}\:\mathrm{use}\:\mathrm{difffential}\:\mathrm{sir}? \\ $$

Commented by jagoll last updated on 20/Jan/20

if the maximum value sir? equal to 1 when cos x = 1 and sin x=0

$$\mathrm{if}\:\mathrm{the}\:\mathrm{maximum}\:\mathrm{value}\:\mathrm{sir}?\:\mathrm{equal}\:\mathrm{to} \\ $$$$\mathrm{1}\:\mathrm{when}\:\mathrm{cos}\:\mathrm{x}\:=\:\mathrm{1}\:\mathrm{and}\:\mathrm{sin}\:\mathrm{x}=\mathrm{0} \\ $$

Commented by mr W last updated on 20/Jan/20

for minimum it is clear: y=sin x+cos^4 x y_(min) is when sin x is minimum which is −1 and at the same time cos^4 x is minimum which is 0. it is possible that at the same time sin x=−1 and cos x=0. for maximum it is not so clear: y=sin x+cos^4 x since both sin x and cos^4 x can be positive, but they can not be 1 at the same time, therefore y_(max) ≠2. cos x=1 and sin x=0 don′t give y=1, but not y_(max) , for example with x=(π/6) we have sin x=(1/2) and cos x=((√3)/2) which give y=(1/2)+(((√3)/2))^4 =1.0625>1. to find where it is the y_(max) we need to do more investigation through y′=0.

$${for}\:{minimum}\:{it}\:{is}\:{clear}: \\ $$$${y}=\mathrm{sin}\:{x}+\mathrm{cos}^{\mathrm{4}} \:{x} \\ $$$${y}_{{min}} \:{is}\:{when}\:{sin}\:{x}\:{is}\:{minimum}\:{which} \\ $$$${is}\:−\mathrm{1}\:{and}\:{at}\:{the}\:{same}\:{time}\:\mathrm{cos}^{\mathrm{4}} \:{x}\:{is}\: \\ $$$${minimum}\:{which}\:{is}\:\mathrm{0}.\:{it}\:{is}\:{possible} \\ $$$${that}\:{at}\:{the}\:{same}\:{time}\:\mathrm{sin}\:{x}=−\mathrm{1}\:{and} \\ $$$$\mathrm{cos}\:{x}=\mathrm{0}. \\ $$$${for}\:{maximum}\:{it}\:{is}\:{not}\:{so}\:{clear}: \\ $$$${y}=\mathrm{sin}\:{x}+\mathrm{cos}^{\mathrm{4}} \:{x} \\ $$$${since}\:{both}\:\mathrm{sin}\:{x}\:{and}\:\mathrm{cos}^{\mathrm{4}} \:{x}\:{can}\:{be} \\ $$$${positive},\:{but}\:{they}\:{can}\:{not}\:{be}\:\mathrm{1}\:{at}\:{the} \\ $$$${same}\:{time},\:{therefore}\:{y}_{{max}} \neq\mathrm{2}. \\ $$$$\mathrm{cos}\:{x}=\mathrm{1}\:{and}\:\mathrm{sin}\:{x}=\mathrm{0}\:{don}'{t}\:{give}\:{y}=\mathrm{1},\:{but} \\ $$$${not}\:{y}_{{max}} ,\:{for}\:{example}\:{with}\:{x}=\frac{\pi}{\mathrm{6}} \\ $$$${we}\:{have}\:\mathrm{sin}\:{x}=\frac{\mathrm{1}}{\mathrm{2}}\:{and}\:\mathrm{cos}\:{x}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:{which} \\ $$$${give}\:{y}=\frac{\mathrm{1}}{\mathrm{2}}+\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{4}} =\mathrm{1}.\mathrm{0625}>\mathrm{1}.\: \\ $$$${to}\:{find}\:{where}\:{it}\:{is}\:{the}\:{y}_{{max}} \:{we}\:{need} \\ $$$${to}\:{do}\:{more}\:{investigation}\:{through} \\ $$$${y}'=\mathrm{0}. \\ $$

Commented by jagoll last updated on 20/Jan/20

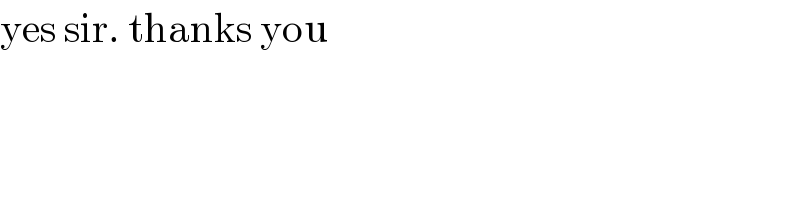
yes sir. thanks you

$$\mathrm{yes}\:\mathrm{sir}.\:\mathrm{thanks}\:\mathrm{you} \\ $$

Commented by mr W last updated on 20/Jan/20

how to find maximum: y=sin x+cos^4 x y′=cos x−4 cos^3 x sin x=0 cos x(1−4 cos^2 x sin x)=0 ⇒cos x=0 ⇒....clear! ⇒sin x=±1 ⇒y_(min) =−1,y=1 ⇒1−4 cos^2 x sin x=0 ⇒1−4 (1−sin^2 x)sin x=0 ⇒sin^3 x−sin x+(1/4)=0 Δ=(−(1/3))^3 +((1/8))^2 <0 ⇒sin x=(2/(√3)) sin ((1/3)sin^(−1) ((3(√3))/8)+((2kπ)/3)) (k=0,1,2) since sin x<1, only k=0 and 1 suitable. k=0: y=1.129515 k=1: y=0.926658 y_(max) =(2/(√3)) sin ((1/3)sin^(−1) ((3(√3))/8))+{1−[(2/(√3)) sin ((1/3)sin^(−1) ((3(√3))/8))]^2 }^2 ≈1.129515

$${how}\:{to}\:{find}\:{maximum}: \\ $$$${y}=\mathrm{sin}\:{x}+\mathrm{cos}^{\mathrm{4}} \:{x} \\ $$$${y}'=\mathrm{cos}\:{x}−\mathrm{4}\:\mathrm{cos}^{\mathrm{3}} \:{x}\:\mathrm{sin}\:{x}=\mathrm{0} \\ $$$$\mathrm{cos}\:{x}\left(\mathrm{1}−\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:{x}\:\mathrm{sin}\:{x}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{cos}\:{x}=\mathrm{0}\:\Rightarrow....{clear}!\:\Rightarrow\mathrm{sin}\:{x}=\pm\mathrm{1}\:\Rightarrow{y}_{{min}} =−\mathrm{1},{y}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{1}−\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:{x}\:\mathrm{sin}\:{x}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{1}−\mathrm{4}\:\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:{x}\right)\mathrm{sin}\:{x}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{sin}^{\mathrm{3}} \:{x}−\mathrm{sin}\:{x}+\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{0} \\ $$$$\Delta=\left(−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{3}} +\left(\frac{\mathrm{1}}{\mathrm{8}}\right)^{\mathrm{2}} <\mathrm{0} \\ $$$$\Rightarrow\mathrm{sin}\:{x}=\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\:\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{8}}+\frac{\mathrm{2}{k}\pi}{\mathrm{3}}\right)\:\:\left({k}=\mathrm{0},\mathrm{1},\mathrm{2}\right) \\ $$$${since}\:\mathrm{sin}\:{x}<\mathrm{1},\:{only}\:{k}=\mathrm{0}\:{and}\:\mathrm{1}\:{suitable}. \\ $$$${k}=\mathrm{0}:\:{y}=\mathrm{1}.\mathrm{129515} \\ $$$${k}=\mathrm{1}:\:{y}=\mathrm{0}.\mathrm{926658} \\ $$$${y}_{{max}} =\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\:\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{8}}\right)+\left\{\mathrm{1}−\left[\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\:\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{8}}\right)\right]^{\mathrm{2}} \right\}^{\mathrm{2}} \\ $$$$\approx\mathrm{1}.\mathrm{129515} \\ $$

Commented by mr W last updated on 20/Jan/20

Commented by jagoll last updated on 20/Jan/20

i had done it like this before : let t= sin x f(t) = t + (1−t^2 )^2 (df/dt) = 1 −4t(1−t^2 )=0 4t^3 −4t+1=0 ⇒ t^3 −t+(1/4)=0 i have trouble with the equation . i forget the cardano formula.

$$\mathrm{i}\:\mathrm{had}\:\mathrm{done}\:\mathrm{it}\:\mathrm{like}\:\mathrm{this}\:\mathrm{before}\::\: \\ $$$$\mathrm{let}\:\mathrm{t}=\:\mathrm{sin}\:\mathrm{x}\: \\ $$$$\mathrm{f}\left(\mathrm{t}\right)\:=\:\mathrm{t}\:+\:\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\frac{\mathrm{df}}{\mathrm{dt}}\:=\:\mathrm{1}\:−\mathrm{4t}\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\mathrm{4t}^{\mathrm{3}} −\mathrm{4t}+\mathrm{1}=\mathrm{0}\:\Rightarrow\:\mathrm{t}^{\mathrm{3}} −\mathrm{t}+\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{0} \\ $$$$\mathrm{i}\:\mathrm{have}\:\mathrm{trouble}\:\mathrm{with}\:\mathrm{the}\:\mathrm{equation} \\ $$$$.\:\mathrm{i}\:\mathrm{forget}\:\mathrm{the}\:\mathrm{cardano}\:\mathrm{formula}. \\ $$$$ \\ $$

Commented by mr W last updated on 20/Jan/20

this leads to the same equation as mine. it has three roots: t=(2/(√3)) sin ((1/3)sin^(−1) ((3(√3))/8)+((2kπ)/3)) (k=0,1,2) but cardano won′t work in this case.

$${this}\:{leads}\:{to}\:{the}\:{same}\:{equation}\:{as}\:{mine}. \\ $$$${it}\:{has}\:{three}\:{roots}: \\ $$$${t}=\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\:\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{8}}+\frac{\mathrm{2}{k}\pi}{\mathrm{3}}\right)\:\:\left({k}=\mathrm{0},\mathrm{1},\mathrm{2}\right) \\ $$$${but}\:{cardano}\:{won}'{t}\:{work}\:{in}\:{this}\:{case}. \\ $$

Commented by mr W last updated on 20/Jan/20

and your approach has a problem: (df/dt)=0 ⇒ means only at t=? f is max. or min. but we want to know at x=? f is max. or min. correct is therefore (df/dx)=0 ⇒(df/dx)=(df/dt)×(dt/dx)=0 ⇒(df/dt)=0 or (dt/dx)=0 (dt/dx)=0 is vanished in your approach which means cos x=0, ⇒ y=1 or y=−1=y_(min) .

$${and}\:{your}\:{approach}\:{has}\:{a}\:{problem}: \\ $$$$\frac{{df}}{{dt}}=\mathrm{0}\:\Rightarrow\:{means}\:{only}\:{at}\:{t}=?\:{f}\:{is}\:{max}.\:{or} \\ $$$${min}. \\ $$$${but}\:{we}\:{want}\:{to}\:{know}\:{at}\:{x}=?\:{f}\:{is}\:{max}. \\ $$$${or}\:{min}. \\ $$$${correct}\:{is}\:{therefore}\:\frac{{df}}{{dx}}=\mathrm{0} \\ $$$$\Rightarrow\frac{{df}}{{dx}}=\frac{{df}}{{dt}}×\frac{{dt}}{{dx}}=\mathrm{0}\:\Rightarrow\frac{{df}}{{dt}}=\mathrm{0}\:{or}\:\frac{{dt}}{{dx}}=\mathrm{0} \\ $$$$\frac{{dt}}{{dx}}=\mathrm{0}\:{is}\:{vanished}\:{in}\:{your}\:{approach} \\ $$$${which}\:{means}\:\mathrm{cos}\:{x}=\mathrm{0},\:\Rightarrow\:{y}=\mathrm{1}\:{or} \\ $$$${y}=−\mathrm{1}={y}_{{min}} . \\ $$

Commented by jagoll last updated on 20/Jan/20

i don′t understand how to get (2/(√3)) sin ((1/3)sin^(−1) (((3(√3))/8))+((2kπ)/3)) sir

$$\mathrm{i}\:\mathrm{don}'\mathrm{t}\:\mathrm{understand}\:\mathrm{how}\:\mathrm{to}\:\mathrm{get}\: \\ $$$$\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\:\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{8}}\right)+\frac{\mathrm{2k}\pi}{\mathrm{3}}\right)\:\mathrm{sir} \\ $$

Commented by jagoll last updated on 20/Jan/20

ow (df/dx)=(df/dt)×(dt/dx) it mean the function we consider two variables?

$$\mathrm{ow}\:\frac{\mathrm{df}}{\mathrm{dx}}=\frac{\mathrm{df}}{\mathrm{dt}}×\frac{\mathrm{dt}}{\mathrm{dx}}\:\mathrm{it}\:\mathrm{mean}\:\mathrm{the}\:\mathrm{function} \\ $$$$\mathrm{we}\:\mathrm{consider}\:\mathrm{two}\:\mathrm{variables}? \\ $$

Commented by mr W last updated on 20/Jan/20

f=t+(1−t^2 )^2 and t=sin x (df/dx)=(df/dt)×(dt/dx)=[1−4t(1−t^2 )]×cos x=0 ⇒cos x=0 or ⇒t^3 −t+(1/4)=0

$${f}={t}+\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} \:{and}\:{t}=\mathrm{sin}\:{x} \\ $$$$\frac{{df}}{{dx}}=\frac{{df}}{{dt}}×\frac{{dt}}{{dx}}=\left[\mathrm{1}−\mathrm{4}{t}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\right]×\mathrm{cos}\:{x}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{cos}\:{x}=\mathrm{0}\:{or} \\ $$$$\Rightarrow{t}^{\mathrm{3}} −{t}+\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com