
Question Number 7883 by 314159 last updated on 23/Sep/16

$${Let}\:{a},{b},{c}\:{be}\:{the}\:{lengths}\:{of}\:{the}\:{sides}\:{of}\:{a}\:{triangle}. \\ $$$${Show}\:{that}\:{abc}\geqslant\left({a}+{b}−{c}\right)\left({b}+{c}−{a}\right)\left({c}+{a}−{b}\right). \\ $$
Commented by sou1618 last updated on 23/Sep/16

$$ \\ $$$${x}={a}+{b}−{c}>\mathrm{0} \\ $$$${y}={c}+{a}−{b}>\mathrm{0}\:\:\:\:{a},{b},{c}\::{length}\:{of}\:{triangle} \\ $$$${z}={b}+{c}−{a}>\mathrm{0} \\ $$$$ \\ $$$${x}+{y}\geqslant\mathrm{2}\sqrt{{xy}}>\mathrm{0} \\ $$$${y}+{z}\geqslant\mathrm{2}\sqrt{{yz}}>\mathrm{0} \\ $$$${z}+{x}\geqslant\mathrm{2}\sqrt{{zx}}>\mathrm{0} \\ $$$$ \\ $$$$\left({x}+{y}\right)\left({y}+{z}\right)\left({z}+{x}\right)\geqslant\mathrm{8}{xyz} \\ $$$$\left(\mathrm{2}{a}\right)×\left(\mathrm{2}{c}\right)×\left(\mathrm{2}{b}\right)\geqslant\mathrm{8}\left({a}+{b}−{c}\right)\left({c}+{a}−{b}\right)\left({b}+{c}−{a}\right) \\ $$$${abc}\geqslant\left({a}+{b}−{c}\right)\left({b}+{c}−{a}\right)\left({c}+{a}−{b}\right)\:. \\ $$
Commented by sou1618 last updated on 23/Sep/16
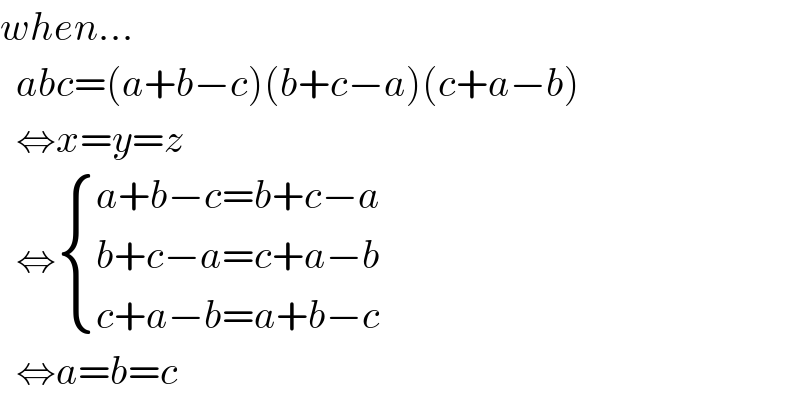
$${when}... \\ $$$$\:\:{abc}=\left({a}+{b}−{c}\right)\left({b}+{c}−{a}\right)\left({c}+{a}−{b}\right) \\ $$$$\:\:\Leftrightarrow{x}={y}={z} \\ $$$$\:\:\Leftrightarrow\begin{cases}{{a}+{b}−{c}={b}+{c}−{a}}\\{{b}+{c}−{a}={c}+{a}−{b}}\\{{c}+{a}−{b}={a}+{b}−{c}}\end{cases} \\ $$$$\:\:\Leftrightarrow{a}={b}={c} \\ $$
Commented by Rasheed Soomro last updated on 23/Sep/16

$$\mathcal{N}{ice}! \\ $$
Answered by prakash jain last updated on 02/Oct/16

$$\mathrm{see}\:\mathrm{comments} \\ $$
