x^3 y′′′ − 3x^2 y′′+6xy′ −6y=x^4 ln(x),x>0


Question and Answers Forum

All Questions Topic List
Differential Equation Questions
Previous in All Question Next in All Question
Previous in Differential Equation Next in Differential Equation
Question Number 78878 by M±th+et£s last updated on 21/Jan/20

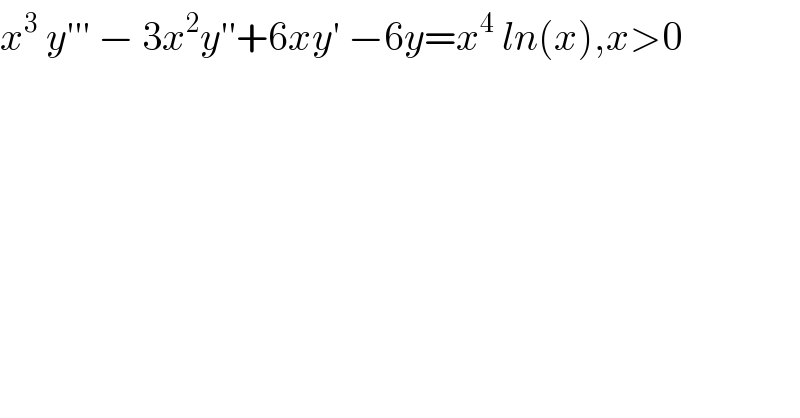
$x^{3} y^{‴} - 3 x^{2} y^{″} + 6 {x y}^{'} - 6 y = x^{4} l n (x), x > 0$
	Answered by mind is power last updated on 21/Jan/20
	$y=x^a Solution of homgenius⇒ x^3 y′′′−3x^2 y′′+6xy′−6y (a(a−1)(a−2)−3a(a−1)+6a−6)y(x)=0 ⇒ (a−1)(a(a−2)−3a+6)=0 (a−1)(a^2 −5a+6)=0 ⇒(a−1)(a−3)(a−2) ⇒a∈{1,2,3} y_1 =x,y_2 =x^2 ,y_3 =x^3 ,y_1 ,y_2 ,y_3 3 independent Solution ⇒ Y=ay_1 +by_2 +cy_3 Solution of Homgenius Equation let y=g(x)x particular Solution y′=xg′+g y′′=2g′+xg′′ y′′′=3g′′+xg′′′ ⇒x^3 (3g′′+xg′′′)−3x^2 (2g′+xg′′)+6x(xg′+g)−6xg(x)=x^4 ln(x) ⇒x^4 g′′′=x^4 ln(x)⇒g′′′(x)=ln(x) ⇒g′′=xln(x)−x g′(x)=((x^2 ln(x))/2)−(x^2 /4)−(x^2 /2)=((x^2 ln(x))/2)−((3x^2 )/4) g(x)=((x^3 ln(x))/6)−(x^3 /(18))−(x^3 /4)=((x^3 ln(x))/6)−((11x^3 )/(36)) y(x)=ax+bx^2 +cx^3 +(x^4 /6)(ln(x)−((11)/6))$
	$y = x^{a} S o l u t i o n o f h o m g e n i u s \Rightarrow$ $x^{3} y^{‴} - 3 x^{2} y^{″} + 6 {x y}^{'} - 6 y$ $(a (a - 1) (a - 2) - 3 a (a - 1) + 6 a - 6) y (x) = 0$ $\Rightarrow$ $(a - 1) (a (a - 2) - 3 a + 6) = 0$ $(a - 1) (a^{2} - 5 a + 6) = 0$ $\Rightarrow (a - 1) (a - 3) (a - 2)$ $\Rightarrow a \in {1, 2, 3}$ $y_{1} = x, y_{2} = x^{2}, y_{3} = x^{3}, y_{1}, y_{2}, y_{3} 3 i n d e p e n d e n t S o l u t i o n \Rightarrow$ $Y = {a y}_{1} + {b y}_{2} + {c y}_{3} S o l u t i o n o f H o m g e n i u s E q u a t i o n$ $l e t y = g (x) x p a r t i c u l a r S o l u t i o n$ $y^{'} = {x g}^{'} + g$ $y^{″} = 2 g^{'} + {x g}^{″}$ $y^{‴} = 3 g^{″} + {x g}^{‴}$ $\Rightarrow x^{3} (3 g^{″} + {x g}^{‴}) - 3 x^{2} (2 g^{'} + {x g}^{″}) + 6 x ({x g}^{'} + g) - 6 x g (x) = x^{4} l n (x)$ $\Rightarrow x^{4} g^{‴} = x^{4} l n (x) \Rightarrow g^{‴} (x) = l n (x)$ $\Rightarrow g^{″} = x l n (x) - x$ $g^{'} (x) = \frac{x^{2} l n (x)}{2} - \frac{x^{2}}{4} - \frac{x^{2}}{2} = \frac{x^{2} l n (x)}{2} - \frac{3 x^{2}}{4}$ $g (x) = \frac{x^{3} l n (x)}{6} - \frac{x^{3}}{18} - \frac{x^{3}}{4} = \frac{x^{3} l n (x)}{6} - \frac{11 x^{3}}{36}$ $y (x) = a x + {b x}^{2} + {c x}^{3} + \frac{x^{4}}{6} (l n (x) - \frac{11}{6})$
	Commented byM±th+et£s last updated on 21/Jan/20

	$g o d b l e s s y o u s i r$
	Commented bymind is power last updated on 21/Jan/20

	$T h a n x y o u T o s i r$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum