Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 79026 by TawaTawa last updated on 22/Jan/20

Commented by mathmax by abdo last updated on 22/Jan/20

we consider the repere (D,DC^→ ,DA^→ ) ⇒D(0,0) ,C(1,0) A(0,1) (1=20cm) ⇒B(1,1) and F((1/2),1) coordonnate of I? M(x,y) ∈ (CF) ⇒det(CM^→ ,CF^→ )=0 ⇒ determinant (((x−1 −(1/2))),((y 1)))=0⇒ (x−1)+(1/2)y=0 ⇒2x−2+y =0 ⇒2x+y−2=0 equation of (BE) E(0,(1/2)) M(x,y) ∈(BE) ⇒det(BM^→ ,BE^→ )=0 ⇒ determinant (((x−1 −1)),((y−1 −(1/2))))=0 ⇒ −(1/2)(x−1)+y−1=0 ⇒(1/2)(x−1)−y+1=0 ⇒x−1−2y+2=0 ⇒ x−2y+1=0 let solve the systeme { ((2x+y−2=0)),((x−2y+1=0 )) :} ⇒ { ((y=−2x+2)),((x−2(−2x+2)+1=0 ⇒ { ((y=−2x+2)),((5x−3=0 ⇒)) :})) :} { ((x=(3/5) ⇒ { ((x=(3/5))),((y=(4/5))) :})),((y=−(6/5)+2 )) :} ⇒ I((3/5),(4/5)) A(BIF)=(1/2)∣det(IF^→ ,IB^→ ) we have IF^→ ((1/2)−(3/5),1−(4/5)) ⇒IF^→ (−(1/(10)),(1/5)) and IB^→ (1−(3/5),1−(4/5)) ⇒IB^→ ((2/5),(1/5)) ⇒ A(BIF) =(1/2)∣ determinant (((−(1/(10)) (2/5))),(((1/5) (1/5))))∣=(1/2)∣(−(1/(50))−(2/(25)))∣ =(1/2)×(5/(50)) =(1/(20)) we have 1 =20 cm ⇒1^2 =20^2 cm^2 ⇒ A(BIF) =(1/(20))×20^2 =20 cm^2 .

$${we}\:{consider}\:{the}\:{repere}\:\left({D},{D}\overset{\rightarrow} {{C}},{D}\overset{\rightarrow} {{A}}\right)\:\Rightarrow{D}\left(\mathrm{0},\mathrm{0}\right)\:,{C}\left(\mathrm{1},\mathrm{0}\right)\:{A}\left(\mathrm{0},\mathrm{1}\right) \\ $$$$\left(\mathrm{1}=\mathrm{20}{cm}\right)\:\Rightarrow{B}\left(\mathrm{1},\mathrm{1}\right)\:\:{and}\:{F}\left(\frac{\mathrm{1}}{\mathrm{2}},\mathrm{1}\right)\:\:{coordonnate}\:{of}\:{I}? \\ $$$${M}\left({x},{y}\right)\:\in\:\left({CF}\right)\:\Rightarrow{det}\left({C}\overset{\rightarrow} {{M}},{C}\overset{\rightarrow} {{F}}\right)=\mathrm{0}\:\Rightarrow\begin{vmatrix}{{x}−\mathrm{1}\:\:\:\:\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{2}}}\\{{y}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{vmatrix}=\mathrm{0}\Rightarrow \\ $$$$\left({x}−\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}}{y}=\mathrm{0}\:\Rightarrow\mathrm{2}{x}−\mathrm{2}+{y}\:=\mathrm{0}\:\Rightarrow\mathrm{2}{x}+{y}−\mathrm{2}=\mathrm{0} \\ $$$${equation}\:{of}\:\left({BE}\right)\:\:\:{E}\left(\mathrm{0},\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$${M}\left({x},{y}\right)\:\in\left({BE}\right)\:\Rightarrow{det}\left({B}\overset{\rightarrow} {{M}}\:,{B}\overset{\rightarrow} {{E}}\right)=\mathrm{0}\:\Rightarrow\begin{vmatrix}{{x}−\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{1}}\\{{y}−\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{2}}}\end{vmatrix}=\mathrm{0}\:\Rightarrow \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\left({x}−\mathrm{1}\right)+{y}−\mathrm{1}=\mathrm{0}\:\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}\left({x}−\mathrm{1}\right)−{y}+\mathrm{1}=\mathrm{0}\:\Rightarrow{x}−\mathrm{1}−\mathrm{2}{y}+\mathrm{2}=\mathrm{0}\:\Rightarrow \\ $$$${x}−\mathrm{2}{y}+\mathrm{1}=\mathrm{0}\:\:\:{let}\:{solve}\:{the}\:{systeme}\:\begin{cases}{\mathrm{2}{x}+{y}−\mathrm{2}=\mathrm{0}}\\{{x}−\mathrm{2}{y}+\mathrm{1}=\mathrm{0}\:}\end{cases} \\ $$$$\:\:\:\:\Rightarrow\begin{cases}{{y}=−\mathrm{2}{x}+\mathrm{2}}\\{{x}−\mathrm{2}\left(−\mathrm{2}{x}+\mathrm{2}\right)+\mathrm{1}=\mathrm{0}\:\Rightarrow\begin{cases}{{y}=−\mathrm{2}{x}+\mathrm{2}}\\{\mathrm{5}{x}−\mathrm{3}=\mathrm{0}\:\Rightarrow}\end{cases}}\end{cases} \\ $$$$\begin{cases}{{x}=\frac{\mathrm{3}}{\mathrm{5}}\:\:\:\:\Rightarrow\:\:\:\:\:\:\:\begin{cases}{{x}=\frac{\mathrm{3}}{\mathrm{5}}}\\{{y}=\frac{\mathrm{4}}{\mathrm{5}}}\end{cases}}\\{{y}=−\frac{\mathrm{6}}{\mathrm{5}}+\mathrm{2}\:}\end{cases} \\ $$$$\Rightarrow\:{I}\left(\frac{\mathrm{3}}{\mathrm{5}},\frac{\mathrm{4}}{\mathrm{5}}\right) \\ $$$${A}\left({BIF}\right)=\frac{\mathrm{1}}{\mathrm{2}}\mid{det}\left({I}\overset{\rightarrow} {{F}},{I}\overset{\rightarrow} {{B}}\right)\:\:\:\:\:{we}\:{have}\:{I}\overset{\rightarrow} {{F}}\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{5}},\mathrm{1}−\frac{\mathrm{4}}{\mathrm{5}}\right) \\ $$$$\Rightarrow{I}\overset{\rightarrow} {{F}}\left(−\frac{\mathrm{1}}{\mathrm{10}},\frac{\mathrm{1}}{\mathrm{5}}\right)\:\:\:\:{and}\:{I}\overset{\rightarrow} {{B}}\left(\mathrm{1}−\frac{\mathrm{3}}{\mathrm{5}},\mathrm{1}−\frac{\mathrm{4}}{\mathrm{5}}\right)\:\Rightarrow{I}\overset{\rightarrow} {{B}}\left(\frac{\mathrm{2}}{\mathrm{5}},\frac{\mathrm{1}}{\mathrm{5}}\right)\:\Rightarrow \\ $$$${A}\left({BIF}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\mid\begin{vmatrix}{−\frac{\mathrm{1}}{\mathrm{10}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{2}}{\mathrm{5}}}\\{\frac{\mathrm{1}}{\mathrm{5}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{5}}}\end{vmatrix}\mid=\frac{\mathrm{1}}{\mathrm{2}}\mid\left(−\frac{\mathrm{1}}{\mathrm{50}}−\frac{\mathrm{2}}{\mathrm{25}}\right)\mid \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{5}}{\mathrm{50}}\:=\frac{\mathrm{1}}{\mathrm{20}}\:\:\:\:\:\:{we}\:{have}\:\mathrm{1}\:=\mathrm{20}\:{cm}\:\Rightarrow\mathrm{1}^{\mathrm{2}} =\mathrm{20}^{\mathrm{2}} {cm}^{\mathrm{2}} \:\Rightarrow \\ $$$${A}\left({BIF}\right)\:=\frac{\mathrm{1}}{\mathrm{20}}×\mathrm{20}^{\mathrm{2}} \:=\mathrm{20}\:{cm}^{\mathrm{2}} . \\ $$

Commented by TawaTawa last updated on 22/Jan/20

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by msup trace by abdo last updated on 22/Jan/20

you are welcome

$${you}\:{are}\:{welcome} \\ $$

Commented by jagoll last updated on 22/Jan/20

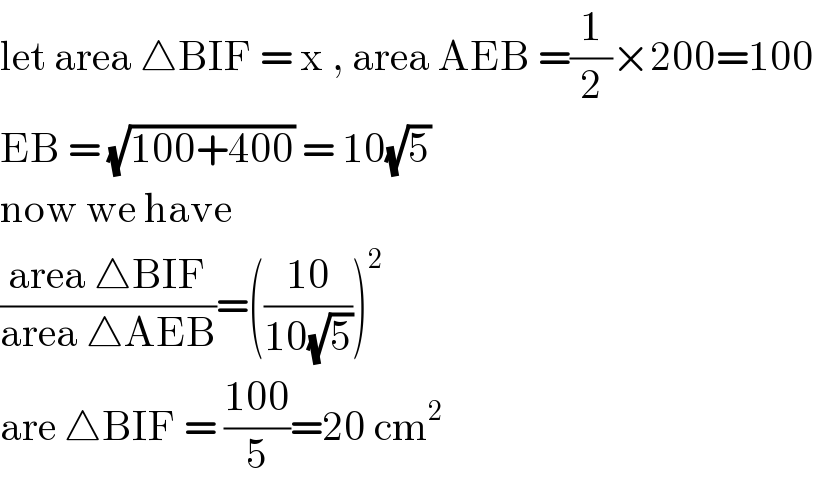
let area △BIF = x , area AEB =(1/2)×200=100 EB = (√(100+400)) = 10(√5) now we have ((area △BIF)/(area △AEB))=(((10)/(10(√5))))^2 are △BIF = ((100)/5)=20 cm^(2 )

$$\mathrm{let}\:\mathrm{area}\:\bigtriangleup\mathrm{BIF}\:=\:\mathrm{x}\:,\:\mathrm{area}\:\mathrm{AEB}\:=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{200}=\mathrm{100} \\ $$$$\mathrm{EB}\:=\:\sqrt{\mathrm{100}+\mathrm{400}}\:=\:\mathrm{10}\sqrt{\mathrm{5}} \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{have}\: \\ $$$$\frac{\mathrm{area}\:\bigtriangleup\mathrm{BIF}}{\mathrm{area}\:\bigtriangleup\mathrm{AEB}}=\left(\frac{\mathrm{10}}{\mathrm{10}\sqrt{\mathrm{5}}}\right)^{\mathrm{2}} \\ $$$$\mathrm{are}\:\bigtriangleup\mathrm{BIF}\:=\:\frac{\mathrm{100}}{\mathrm{5}}=\mathrm{20}\:\mathrm{cm}^{\mathrm{2}\:} \\ $$

Commented by TawaTawa last updated on 23/Jan/20

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by mind is power last updated on 22/Jan/20

first Idea let D(0,0),C(20,0),B(20,20),A(0,20) E(0,10),F(10,20) (EB):y=ax+b a=((10)/(20))=(1/2) y=(x/2)+b,⇒b=20−((20)/2)=10 y=(x/2)+10 CF:y=ax+b,a=−((20)/(10))=−2 y=−2x+b,b=40,y=−2x+40 I=(EB)∩(CF) { ((y=−2x+40)),((y=(x/2)+10)) :} ⇒−2x+40=(x/2)+10 (5/2)x=30⇒x=12,y=16 I(12,16) Area IFB=(1/2)∣Det(IF^→ ,IB^→ )∣ IF^→ =(−2,4),IB^→ (8,4) determinant (((−2 8)),(( 4 4)))=40 Area=((40)/2)=20

$${first}\:{Idea} \\ $$$${let}\:{D}\left(\mathrm{0},\mathrm{0}\right),{C}\left(\mathrm{20},\mathrm{0}\right),{B}\left(\mathrm{20},\mathrm{20}\right),{A}\left(\mathrm{0},\mathrm{20}\right) \\ $$$${E}\left(\mathrm{0},\mathrm{10}\right),{F}\left(\mathrm{10},\mathrm{20}\right) \\ $$$$\left({EB}\right):{y}={ax}+{b}\:\:{a}=\frac{\mathrm{10}}{\mathrm{20}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${y}=\frac{{x}}{\mathrm{2}}+{b},\Rightarrow{b}=\mathrm{20}−\frac{\mathrm{20}}{\mathrm{2}}=\mathrm{10} \\ $$$${y}=\frac{{x}}{\mathrm{2}}+\mathrm{10} \\ $$$${CF}:{y}={ax}+{b},{a}=−\frac{\mathrm{20}}{\mathrm{10}}=−\mathrm{2} \\ $$$${y}=−\mathrm{2}{x}+{b},{b}=\mathrm{40},{y}=−\mathrm{2}{x}+\mathrm{40} \\ $$$${I}=\left({EB}\right)\cap\left({CF}\right)\begin{cases}{{y}=−\mathrm{2}{x}+\mathrm{40}}\\{{y}=\frac{{x}}{\mathrm{2}}+\mathrm{10}}\end{cases} \\ $$$$\Rightarrow−\mathrm{2}{x}+\mathrm{40}=\frac{{x}}{\mathrm{2}}+\mathrm{10} \\ $$$$\frac{\mathrm{5}}{\mathrm{2}}{x}=\mathrm{30}\Rightarrow{x}=\mathrm{12},{y}=\mathrm{16} \\ $$$${I}\left(\mathrm{12},\mathrm{16}\right) \\ $$$${Area}\:{IFB}=\frac{\mathrm{1}}{\mathrm{2}}\mid{Det}\left({I}\overset{\rightarrow} {{F}},{I}\overset{\rightarrow} {{B}}\right)\mid \\ $$$${I}\overset{\rightarrow} {{F}}=\left(−\mathrm{2},\mathrm{4}\right),{I}\overset{\rightarrow} {{B}}\left(\mathrm{8},\mathrm{4}\right) \\ $$$$\begin{vmatrix}{−\mathrm{2}\:\:\:\:\:\:\:\:\mathrm{8}}\\{\:\:\:\:\mathrm{4}\:\:\:\:\:\:\:\:\:\mathrm{4}}\end{vmatrix}=\mathrm{40} \\ $$$${Area}=\frac{\mathrm{40}}{\mathrm{2}}=\mathrm{20} \\ $$

Commented by TawaTawa last updated on 22/Jan/20

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by mr W last updated on 22/Jan/20

Commented by mr W last updated on 22/Jan/20

FG=((AE)/2)=((AD)/4)=((BC)/4) ((HB)/(FB−HB))=((HB)/(FH))=((BC)/(FG))=4 ⇒HB=(4/5)FB=IK ⇒Δ_(IBC) =(4/5)Δ_(FBC) ⇒Δ_(BIF) =Δ_(FBC) −Δ_(IBC) =(1/5)Δ_(FBC) =(1/5)×(([ABCD])/4) =((20×20)/(20))=20 cm^2

$${FG}=\frac{{AE}}{\mathrm{2}}=\frac{{AD}}{\mathrm{4}}=\frac{{BC}}{\mathrm{4}} \\ $$$$\frac{{HB}}{{FB}−{HB}}=\frac{{HB}}{{FH}}=\frac{{BC}}{{FG}}=\mathrm{4} \\ $$$$\Rightarrow{HB}=\frac{\mathrm{4}}{\mathrm{5}}{FB}={IK} \\ $$$$\Rightarrow\Delta_{{IBC}} =\frac{\mathrm{4}}{\mathrm{5}}\Delta_{{FBC}} \\ $$$$\Rightarrow\Delta_{{BIF}} =\Delta_{{FBC}} −\Delta_{{IBC}} =\frac{\mathrm{1}}{\mathrm{5}}\Delta_{{FBC}} =\frac{\mathrm{1}}{\mathrm{5}}×\frac{\left[{ABCD}\right]}{\mathrm{4}} \\ $$$$=\frac{\mathrm{20}×\mathrm{20}}{\mathrm{20}}=\mathrm{20}\:{cm}^{\mathrm{2}} \\ $$

Commented by TawaTawa last updated on 22/Jan/20

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by john santu last updated on 22/Jan/20

Commented by TawaTawa last updated on 22/Jan/20

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by mr W last updated on 22/Jan/20

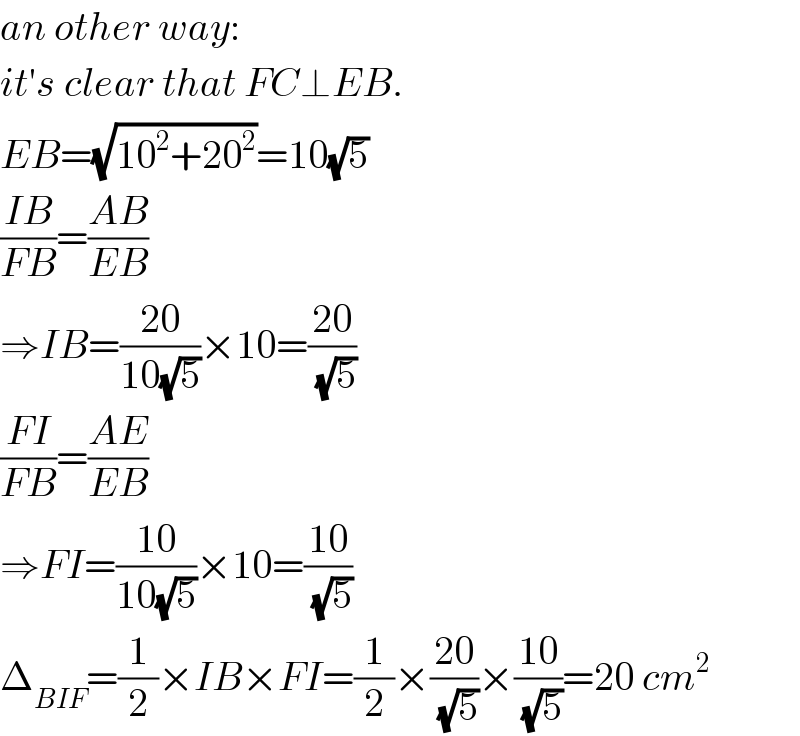
an other way: it′s clear that FC⊥EB. EB=(√(10^2 +20^2 ))=10(√5) ((IB)/(FB))=((AB)/(EB)) ⇒IB=((20)/(10(√5)))×10=((20)/(√5)) ((FI)/(FB))=((AE)/(EB)) ⇒FI=((10)/(10(√5)))×10=((10)/(√5)) Δ_(BIF) =(1/2)×IB×FI=(1/2)×((20)/(√5))×((10)/(√5))=20 cm^2

$${an}\:{other}\:{way}: \\ $$$${it}'{s}\:{clear}\:{that}\:{FC}\bot{EB}. \\ $$$${EB}=\sqrt{\mathrm{10}^{\mathrm{2}} +\mathrm{20}^{\mathrm{2}} }=\mathrm{10}\sqrt{\mathrm{5}} \\ $$$$\frac{{IB}}{{FB}}=\frac{{AB}}{{EB}} \\ $$$$\Rightarrow{IB}=\frac{\mathrm{20}}{\mathrm{10}\sqrt{\mathrm{5}}}×\mathrm{10}=\frac{\mathrm{20}}{\sqrt{\mathrm{5}}} \\ $$$$\frac{{FI}}{{FB}}=\frac{{AE}}{{EB}} \\ $$$$\Rightarrow{FI}=\frac{\mathrm{10}}{\mathrm{10}\sqrt{\mathrm{5}}}×\mathrm{10}=\frac{\mathrm{10}}{\sqrt{\mathrm{5}}} \\ $$$$\Delta_{{BIF}} =\frac{\mathrm{1}}{\mathrm{2}}×{IB}×{FI}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{20}}{\sqrt{\mathrm{5}}}×\frac{\mathrm{10}}{\sqrt{\mathrm{5}}}=\mathrm{20}\:{cm}^{\mathrm{2}} \\ $$

Commented by TawaTawa last updated on 22/Jan/20

God bless you sir. I appreciate

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com